In
geometryGeometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, an
icosidodecahedron is a
polyhedronIn elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon. As such it is one of the
Archimedean solidIn geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
s and more particularly, a
quasiregular polyhedronIn geometry, a quasiregular polyhedron is a semiregular polyhedron that has exactly two kinds of regular faces, which alternate around each vertex. They are edge-transitive and hence step closer to regularity than the semiregular which are merely vertex-transitive.There are only two convex...
.
An icosidodecahedron has icosahedral symmetry, and its first
stellationStellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...
is the compound of a
dodecahedron and its dual
icosahedronIn geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
, with the vertices of the icosahedron located at the midpoints of the edges of either.
Its
dual polyhedronIn geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
is the
rhombic triacontahedronIn geometry, the rhombic triacontahedron is a convex polyhedron with 30 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. It is the polyhedral dual of the icosidodecahedron, and it is a zonohedron....
. An icosidodecahedron can be split along any of six planes to form a pair of
pentagonal rotundaIn geometry, the pentagonal rotunda is one of the Johnson solids . It can be seen as half an icosidodecahedron.The 92 Johnson solids were named and described by Norman Johnson in 1966.-Formulae:...
e, which belong among the
Johnson solidIn geometry, a Johnson solid is a strictly convex polyhedron, each face of which is a regular polygon, but which is not uniform, i.e., not a Platonic solid, Archimedean solid, prism or antiprism. There is no requirement that each face must be the same polygon, or that the same polygons join around...
s.
The icosidodecahedron can be considered a
pentagonal gyrobirotunda, as a combination of two
rotundaeIn geometry, the pentagonal rotunda is one of the Johnson solids . It can be seen as half an icosidodecahedron.The 92 Johnson solids were named and described by Norman Johnson in 1966.-Formulae:...
(compare
pentagonal orthobirotundaIn geometry, the pentagonal orthobirotunda is one of the Johnson solids . As the name suggests, it can be constructed by joining two pentagonal rotundae along their decagonal faces, matching like faces...
, one of the
Johnson solidIn geometry, a Johnson solid is a strictly convex polyhedron, each face of which is a regular polygon, but which is not uniform, i.e., not a Platonic solid, Archimedean solid, prism or antiprism. There is no requirement that each face must be the same polygon, or that the same polygons join around...
s).
The wire frame figure of the icosidodecahedron consists of six
flat regular decagonsIn geometry, a decagon is any polygon with ten sides and ten angles, and usually refers to a regular decagon, having all sides of equal length and each internal angle equal to 144°...
, meeting in pairs at each of the 30 vertices.
In four-dimensional geometry the icosidodecahedron appears in the regular
600-cell as the equatorial slice that belongs to the vertex-first passage of the 600-cell through 3D space. In other words: the 30 vertices of the 600-cell which lie at arc distances of 90 degrees on its circumscribed
hypersphereIn mathematics, an n-sphere is a generalization of the surface of an ordinary sphere to arbitrary dimension. For any natural number n, an n-sphere of radius r is defined as the set of points in -dimensional Euclidean space which are at distance r from a central point, where the radius r may be any...
from a pair of opposite vertices, are the vertices of an icosidodecahedron.
The wire frame figure of the 600-cell consists of 72 flat regular decagons. Six of these are the equatorial decagons to a pair of opposite vertices. They are precisely the six decagons which form the wire frame figure of the icosidodecahedron.
Cartesian coordinates
Convenient Cartesian coordinates for the vertices of an icosidodecahedron with unit edges are given by:
- (0,0,±τ)
- (0,±τ,0)
- (±τ,0,0)
- (±1/2, ±τ/2, ±(1+τ)/2)
- (±τ/2, ±(1+τ)/2, ±1/2)
- (±(1+τ)/2, ±1/2, ±τ/2)
where τ is the
golden ratioIn mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
, (1+√5)/2.
Orthogonal projections
The icosidodecahedron has four special orthogonal projections, centered, on a vertex, an edge, a triangular face, and a pentagonal face. The last two correspond to the A
2 and H
2 Coxeter planes.
Orthogonal projections
| Centered by |
Vertex |
Edge |
Face
Triangle |
Face
Pentagon |
| Image |
|
|
|
|
Projective
symmetry |
[2] |
[2] |
[6] |
[10] |
Surface area and volume
The surface area
A and the volume
V of the icosidodecahedron of edge length
a are:
Related polyhedra
The icosidodecahedron is a
rectifiedIn Euclidean geometry, rectification is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points...
dodecahedron and also a rectified
icosahedronIn geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
, existing as the full-edge truncation between these regular solids.
The Icosidodecahedron contains 12 pentagons of the
dodecahedron and 20 triangles of the
icosahedronIn geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
:
| Picture |
Dodecahedron |
Truncated dodecahedronIn geometry, the truncated dodecahedron is an Archimedean solid. It has 12 regular decagonal faces, 20 regular triangular faces, 60 vertices and 90 edges.- Geometric relations :...
|
IcosidodecahedronIn geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...
|
Truncated icosahedronIn geometry, the truncated icosahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids whose faces are two or more types of regular polygons.It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices and 90 edges....
|
IcosahedronIn geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
|
| Coxeter-Dynkin In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
|
|
|
|
|
|
Pentagonal gyrobirotunda
It is also related to the
Johnson solidIn geometry, a Johnson solid is a strictly convex polyhedron, each face of which is a regular polygon, but which is not uniform, i.e., not a Platonic solid, Archimedean solid, prism or antiprism. There is no requirement that each face must be the same polygon, or that the same polygons join around...
called a
pentagonal orthobirotundaIn geometry, the pentagonal orthobirotunda is one of the Johnson solids . As the name suggests, it can be constructed by joining two pentagonal rotundae along their decagonal faces, matching like faces...
created by two
pentagonal rotundaIn geometry, the pentagonal rotunda is one of the Johnson solids . It can be seen as half an icosidodecahedron.The 92 Johnson solids were named and described by Norman Johnson in 1966.-Formulae:...
connected as mirror images.
(Dissection) |
Icosidodecahedron
(pentagonal gyrobirotunda) |
Pentagonal orthobirotunda |
Pentagonal rotunda |
|
Eight uniform star polyhedra share the same
vertex arrangementIn geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes....
. Of these, two also share the same edge arrangement: the
small icosihemidodecahedronIn geometry, the small icosihemidodecahedron is a uniform star polyhedron, indexed as U49. Its vertex figure alternates two regular triangles and decagons as a crossed quadrilateral....
(having the triangular faces in common), and the
small dodecahemidodecahedronIn geometry, the small dodecahemidodecahedron is a nonconvex uniform polyhedron, indexed as U51. Its vertex figure alternates two regular pentagons and decagons as a crossed quadrilateral....
(having the pentagonal faces in common). The vertex arrangement is also shared with the
compoundsA uniform polyhedron compound is a polyhedral compound whose constituents are identical uniform polyhedra, in an arrangement that is also uniform: the symmetry group of the compound acts transitively on the compound's vertices.The uniform polyhedron compounds were first enumerated by John Skilling...
of
five octahedraThis polyhedron can be seen as either a polyhedral stellation or a compound. This compound was first described by Edmund Hess in 1876.- As a stellation :It is the second stellation of the icosahedron, and given as Wenninger model index 23....
and of
five tetrahemihexahedraA compound of five tetrahemihexahedra is a uniform polyhedron compound and a symmetric arrangement of five tetrahemihexahedra. It is chiral with icosahedral symmetry .- Related polyhedra :...
.
Icosidodecahedron |
Small icosihemidodecahedronIn geometry, the small icosihemidodecahedron is a uniform star polyhedron, indexed as U49. Its vertex figure alternates two regular triangles and decagons as a crossed quadrilateral....
|
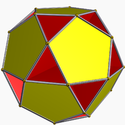Small dodecahemidodecahedronIn geometry, the small dodecahemidodecahedron is a nonconvex uniform polyhedron, indexed as U51. Its vertex figure alternates two regular pentagons and decagons as a crossed quadrilateral....
|
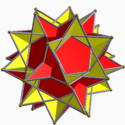Great icosidodecahedron |
Great dodecahemidodecahedronIn geometry, the great dodecahemidodecahedron is a nonconvex uniform polyhedron, indexed as U70. Its vertex figure is a crossed quadrilateral....
|
Great icosihemidodecahedronIn geometry, the great icosihemidodecahedron is a nonconvex uniform polyhedron, indexed as U71. Its vertex figure is a crossed quadrilateral.It is a hemipolyhedron with 6 decagrammic faces passing through the model center.- Related polyhedra :...
|
Dodecadodecahedron |
Small dodecahemicosahedronIn geometry, the small dodecahemicosahedron is a nonconvex uniform polyhedron, indexed as U62. Its vertex figure is a crossed quadrilateral.It is a hemipolyhedron with ten hexagonal faces passing through the model center.- Related polyhedra :...
|
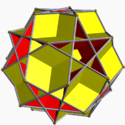Great dodecahemicosahedronIn geometry, the great dodecahemicosahedron is a nonconvex uniform polyhedron, indexed as U65. Its vertex figure is a crossed quadrilateral.It is a hemipolyhedron with ten hexagonal faces passing through the model center.- Related polyhedra :...
|
Compound of five octahedraThis polyhedron can be seen as either a polyhedral stellation or a compound. This compound was first described by Edmund Hess in 1876.- As a stellation :It is the second stellation of the icosahedron, and given as Wenninger model index 23....
|
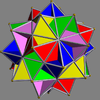Compound of five tetrahemihexahedraA compound of five tetrahemihexahedra is a uniform polyhedron compound and a symmetric arrangement of five tetrahemihexahedra. It is chiral with icosahedral symmetry .- Related polyhedra :...
|
See also
- Cuboctahedron
In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...
- Great truncated icosidodecahedron
- Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
- Rhombicosidodecahedron
In geometry, the rhombicosidodecahedron, or small rhombicosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon faces....
- Truncated icosidodecahedron
In geometry, the truncated icosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces....
External links