Face configuration
Encyclopedia
In geometry, a face configuration is notational description of a face-transitive polyhedron
. It represents a sequential count of the number of faces that exist at each vertex
around a face
.
There is no single standard accepted representation, but one common notation prefixes the description with a V and separates the vertices by a period (.) or a comma (,).
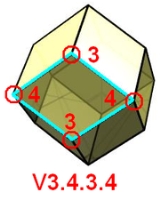
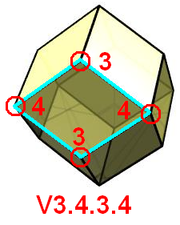 For example, V3.4.3.4 represents the rhombic dodecahedron
For example, V3.4.3.4 represents the rhombic dodecahedron
which is face-transitive: every face is a rhombus
, and alternating vertices of the rhombus contain 3 or 4 faces each.
Another form of this notation, used in Tilings and Patterns, has brackets around the symbol, for instance [3.4.3.4].
Face-transitive polyhedra are generally the polyhedral dual
s of the vertex-transitive
polyhedra, which are described by a parallel vertex configuration
notation. That notation omits the V prefix and represents sequentially the number of edges of the faces around a vertex. For example, 3.4.3.4 is the cuboctahedron
with alternating triangular
and square
faces around each vertex. Polyhedra have the same representation in face configuration notation (with the addition of the V) that their duals have in vertex configuration notation. The rhombic dodecahedron (V3.4.3.4) and the cubocahedron (3.4.3.4) above are dual polyhedra.
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
. It represents a sequential count of the number of faces that exist at each vertex
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
around a face
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
.
There is no single standard accepted representation, but one common notation prefixes the description with a V and separates the vertices by a period (.) or a comma (,).

Rhombic dodecahedron
In geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:...
which is face-transitive: every face is a rhombus
Rhombus
In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...
, and alternating vertices of the rhombus contain 3 or 4 faces each.
Another form of this notation, used in Tilings and Patterns, has brackets around the symbol, for instance [3.4.3.4].
Face-transitive polyhedra are generally the polyhedral dual
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
s of the vertex-transitive
Vertex-transitive
In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same...
polyhedra, which are described by a parallel vertex configuration
Vertex configuration
In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron...
notation. That notation omits the V prefix and represents sequentially the number of edges of the faces around a vertex. For example, 3.4.3.4 is the cuboctahedron
Cuboctahedron
In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...
with alternating triangular
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
and square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
faces around each vertex. Polyhedra have the same representation in face configuration notation (with the addition of the V) that their duals have in vertex configuration notation. The rhombic dodecahedron (V3.4.3.4) and the cubocahedron (3.4.3.4) above are dual polyhedra.
See also
- Platonic solidPlatonic solidIn geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s: five regular polyhedraRegular polyhedronA regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags...
that are either self-dual or whose dual is another Platonic solid. - Catalan solidCatalan solidIn mathematics, a Catalan solid, or Archimedean dual, is a dual polyhedron to an Archimedean solid. The Catalan solids are named for the Belgian mathematician, Eugène Catalan, who first described them in 1865....
s: thirteen polyhedra that are dual to the Archimedean solidArchimedean solidIn geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
s - BipyramidBipyramidAn n-gonal bipyramid or dipyramid is a polyhedron formed by joining an n-gonal pyramid and its mirror image base-to-base.The referenced n-gon in the name of the bipyramids is not an external face but an internal one, existing on the primary symmetry plane which connects the two pyramid halves.The...
s: an infinite set of duals of prismPrism (geometry)In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
s - TrapezohedronTrapezohedronThe n-gonal trapezohedron, antidipyramid or deltohedron is the dual polyhedron of an n-gonal antiprism. Its 2n faces are congruent kites . The faces are symmetrically staggered.The n-gon part of the name does not reference the faces here but arrangement of vertices around an axis of symmetry...
s: an infinite set of duals of antiprismAntiprismIn geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles...
s - List of uniform planar tilings

