
Square tiling
Encyclopedia
In geometry
, the square tiling or square grid is a regular tiling of the Euclidean plane. It has Schläfli symbol of {4,4}, meaning it has 4 squares
around every vertex.
Conway
calls it a quadrille.
The internal angle of the square is 90 degrees so four squares at a point make a full 360 degrees. It is one of three regular tilings of the plane. The other two are the triangular tiling and the hexagonal tiling.
s of a square tiling. (Naming the colors by indices on the 4 squares around a vertex: 1111, 1112(i), 1112(ii), 1122, 1123(i), 1123(ii), 1212, 1213, 1234. (i) cases have simple reflection symmetry, and (ii) glide reflection symmetry.)
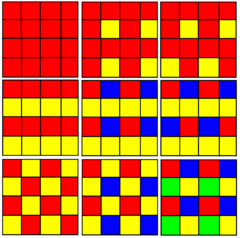
there are eight uniform tilings that can be based from the regular square tiling.
Drawing the tiles colored as red on the original faces, yellow at the original vertices, and blue along the original edges, all 8 forms are distinct. However treating faces identically, there are only three unique topologically forms: square tiling, truncated square tiling
, snub square tiling.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the square tiling or square grid is a regular tiling of the Euclidean plane. It has Schläfli symbol of {4,4}, meaning it has 4 squares
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
around every vertex.
Conway
John Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
calls it a quadrille.
The internal angle of the square is 90 degrees so four squares at a point make a full 360 degrees. It is one of three regular tilings of the plane. The other two are the triangular tiling and the hexagonal tiling.
Uniform colorings
There are 9 distinct uniform coloringUniform coloring
In geometry, a uniform coloring is a property of a uniform figure that is colored to be vertex-transitive...
s of a square tiling. (Naming the colors by indices on the 4 squares around a vertex: 1111, 1112(i), 1112(ii), 1122, 1123(i), 1123(ii), 1212, 1213, 1234. (i) cases have simple reflection symmetry, and (ii) glide reflection symmetry.)

Related polyhedra and tilings
This tiling is topologically related as a part of sequence of regular polyhedra and tilings, extending into the hyperbolic plane: {4,p}, p=3,4,5... {4,3} Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
 {4,4} |
 {4,5} |
 {4,6} |
 {4,7} |
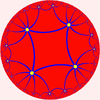 {4,8} |
... |
Wythoff constructions from square tiling
Like the uniform polyhedraUniform polyhedron
A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
there are eight uniform tilings that can be based from the regular square tiling.
Drawing the tiles colored as red on the original faces, yellow at the original vertices, and blue along the original edges, all 8 forms are distinct. However treating faces identically, there are only three unique topologically forms: square tiling, truncated square tiling
Truncated square tiling
In geometry, the truncated square tiling is a semiregular tiling of the Euclidean plane. There is one square and two octagons on each vertex. This is the only edge-to-edge tiling by regular convex polygons which contains an octagon...
, snub square tiling.
| Operation | Schläfli symbol |
Wythoff Symbol Wythoff construction In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :... |
Vertex figure Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron... |
Image |
|---|---|---|---|---|
| Parent | t0{4,4} | 4 | 2 4 | 44 |  |
| Truncation Truncation (geometry) In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :... |
t0,1{4,4} | 2 4 | 4 | 4.8.8 Truncated square tiling In geometry, the truncated square tiling is a semiregular tiling of the Euclidean plane. There is one square and two octagons on each vertex. This is the only edge-to-edge tiling by regular convex polygons which contains an octagon... |
 |
| Rectification Rectification (geometry) In Euclidean geometry, rectification is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points... |
t1{4,4} | 2 | 4 4 | (4.4)2 |  |
| Bitruncation Truncation (geometry) In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :... |
t1,2{4,4} | 2 4 | 4 | 4.8.8 |  |
| Dual Dual polyhedron In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another... |
t2{4,4} | 4 | 2 4 | 44 |  |
| Cantellation Cantellation (geometry) In geometry, a cantellation is an operation in any dimension that cuts a regular polytope at its edges and vertices, creating a new facet in place of each edge and vertex. The operation also applies to regular tilings and honeycombs... |
t0,2{4,4} | 4 4 | 2 | 4.4.4.4 |  |
| Omnitruncation Omnitruncation (geometry) In geometry, an omnitruncation is an operation applied to a regular polytope in a Wythoff construction that creates a maximum number of facets... |
t0,1,2{4,4} | 2 4 4 | | 4.8.8 Truncated square tiling In geometry, the truncated square tiling is a semiregular tiling of the Euclidean plane. There is one square and two octagons on each vertex. This is the only edge-to-edge tiling by regular convex polygons which contains an octagon... |
 |
| Snubbing Snub (geometry) In geometry, an alternation is an operation on a polyhedron or tiling that removes alternate vertices. Only even-sided polyhedra can be alternated, for example the zonohedra. Every 2n-sided face becomes n-sided... |
s{4,4} | | 2 4 4 | 3.3.4.3.4 |  |
See also
- CheckerboardCheckerboardA checkerboard or chequerboard is a board of chequered pattern on which English draughts is played. It is an 8×8 board and the 64 squares are of alternating dark and light color, often red and black....
- List of regular polytopes
- List of uniform tilings
- Square latticeSquare latticeIn mathematics, the square lattice is a type of lattice in a two-dimensional Euclidean space. It is the two-dimensional version of the integer lattice. It is one of the five types of two-dimensional lattices as classified by their symmetry groups; its symmetry group is known symbolically as p4m.Two...
- Tilings of regular polygons

