
Affine geometry
Encyclopedia
In mathematics affine geometry is the study of geometric properties which remain unchanged by affine transformation
s, i.e. non-singular linear transformation
s and translations
. The name affine geometry, like projective geometry
and Euclidean geometry
, follows naturally from the Erlangen program
of Felix Klein
.
Affine geometry is a form of geometry
featuring the unique parallel line property (see the parallel postulate
) where the notion of angle is undefined and lengths cannot be compared in different directions (that is, Euclid's third and fourth postulates are ignored). First identified by Euler, many affine properties are familiar from Euclidean geometry
, but also apply in Minkowski space
. Those properties from Euclidean geometry that are preserved by parallel projection
from one plane
to another are affine. In effect, affine geometry is a generalization of Euclidean geometry characterized by slant and scale distortions. Projective geometry
is more general than affine since it can be derived from projective space by "specializing" any one plane.
In the language of Klein's Erlangen program
, the underlying symmetry
in affine geometry is the group
of affinities, that is, the group of transformations generated by the linear transformation
s of a vector space together with the translation
s by a vector.
Affine geometry can be developed on the basis of linear algebra
. One can define an affine space
as a set of points equipped with a set of transformations, the translations, which forms (the additive group
of) a vector space
(over a given field
), and such that for any given ordered pair of points there is a unique translation sending the first point to the second. In more concrete terms, this amounts to having an operation that associates to any two points a vector, another that allows translation of a point by a vector to give another point, which operations verify a number of axioms (notably two successive translations have the effect of translation by the sum vector). By choosing any point as "origin", the points are in one-to-one correspondence with the vectors, but there is no preferred choice for the origin; thus this approach can be characterized as obtaining the affine space from its associated vector space by "forgetting" the origin (zero vector).
(see chapter XVII). In 1827 August Möbius wrote on affine geometry in his Der barycentrische Calcul, chapter 3.
Only after Felix Klein
's Erlangen program was affine geometry recognized for being a generalization of Euclidean geometry
.
The affine concept of parallelism forms an equivalence relation
on lines. Since the axioms of ordered geometry as presented here include properties that imply the structure of the real numbers, those properties carry over here so that this is an axiomatization of affine geometry over the field of real numbers.
We identify as affine theorems any geometric result that is invariant under the affine group
(in Felix Klein
's Erlangen programme this is its underlying group
of symmetry transformations for affine geometry). Consider in a vector space V, the general linear group
GL(V). It is not the whole affine group because we must allow also translations
by vectors v in V. (Such a translation maps any w in V to w + v.) The affine group is generated by the general linear group and the translations and is in fact their semidirect product
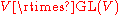 . (Here we think of V as a group under its operation of addition, and use the defining representation of GL(V) on V to define the semidirect product.)
. (Here we think of V as a group under its operation of addition, and use the defining representation of GL(V) on V to define the semidirect product.)
For example, the theorem from the plane geometry of triangles about the concurrence of the lines joining each vertex to the mid-point of the opposite side (at the centroid
or barycenter
) depends on the notions of mid-point and centroid as affine invariants. Other examples include the theorems of Ceva
and Menelaus.
Affine invariants can also assist calculations. For example, the lines that divide the area of a triangle into two equal halves form an envelope
inside the triangle. The ratio of the area of the envelope to the area of the triangle is affine invariant, and so only needs to be calculated from a simple case such as a unit isosceles right angled triangle to give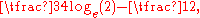 i.e. 0.019860... or less than 2%, for all triangles.
i.e. 0.019860... or less than 2%, for all triangles.
Familiar formulas such as half the base times the height for the area of a triangle, or a third the base times the height for the volume of a pyramid, are likewise affine invariants. While the latter is less obvious than the former for the general case, it is easily seen for the one-sixth of the unit cube formed by a face (area 1) and the midpoint of the cube (height 1/2). Hence it holds for all pyramids, even slanting ones whose apex is not directly above the center of the base, and those with base a parallelogram instead of a square. The formula further generalizes to pyramids whose base can be dissected into parallelograms, including cones by allowing infinitely many parallelograms (with due attention to convergence). The same approach shows that a four-dimensional pyramid has 4D volume one quarter the 3D volume of its parallelopiped base times the height, and so on for higher dimensions.
, of a given dimension n, coordinatized over a field
K. There is also (in two dimensions) a combinatorial generalization of coordinatized affine space, as developed in synthetic finite geometry
. In projective geometry, affine space means the complement of the points (the hyperplane
) at infinity (see also projective space
). Affine space can also be viewed as a vector space whose operations are limited to those linear combinations whose coefficients sum to one, for example 2x−y, x−y+z, (x+y+z)/3, ix+(1-i)y, etc.
Synthetically
, affine planes
are 2-dimensional affine geometries defined in terms of the relations between points and lines (or sometimes, in higher dimensions, hyperplanes). Defining affine (and projective) geometries as configurations of points and lines (or hyperplanes) instead of using coordinates, one gets examples with no coordinate fields. A major property is that all such examples have dimension 2. Finite examples in dimension 2 (finite affine planes) have been valuable in the study of configurations in infinite affine spaces, in group theory
, and in combinatorics
.
Despite being less general than the configurational approach, the other approaches discussed have been very successful in illuminating the parts of geometry that are related to symmetry
.
and projective geometry
. On the one hand, affine geometry is Euclidean geometry with congruence
left out, and on the other hand affine geometry may be obtained from projective geometry by the designation of a particular line or plane to represent the points at infinity. In affine geometry there is no metric
structure but the parallel postulate
does hold. Affine geometry provides the basis for Euclidean structure when perpendicular
lines are defined, or the basis for Minkowski geometry through the notion of hyperbolic orthogonality. In this viewpoint, an affine transformation geometry
is a group of projective transformations that do not permute finite points with points at infinity
Affine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
s, i.e. non-singular linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
s and translations
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
. The name affine geometry, like projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
and Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, follows naturally from the Erlangen program
Erlangen program
An influential research program and manifesto was published in 1872 by Felix Klein, under the title Vergleichende Betrachtungen über neuere geometrische Forschungen...
of Felix Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
.
Affine geometry is a form of geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
featuring the unique parallel line property (see the parallel postulate
Parallel postulate
In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry...
) where the notion of angle is undefined and lengths cannot be compared in different directions (that is, Euclid's third and fourth postulates are ignored). First identified by Euler, many affine properties are familiar from Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, but also apply in Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
. Those properties from Euclidean geometry that are preserved by parallel projection
Parallel projection
Parallel projections have lines of projection that are parallel both in reality and in the projection plane.Parallel projection corresponds to a perspective projection with an infinite focal length , or "zoom".Within parallel projection there is an ancillary category known as "pictorials"...
from one plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
to another are affine. In effect, affine geometry is a generalization of Euclidean geometry characterized by slant and scale distortions. Projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
is more general than affine since it can be derived from projective space by "specializing" any one plane.
In the language of Klein's Erlangen program
Erlangen program
An influential research program and manifesto was published in 1872 by Felix Klein, under the title Vergleichende Betrachtungen über neuere geometrische Forschungen...
, the underlying symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
in affine geometry is the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of affinities, that is, the group of transformations generated by the linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
s of a vector space together with the translation
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
s by a vector.
Affine geometry can be developed on the basis of linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
. One can define an affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
as a set of points equipped with a set of transformations, the translations, which forms (the additive group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of) a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
(over a given field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
), and such that for any given ordered pair of points there is a unique translation sending the first point to the second. In more concrete terms, this amounts to having an operation that associates to any two points a vector, another that allows translation of a point by a vector to give another point, which operations verify a number of axioms (notably two successive translations have the effect of translation by the sum vector). By choosing any point as "origin", the points are in one-to-one correspondence with the vectors, but there is no preferred choice for the origin; thus this approach can be characterized as obtaining the affine space from its associated vector space by "forgetting" the origin (zero vector).
History
In 1748 Euler introduced the term affine (Latin affinis, "related") in his book Introductio in analysin infinitorumIntroductio in analysin infinitorum
Introductio in analysin infinitorum is a two-volume work by Leonhard Euler which lays the foundations of mathematical analysis...
(see chapter XVII). In 1827 August Möbius wrote on affine geometry in his Der barycentrische Calcul, chapter 3.
Only after Felix Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
's Erlangen program was affine geometry recognized for being a generalization of Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
.
Axioms for affine geometry
An axiomatic treatment of plane affine geometry can be built from the axioms of ordered geometry by the addition of two additional axioms.- (Affine axiom of parallelismParallel postulateIn geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry...
) Given a point A and a line r, not through A, there is at most one line through A which does not meet r. - (Desargues) Given seven distinct points A, A', B, B', C, C', O, such that AA', BB', and CC' are distinct lines through O and AB is parallel to A'B' and BC is parallel to B'C', then AC is parallel to A'C'.
The affine concept of parallelism forms an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on lines. Since the axioms of ordered geometry as presented here include properties that imply the structure of the real numbers, those properties carry over here so that this is an axiomatization of affine geometry over the field of real numbers.
Affine transformations
Geometrically, affine transformations (affinities) preserve collinearity. So they transform parallel lines into parallel lines and preserve ratios of distances along parallel lines.We identify as affine theorems any geometric result that is invariant under the affine group
Affine group
In mathematics, the affine group or general affine group of any affine space over a field K is the group of all invertible affine transformations from the space into itself.It is a Lie group if K is the real or complex field or quaternions....
(in Felix Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
's Erlangen programme this is its underlying group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of symmetry transformations for affine geometry). Consider in a vector space V, the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
GL(V). It is not the whole affine group because we must allow also translations
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
by vectors v in V. (Such a translation maps any w in V to w + v.) The affine group is generated by the general linear group and the translations and is in fact their semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
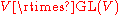 . (Here we think of V as a group under its operation of addition, and use the defining representation of GL(V) on V to define the semidirect product.)
. (Here we think of V as a group under its operation of addition, and use the defining representation of GL(V) on V to define the semidirect product.)For example, the theorem from the plane geometry of triangles about the concurrence of the lines joining each vertex to the mid-point of the opposite side (at the centroid
Centroid
In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...
or barycenter
Barycentric coordinates (astronomy)
In astronomy, barycentric coordinates are non-rotating coordinates with origin at the center of mass of two or more bodies.The barycenter is the point between two objects where they balance each other. For example, it is the center of mass where two or more celestial bodies orbit each other...
) depends on the notions of mid-point and centroid as affine invariants. Other examples include the theorems of Ceva
Ceva's theorem
Ceva's theorem is a theorem about triangles in plane geometry. Given a triangle ABC, let the lines AO, BO and CO be drawn from the vertices to a common point O to meet opposite sides at D, E and F respectively...
and Menelaus.
Affine invariants can also assist calculations. For example, the lines that divide the area of a triangle into two equal halves form an envelope
Envelope (mathematics)
In geometry, an envelope of a family of curves in the plane is a curve that is tangent to each member of the family at some point. Classically, a point on the envelope can be thought of as the intersection of two "adjacent" curves, meaning the limit of intersections of nearby curves...
inside the triangle. The ratio of the area of the envelope to the area of the triangle is affine invariant, and so only needs to be calculated from a simple case such as a unit isosceles right angled triangle to give
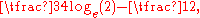 i.e. 0.019860... or less than 2%, for all triangles.
i.e. 0.019860... or less than 2%, for all triangles.Familiar formulas such as half the base times the height for the area of a triangle, or a third the base times the height for the volume of a pyramid, are likewise affine invariants. While the latter is less obvious than the former for the general case, it is easily seen for the one-sixth of the unit cube formed by a face (area 1) and the midpoint of the cube (height 1/2). Hence it holds for all pyramids, even slanting ones whose apex is not directly above the center of the base, and those with base a parallelogram instead of a square. The formula further generalizes to pyramids whose base can be dissected into parallelograms, including cones by allowing infinitely many parallelograms (with due attention to convergence). The same approach shows that a four-dimensional pyramid has 4D volume one quarter the 3D volume of its parallelopiped base times the height, and so on for higher dimensions.
Affine space
Affine geometry can be viewed as the geometry of affine spaceAffine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
, of a given dimension n, coordinatized over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K. There is also (in two dimensions) a combinatorial generalization of coordinatized affine space, as developed in synthetic finite geometry
Finite geometry
A finite geometry is any geometric system that has only a finite number of points.Euclidean geometry, for example, is not finite, because a Euclidean line contains infinitely many points, in fact as many points as there are real numbers...
. In projective geometry, affine space means the complement of the points (the hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
) at infinity (see also projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
). Affine space can also be viewed as a vector space whose operations are limited to those linear combinations whose coefficients sum to one, for example 2x−y, x−y+z, (x+y+z)/3, ix+(1-i)y, etc.
Synthetically
Synthetic geometry
Synthetic or axiomatic geometry is the branch of geometry which makes use of axioms, theorems and logical arguments to draw conclusions, as opposed to analytic and algebraic geometries which use analysis and algebra to perform geometric computations and solve problems.-Logical synthesis:The process...
, affine planes
Affine plane (incidence geometry)
In incidence geometry, an affine plane is a system of points and lines that satisfy the following axioms :* Any two distinct points lie on a unique line.* Given a point and line there is a unique line which contains the point and is parallel to the line...
are 2-dimensional affine geometries defined in terms of the relations between points and lines (or sometimes, in higher dimensions, hyperplanes). Defining affine (and projective) geometries as configurations of points and lines (or hyperplanes) instead of using coordinates, one gets examples with no coordinate fields. A major property is that all such examples have dimension 2. Finite examples in dimension 2 (finite affine planes) have been valuable in the study of configurations in infinite affine spaces, in group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, and in combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
.
Despite being less general than the configurational approach, the other approaches discussed have been very successful in illuminating the parts of geometry that are related to symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
.
Projective view
In traditional geometry, affine geometry is considered to be a study between Euclidean geometryEuclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
and projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
. On the one hand, affine geometry is Euclidean geometry with congruence
Congruence (geometry)
In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
left out, and on the other hand affine geometry may be obtained from projective geometry by the designation of a particular line or plane to represent the points at infinity. In affine geometry there is no metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
structure but the parallel postulate
Parallel postulate
In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry...
does hold. Affine geometry provides the basis for Euclidean structure when perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
lines are defined, or the basis for Minkowski geometry through the notion of hyperbolic orthogonality. In this viewpoint, an affine transformation geometry
Transformation geometry
In mathematics, transformation geometry is a name for a pedagogic theory for teaching Euclidean geometry, based on the Erlangen programme. Felix Klein, who pioneered this point of view, was himself interested in mathematical education. It took many years, though, for his "modern" point of view to...
is a group of projective transformations that do not permute finite points with points at infinity
See also
- Non-Euclidean geometryNon-Euclidean geometryNon-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...
- Affine
- Ordered geometryOrdered geometryOrdered geometry is a form of geometry featuring the concept of intermediacy but, like projective geometry, omitting the basic notion of measurement...
- Euclidean geometryEuclidean geometryEuclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
External links
- Jean H. Gallier (2001) Geometric Methods and Applications for Computer Science and Engineering, Chapter 2:Basics of Affine Geometry, Springer Texts in Applied Mathematics #38, chapter online from University of PennsylvaniaUniversity of PennsylvaniaThe University of Pennsylvania is a private, Ivy League university located in Philadelphia, Pennsylvania, United States. Penn is the fourth-oldest institution of higher education in the United States,Penn is the fourth-oldest using the founding dates claimed by each institution...
(PDF).

