Elliptic geometry
Encyclopedia
Elliptic geometry is a non-Euclidean geometry
, in which, given a line
L and a point
p outside L, there exists no line parallel
to L passing through p. Elliptic geometry, like hyperbolic geometry
, violates Euclid's parallel postulate
, which can be interpreted
as asserting that there is exactly one line parallel to L passing through p. In elliptic geometry, there are no parallel lines at all. Elliptic geometry has a variety of properties that differ from those of classical Euclidean plane geometry. For example, the sum of the angle
s of any triangle
is always greater than 180°.
and thus an imaginative challenge. The elliptic plane is the easiest instance and is based on spherical geometry
. The abstraction involves considering a pair of antipodal points on the sphere to be a single point in the elliptic plane. The breakdown of this identification of two points into one is the premise of H. G. Wells
story "The Remarkable Case of Davidson’s Eyes" (1895). Mathematicians commonly refer to the elliptic plane as the real projective plane
. Especially in spaces of higher dimension, elliptic geometry is called projective geometry
.
As explained by H. S. M. Coxeter
.jpg)
A simple way to picture elliptic geometry is to look at a globe. Neighboring lines of longitude appear to be parallel at the equator, yet they intersect at the poles.
More precisely, the surface of a sphere is a model of elliptic geometry if lines are modeled by great circle
s, and points at each other's antipodes
are considered to be the same point. With this identification of antipodal points, the model satisfies Euclid's first postulate, which states that two points uniquely determine a line. If the antipodal points were considered to be distinct, as in spherical geometry, then uniqueness would be violated, e.g., the lines of longitude on the Earth's surface all pass through both the north pole and the south pole.
Although models such as the spherical model are useful for visualization and for proof of the theory's self-consistency, neither a model nor an embedding in a higher-dimensional space is logically necessary. For example, Einstein's theory of general relativity
has static solutions in which space containing a gravitational field is (locally) described by three-dimensional elliptic geometry, but the theory does not posit the existence of a fourth spatial dimension, or even suggest any way in which the existence of a higher-dimensional space could be detected. (This is unrelated to the treatment of time as a fourth dimension in relativity.) Metaphorically, we can imagine geometers who are like ants living on the surface of a sphere. Even if the ants are unable to move off the surface, they can still construct lines and verify that parallels do not exist. The existence of a third dimension is irrelevant to the ants' ability to do geometry, and its existence is neither verifiable nor necessary from their point of view. Another way of putting this is that the language of the theory's axioms is incapable of expressing the distinction between one model and another.
A great deal of Euclidean geometry carries over directly to elliptic geometry. For example, the first and fourth of Euclid's postulates, that there is a unique line between any two points and that all right angles are equal, hold in elliptic geometry. Postulate 3, that one can construct a circle with any given center and radius, fails if "any radius" is taken to mean "any real number," but holds if it is taken to mean "the length of any given line segment." Therefore any result in Euclidean geometry that follows from these three postulates will hold in elliptic geometry, such as proposition 1 from book I of the Elements, which states that given any line segment, an equilateral triangle can be constructed with the segment as its base.
Elliptic geometry is also like Euclidean geometry in that space is continuous, homogeneous, isotropic, and without boundaries. Isotropy is guaranteed by the fourth postulate, that all right angles are equal. For an example of homogeneity, note that Euclid's proposition I.1 implies that the same equilateral triangle can be constructed at any location, not just in locations that are special in some way. The lack of boundaries follows from the second postulate, extensibility of a line segment.
One way in which elliptic geometry differs from Euclidean geometry is that the sum of the interior angles of a triangle is greater than 180 degrees. In the spherical model, for example, a triangle can be constructed with vertices at the locations where the three positive Cartesian coordinate axes intersect the sphere, and all three of its internal angles are 90 degrees, summing to 270 degrees. For sufficiently small triangles, the excess over 180 degrees can be made as small as desired.
The Pythagorean theorem
fails in elliptic geometry. In the 90-90-90 triangle described above, all three sides have the same length, and they therefore do not satisfy
. The Pythagorean result is recovered in the limit of small triangles.
The ratio of a circle's circumference to its area is smaller than in Euclidean geometry. In general, area and volume do not scale as the second and third powers of linear dimensions.
S3, and these points are well-accessed with the versors in the theory of quaternion
s.
A versor is a quaternion of norm one, which must necessarily have the form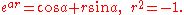
The origin
corresponds to a = 0 and is the identity of the topological group
consisting of versors. With r fixed, the versors
form an elliptic line. The distance from 
to 1 is a . For an arbitrary versor u, the distance will be that θ for which cos θ = (u + u*)/2 since this is the formula for the scalar part of any quaternion.
An elliptic motion is described by the quaternion mapping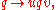
where u and v are fixed versors.
Distances between points are the same as between image points of an elliptic motion. In the case that u and v are quaternion conjugates of one another, the motion is a spatial rotation
, and their vector part is the axis of rotation. In the case u = 1 the elliptic motion is called a right Clifford translation, or a parataxy. The case v = 1 corresponds to left Clifford translation.
Elliptic lines through versor u may be of the form
or 
for a fixed r .
They are the right and left Clifford translations of u along an elliptic line through 1.
The elliptic space is formed by identifying antipodal points on S3.
Elliptic space has special structures called Clifford parallel
s and Clifford surfaces.
s, i.e., intersections of the hypersphere with flat hypersurfaces of dimension n passing through the origin.
are used as points of the model. This models an abstract elliptic geometry that is also known as projective geometry.
The points of n-dimensional projective space can be identified with lines through the origin in (n+1)-dimensional space, and can be represented non-uniquely by nonzero vectors in Rn+1, with the understanding that u and λu, for any non-zero scalar λ, represent the same point. Distance is defined using the metric
that is, the distance between two points is the angle between their corresponding lines in Rn+1. The distance formula is homogeneous in each variable, with d(λu, μv) = d(u, v) if λ and μ are non-zero scalars, so it does define a distance on the points of projective space.
A notable property of the projective elliptic geometry is that for even dimensions, such as the plane, the geometry is nonorientable. It erases the distinction between clockwise and counterclockwise rotation by identifying them.
. Let En represent Rn ∪ {∞}, that is, n-dimensional real space extended by a single point at infinity. We may define a metric, the chordal metric, on
En by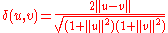
where u and v are any two vectors in Rn and ||*|| is the usual Euclidean norm. We also define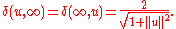
The result is a metric space on En, which represents the distance along a chord of the corresponding points on the hyperspherical model, to which it maps bijectively by stereographic projection. We obtain a model of spherical geometry if we use the metric
Elliptic geometry is obtained from this by identifying the points u and −u/||u||, and taking the distance from v to this pair to be the minimum of the distances from v to each of these two points.
Tarski proved that elementary Euclidean geometry is complete in a certain sense
: there is an algorithm which, for every proposition, can show it to be either true or false. (This does not violate Gödel's theorem
, because Euclidean geometry cannot describe a sufficient amount of arithmetic for the theorem to apply.) It therefore follows that elementary elliptic geometry is also self-consistent and complete.
Non-Euclidean geometry
Non-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...
, in which, given a line
Line (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
L and a point
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
p outside L, there exists no line parallel
Parallel (geometry)
Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...
to L passing through p. Elliptic geometry, like hyperbolic geometry
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
, violates Euclid's parallel postulate
Parallel postulate
In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry...
, which can be interpreted
Playfair's axiom
Playfair's axiom is a geometrical axiom, intended to replace the fifth postulate of Euclides :Given a line and a point not on it, at most one parallel to the given line can be drawn through the point....
as asserting that there is exactly one line parallel to L passing through p. In elliptic geometry, there are no parallel lines at all. Elliptic geometry has a variety of properties that differ from those of classical Euclidean plane geometry. For example, the sum of the angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
s of any triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
is always greater than 180°.
Definition
Elliptic space is an abstract objectAbstract object
An abstract object is an object which does not exist at any particular time or place, but rather exists as a type of thing . In philosophy, an important distinction is whether an object is considered abstract or concrete. Abstract objects are sometimes called abstracta An abstract object is an...
and thus an imaginative challenge. The elliptic plane is the easiest instance and is based on spherical geometry
Spherical geometry
Spherical geometry is the geometry of the two-dimensional surface of a sphere. It is an example of a geometry which is not Euclidean. Two practical applications of the principles of spherical geometry are to navigation and astronomy....
. The abstraction involves considering a pair of antipodal points on the sphere to be a single point in the elliptic plane. The breakdown of this identification of two points into one is the premise of H. G. Wells
H. G. Wells
Herbert George Wells was an English author, now best known for his work in the science fiction genre. He was also a prolific writer in many other genres, including contemporary novels, history, politics and social commentary, even writing text books and rules for war games...
story "The Remarkable Case of Davidson’s Eyes" (1895). Mathematicians commonly refer to the elliptic plane as the real projective plane
Real projective plane
In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
. Especially in spaces of higher dimension, elliptic geometry is called projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
.
As explained by H. S. M. Coxeter
- The name "elliptic" is possibly misleading. It does not imply any direct connection with the curve called an ellipse, but only a rather far-fetched analogy. A central conic is called an ellipse or a hyperbola according as it has no asymptote or two asymptoteAsymptoteIn analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors...
s. Analogously, a non-Euclidean plane is said to be elliptic or hyperbolic according as each of its lineLine (geometry)The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
s contains no point at infinity or two points at infinity.
The spherical model
More precisely, the surface of a sphere is a model of elliptic geometry if lines are modeled by great circle
Great circle
A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...
s, and points at each other's antipodes
Antipodes
In geography, the antipodes of any place on Earth is the point on the Earth's surface which is diametrically opposite to it. Two points that are antipodal to one another are connected by a straight line running through the centre of the Earth....
are considered to be the same point. With this identification of antipodal points, the model satisfies Euclid's first postulate, which states that two points uniquely determine a line. If the antipodal points were considered to be distinct, as in spherical geometry, then uniqueness would be violated, e.g., the lines of longitude on the Earth's surface all pass through both the north pole and the south pole.
Although models such as the spherical model are useful for visualization and for proof of the theory's self-consistency, neither a model nor an embedding in a higher-dimensional space is logically necessary. For example, Einstein's theory of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
has static solutions in which space containing a gravitational field is (locally) described by three-dimensional elliptic geometry, but the theory does not posit the existence of a fourth spatial dimension, or even suggest any way in which the existence of a higher-dimensional space could be detected. (This is unrelated to the treatment of time as a fourth dimension in relativity.) Metaphorically, we can imagine geometers who are like ants living on the surface of a sphere. Even if the ants are unable to move off the surface, they can still construct lines and verify that parallels do not exist. The existence of a third dimension is irrelevant to the ants' ability to do geometry, and its existence is neither verifiable nor necessary from their point of view. Another way of putting this is that the language of the theory's axioms is incapable of expressing the distinction between one model and another.
Comparison with Euclidean geometry
In Euclidean geometry, a figure can be scaled up or scaled down indefinitely, and the resulting figures are similar, i.e., they have the same angles and the same internal proportions. In elliptic geometry this is not the case. For example, in the spherical model we can see that the distance between any two points must be strictly less than half the circumference of the sphere (because antipodal points are identified). A line segment therefore cannot be scaled up indefinitely. A geometer measuring the geometrical properties of the space he or she inhabits can detect, via measurements, that there is a certain distance scale that is a property of the space. On scales much smaller than this one, the space is approximately flat, geometry is approximately Euclidean, and figures can be scaled up and down while remaining approximately similar.A great deal of Euclidean geometry carries over directly to elliptic geometry. For example, the first and fourth of Euclid's postulates, that there is a unique line between any two points and that all right angles are equal, hold in elliptic geometry. Postulate 3, that one can construct a circle with any given center and radius, fails if "any radius" is taken to mean "any real number," but holds if it is taken to mean "the length of any given line segment." Therefore any result in Euclidean geometry that follows from these three postulates will hold in elliptic geometry, such as proposition 1 from book I of the Elements, which states that given any line segment, an equilateral triangle can be constructed with the segment as its base.
Elliptic geometry is also like Euclidean geometry in that space is continuous, homogeneous, isotropic, and without boundaries. Isotropy is guaranteed by the fourth postulate, that all right angles are equal. For an example of homogeneity, note that Euclid's proposition I.1 implies that the same equilateral triangle can be constructed at any location, not just in locations that are special in some way. The lack of boundaries follows from the second postulate, extensibility of a line segment.
One way in which elliptic geometry differs from Euclidean geometry is that the sum of the interior angles of a triangle is greater than 180 degrees. In the spherical model, for example, a triangle can be constructed with vertices at the locations where the three positive Cartesian coordinate axes intersect the sphere, and all three of its internal angles are 90 degrees, summing to 270 degrees. For sufficiently small triangles, the excess over 180 degrees can be made as small as desired.
The Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
fails in elliptic geometry. In the 90-90-90 triangle described above, all three sides have the same length, and they therefore do not satisfy
. The Pythagorean result is recovered in the limit of small triangles.The ratio of a circle's circumference to its area is smaller than in Euclidean geometry. In general, area and volume do not scale as the second and third powers of linear dimensions.
Elliptic space
The three-dimensional elliptic geometry makes use of the 3-sphere3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
S3, and these points are well-accessed with the versors in the theory of quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s.
A versor is a quaternion of norm one, which must necessarily have the form
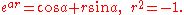
The origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
corresponds to a = 0 and is the identity of the topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
consisting of versors. With r fixed, the versors
form an elliptic line. The distance from to 1 is a . For an arbitrary versor u, the distance will be that θ for which cos θ = (u + u*)/2 since this is the formula for the scalar part of any quaternion.An elliptic motion is described by the quaternion mapping
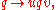where u and v are fixed versors.Distances between points are the same as between image points of an elliptic motion. In the case that u and v are quaternion conjugates of one another, the motion is a spatial rotation
Quaternions and spatial rotation
Unit quaternions provide a convenient mathematical notation for representing orientations and rotations of objects in three dimensions. Compared to Euler angles they are simpler to compose and avoid the problem of gimbal lock. Compared to rotation matrices they are more numerically stable and may...
, and their vector part is the axis of rotation. In the case u = 1 the elliptic motion is called a right Clifford translation, or a parataxy. The case v = 1 corresponds to left Clifford translation.
Elliptic lines through versor u may be of the form
or for a fixed r .They are the right and left Clifford translations of u along an elliptic line through 1.
The elliptic space is formed by identifying antipodal points on S3.
Elliptic space has special structures called Clifford parallel
Clifford parallel
A Clifford parallel is a line which lies at a constant distance from some "base" line but, unlike an ordinary parallel line, does not lie in the same plane...
s and Clifford surfaces.
Hyperspherical model
The hyperspherical model is the generalization of the spherical model to higher dimensions. The points of n-dimensional elliptic space are the pairs of unit vectors (x,−x) in Rn+1, that is, pairs of opposite points on the surface of the unit ball in (n+1)-dimensional space (the n-dimensional hypersphere). Lines in this model are great circleGreat circle
A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...
s, i.e., intersections of the hypersphere with flat hypersurfaces of dimension n passing through the origin.
Projective elliptic geometry
In the projective model of elliptic geometry, the points of n-dimensional real projective spaceReal projective space
In mathematics, real projective space, or RPn, is the topological space of lines through 0 in Rn+1. It is a compact, smooth manifold of dimension n, and a special case of a Grassmannian.-Construction:...
are used as points of the model. This models an abstract elliptic geometry that is also known as projective geometry.
The points of n-dimensional projective space can be identified with lines through the origin in (n+1)-dimensional space, and can be represented non-uniquely by nonzero vectors in Rn+1, with the understanding that u and λu, for any non-zero scalar λ, represent the same point. Distance is defined using the metric
that is, the distance between two points is the angle between their corresponding lines in Rn+1. The distance formula is homogeneous in each variable, with d(λu, μv) = d(u, v) if λ and μ are non-zero scalars, so it does define a distance on the points of projective space.
A notable property of the projective elliptic geometry is that for even dimensions, such as the plane, the geometry is nonorientable. It erases the distinction between clockwise and counterclockwise rotation by identifying them.
Stereographic model
A model representing the same space as the hyperspherical model can be obtained by means of stereographic projectionStereographic projection
The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
. Let En represent Rn ∪ {∞}, that is, n-dimensional real space extended by a single point at infinity. We may define a metric, the chordal metric, on
En by
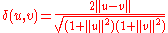
where u and v are any two vectors in Rn and ||*|| is the usual Euclidean norm. We also define
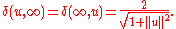
The result is a metric space on En, which represents the distance along a chord of the corresponding points on the hyperspherical model, to which it maps bijectively by stereographic projection. We obtain a model of spherical geometry if we use the metric
Elliptic geometry is obtained from this by identifying the points u and −u/||u||, and taking the distance from v to this pair to be the minimum of the distances from v to each of these two points.
Self-consistency
Because spherical elliptic geometry can be modeled as, for example, a spherical subspace of a Euclidean space, it follows that if Euclidean geometry is self-consistent, so is spherical elliptic geometry. Therefore it is not possible to prove the parallel postulate based on the other four postulates of Euclidean geometry.Tarski proved that elementary Euclidean geometry is complete in a certain sense
Decidability (logic)
In logic, the term decidable refers to the decision problem, the question of the existence of an effective method for determining membership in a set of formulas. Logical systems such as propositional logic are decidable if membership in their set of logically valid formulas can be effectively...
: there is an algorithm which, for every proposition, can show it to be either true or false. (This does not violate Gödel's theorem
Gödel's incompleteness theorems
Gödel's incompleteness theorems are two theorems of mathematical logic that establish inherent limitations of all but the most trivial axiomatic systems capable of doing arithmetic. The theorems, proven by Kurt Gödel in 1931, are important both in mathematical logic and in the philosophy of...
, because Euclidean geometry cannot describe a sufficient amount of arithmetic for the theorem to apply.) It therefore follows that elementary elliptic geometry is also self-consistent and complete.