Grothendieck–Hirzebruch–Riemann–Roch theorem
Encyclopedia
In mathematics
, specifically in algebraic geometry
, the Grothendieck–Riemann–Roch theorem is a far-reaching result on coherent cohomology. It is a generalisation of the Hirzebruch–Riemann–Roch theorem, about complex manifold
s, which is itself a generalisation of the classical Riemann–Roch theorem
for line bundle
s on compact Riemann surface
s.
Riemann–Roch type theorems relate Euler characteristic
s of the cohomology
of a vector bundle
with their topological degrees, or more generally their characteristic classes in (co)homology or algebraic analogues thereof. The classical Riemann–Roch theorem does this for curves and line bundles, whereas the Hirzebruch–Riemann–Roch theorem generalises this to vector bundles over manifolds. The Grothendieck–Hirzebruch–Riemann–Roch theorem sets both theorems in a relative situation of a morphism
between two manifolds (or more general schemes
) and changes the theorem from a statement about a single bundle, to one applying to chain complex
es of sheaves
.
The theorem has been very influential, not least for the development of the Atiyah–Singer index theorem
. Conversely, complex analytic
analogues of the Grothendieck–Hirzebruch–Riemann–Roch theorem can be proved using the families index theorem. Alexander Grothendieck
, its author, was rumored to have finished the proof around 1956 but did not publish his theorem because he was not satisfied with it. Instead Armand Borel
and Jean-Pierre Serre
wrote up and published Grothendieck's preliminary (as he saw it) proof.
quasi-projective scheme over a field
. Under these assumptions, the Grothendieck group
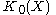
of bounded complexes of coherent sheaves
is canonically isomorphic to the Grothendieck group of bounded complexes of finite-rank vector bundles. Using this isomorphism, consider the Chern character (a rational combination of Chern classes) as a functor
ial transformation
where
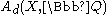
is the Chow group
of cycles on X of dimension d modulo rational equivalence, tensor
ed with the rational number
s. In case X is defined over the complex number
s, the latter group maps to the topological cohomology group
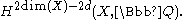
Now consider a proper morphism
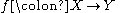
between smooth quasi-projective schemes and a bounded complex of sheaves
The Grothendieck–Riemann–Roch theorem relates the push forward maps
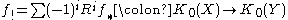
and the pushforward
by the formula
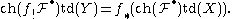
Here td(X) is the Todd genus of (the tangent bundle
of) X. Thus the theorem gives a precise measure for the lack of commutativity of taking the push forwards in the above senses and the Chern character and shows that the needed correction factors depends on X and Y only. In fact, since the Todd genus is functorial and multiplicative in exact sequence
s, we can rewrite the Grothendieck Hirzebruch Riemann Roch formula to
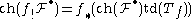
where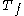
is the relative tangent sheaf of f. This is often useful in applications, for example if f is a locally trivial fibration
.
.
The arithmetic Riemann–Roch theorem extends the Grothendieck–Riemann–Roch theorem to arithmetic schemes.
The Hirzebruch–Riemann–Roch theorem is (essentially) the special case where Y is a point and the field is the field of complex numbers.
's version of the Riemann–Roch theorem was originally conveyed in a letter to Jean-Pierre Serre
around 1956–7. It was made public at the initial Bonn Arbeitstagung, in 1957. Serre and Armand Borel
subsequently organized a seminar at Princeton to understand it. The final published paper was in effect the Borel–Serre exposition.
The significance of Grothendieck's approach rests on several points. First, Grothendieck changed the statement itself: the theorem was, at the time, understood to be a theorem about a variety
, whereas after Grothendieck, it was known to essentially be understood as a theorem about a morphism between varieties. In short, he applied a strong categorical
approach to a hard piece of analysis
. Moreover, Grothendieck introduced K-groups, as discussed above, which paved the way for algebraic K-theory
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, the Grothendieck–Riemann–Roch theorem is a far-reaching result on coherent cohomology. It is a generalisation of the Hirzebruch–Riemann–Roch theorem, about complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
s, which is itself a generalisation of the classical Riemann–Roch theorem
Riemann–Roch theorem
The Riemann–Roch theorem is an important tool in mathematics, specifically in complex analysis and algebraic geometry, for the computation of the dimension of the space of meromorphic functions with prescribed zeroes and allowed poles...
for line bundle
Line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
s on compact Riemann surface
Compact Riemann surface
In mathematics, a compact Riemann surface is a complex manifold of dimension one that is a compact space. Riemann surfaces are generally classified first into the compact and the open .A compact Riemann surface C that is a...
s.
Riemann–Roch type theorems relate Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
s of the cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
of a vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
with their topological degrees, or more generally their characteristic classes in (co)homology or algebraic analogues thereof. The classical Riemann–Roch theorem does this for curves and line bundles, whereas the Hirzebruch–Riemann–Roch theorem generalises this to vector bundles over manifolds. The Grothendieck–Hirzebruch–Riemann–Roch theorem sets both theorems in a relative situation of a morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
between two manifolds (or more general schemes
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
) and changes the theorem from a statement about a single bundle, to one applying to chain complex
Chain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
es of sheaves
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
.
The theorem has been very influential, not least for the development of the Atiyah–Singer index theorem
Atiyah–Singer index theorem
In differential geometry, the Atiyah–Singer index theorem, proved by , states that for an elliptic differential operator on a compact manifold, the analytical index is equal to the topological index...
. Conversely, complex analytic
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
analogues of the Grothendieck–Hirzebruch–Riemann–Roch theorem can be proved using the families index theorem. Alexander Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
, its author, was rumored to have finished the proof around 1956 but did not publish his theorem because he was not satisfied with it. Instead Armand Borel
Armand Borel
Armand Borel was a Swiss mathematician, born in La Chaux-de-Fonds, and was a permanent professor at the Institute for Advanced Study in Princeton, New Jersey, United States from 1957 to 1993...
and Jean-Pierre Serre
Jean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
wrote up and published Grothendieck's preliminary (as he saw it) proof.
Formulation
Let X be a smoothSmooth
Smooth means having a texture that lacks friction. Not rough.Smooth may also refer to:-In mathematics:* Smooth function, a function that is infinitely differentiable; used in calculus and topology...
quasi-projective scheme over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
. Under these assumptions, the Grothendieck group
Grothendieck group
In mathematics, the Grothendieck group construction in abstract algebra constructs an abelian group from a commutative monoid in the best possible way...
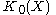
of bounded complexes of coherent sheaves
Coherent sheaf
In mathematics, especially in algebraic geometry and the theory of complex manifolds, coherent sheaves are a specific class of sheaves having particularly manageable properties closely linked to the geometrical properties of the underlying space. The definition of coherent sheaves is made with...
is canonically isomorphic to the Grothendieck group of bounded complexes of finite-rank vector bundles. Using this isomorphism, consider the Chern character (a rational combination of Chern classes) as a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
ial transformation
where
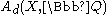
is the Chow group
Chow ring
In algebraic geometry, the Chow ring of an algebraic variety is an algebraic-geometric analogue of the cohomology ring of the variety considered as a topological space: its elements are formed out of actual subvarieties and its multiplicative structure is derived from the intersection of...
of cycles on X of dimension d modulo rational equivalence, tensor
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
ed with the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s. In case X is defined over the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, the latter group maps to the topological cohomology group
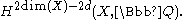
Now consider a proper morphism
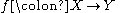
between smooth quasi-projective schemes and a bounded complex of sheaves
The Grothendieck–Riemann–Roch theorem relates the push forward maps
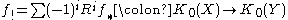
and the pushforward
by the formula
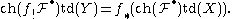
Here td(X) is the Todd genus of (the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
of) X. Thus the theorem gives a precise measure for the lack of commutativity of taking the push forwards in the above senses and the Chern character and shows that the needed correction factors depends on X and Y only. In fact, since the Todd genus is functorial and multiplicative in exact sequence
Exact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
s, we can rewrite the Grothendieck Hirzebruch Riemann Roch formula to
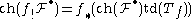
where
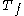is the relative tangent sheaf of f. This is often useful in applications, for example if f is a locally trivial fibrationFibration
In topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
.
Generalising and specialising
Generalisations of the theorem can be made to the non-smooth case by considering an appropriate generalisation of the combination ch(—)td(X) and to the non-proper case by considering cohomology with compact supportCohomology with compact support
In mathematics, cohomology with compact support refers to certain cohomology theories, usually with some condition requiring that cocycles should have compact support.-de Rham cohomology with compact support for smooth manifolds:...
.
The arithmetic Riemann–Roch theorem extends the Grothendieck–Riemann–Roch theorem to arithmetic schemes.
The Hirzebruch–Riemann–Roch theorem is (essentially) the special case where Y is a point and the field is the field of complex numbers.
History
Alexander GrothendieckAlexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
's version of the Riemann–Roch theorem was originally conveyed in a letter to Jean-Pierre Serre
Jean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
around 1956–7. It was made public at the initial Bonn Arbeitstagung, in 1957. Serre and Armand Borel
Armand Borel
Armand Borel was a Swiss mathematician, born in La Chaux-de-Fonds, and was a permanent professor at the Institute for Advanced Study in Princeton, New Jersey, United States from 1957 to 1993...
subsequently organized a seminar at Princeton to understand it. The final published paper was in effect the Borel–Serre exposition.
The significance of Grothendieck's approach rests on several points. First, Grothendieck changed the statement itself: the theorem was, at the time, understood to be a theorem about a variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
, whereas after Grothendieck, it was known to essentially be understood as a theorem about a morphism between varieties. In short, he applied a strong categorical
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
approach to a hard piece of analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
. Moreover, Grothendieck introduced K-groups, as discussed above, which paved the way for algebraic K-theory
Algebraic K-theory
In mathematics, algebraic K-theory is an important part of homological algebra concerned with defining and applying a sequenceof functors from rings to abelian groups, for all integers n....
.