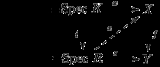
Proper morphism
Encyclopedia
In algebraic geometry
, a proper morphism between schemes
is an analogue of a proper map
between topological space
s.
f : X → Y of algebraic varieties
or schemes
is called universally closed if all its fiber products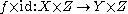
are closed maps of the underlying topological spaces. A morphism
f : X → Y of algebraic varieties
is called proper if it is separated and universally closed. A morphism of schemes is called proper if it is separated, of finite type and universally closed ([EGA] II, 5.4.1 http://modular.fas.harvard.edu/scans/papers/grothendieck/PMIHES_1961__8__5_0.pdf). One also says that X is proper over Y. A variety X over a field
k is complete when the constant morphism from X to a point is proper.
Pd over a field K is proper over a point (that is, Spec(K)). In the more classical language, this is the same as saying that projective space is a complete variety. Projective morphisms are proper, but not all proper morphisms are projective.
Affine varieties of non-zero dimension are never proper. More generally, it can be shown that affine proper morphisms are necessarily finite. For example, it is not hard to see that the affine line A1 is not proper. In fact the map taking A1 to a point x is not universally closed. For example, the morphism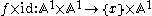
is not closed since the image of the hyperbola uv = 1, which is closed in A1 × A1, is the affine line minus the origin and thus not closed.
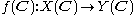
between their sets of complex points with their complex topology (see GAGA
). It can be shown that f is a proper morphism if and only if f(C) is a proper continuous function.
There is a very intuitive criterion for properness which goes back to Chevalley
. It is commonly called the valuative criterion of properness. Let f: X → Y be a morphism of finite type of noetherian schemes. Then f is proper if and only if for all discrete valuation ring
s R with fields of fractions
K and for any K-valued point x ∈ X(K) that maps to a point f(x) that is defined over R, there is a unique lift of x to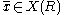
. (EGA II, 7.3.8). Noting that Spec K is the generic point
of Spec R and discrete valuation rings are precisely the regular
local
one-dimensional rings, one may rephrase the criterion: given a regular curve on Y (corresponding to the morphism s : Spec R → Y) and given a lift of the generic point of this curve to X, f is proper if and only if there is exactly one way to complete the curve.
Similarly, f is separated if and only if in all such diagrams, there is at most one lift
.
For example, the projective line
is proper over a field (or even over Z) since one can always scale homogeneous co-ordinates by their least common denominator.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, a proper morphism between schemes
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
is an analogue of a proper map
Proper map
In mathematics, a continuous function between topological spaces is called proper if inverse images of compact subsets are compact. In algebraic geometry, the analogous concept is called a proper morphism.- Definition :...
between topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s.
Definition
A morphismMorphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
f : X → Y of algebraic varieties
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
or schemes
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
is called universally closed if all its fiber products
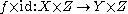
are closed maps of the underlying topological spaces. A morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
f : X → Y of algebraic varieties
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
is called proper if it is separated and universally closed. A morphism of schemes is called proper if it is separated, of finite type and universally closed ([EGA] II, 5.4.1 http://modular.fas.harvard.edu/scans/papers/grothendieck/PMIHES_1961__8__5_0.pdf). One also says that X is proper over Y. A variety X over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
k is complete when the constant morphism from X to a point is proper.
Examples
The projective spaceProjective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
Pd over a field K is proper over a point (that is, Spec(K)). In the more classical language, this is the same as saying that projective space is a complete variety. Projective morphisms are proper, but not all proper morphisms are projective.
Affine varieties of non-zero dimension are never proper. More generally, it can be shown that affine proper morphisms are necessarily finite. For example, it is not hard to see that the affine line A1 is not proper. In fact the map taking A1 to a point x is not universally closed. For example, the morphism
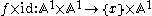
is not closed since the image of the hyperbola uv = 1, which is closed in A1 × A1, is the affine line minus the origin and thus not closed.
Properties and characterizations of proper morphisms
In the following, let f : X → Y be a morphism of varieties or schemes.- If X, Y are varieties over the field of complex numbers C, it induces a continuous function
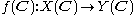
between their sets of complex points with their complex topology (see GAGA
Algebraic geometry and analytic geometry
In mathematics, algebraic geometry and analytic geometry are two closely related subjects. While algebraic geometry studies algebraic varieties, analytic geometry deals with complex manifolds and the more general analytic spaces defined locally by the vanishing of analytic functions of several...
). It can be shown that f is a proper morphism if and only if f(C) is a proper continuous function.
- Properness is a local property on the base, i.e. if Y is covered by some open subschemes Yi and the restriction of f to all f-1(Yi) is proper, then so is f.
- By definition, proper morphisms are stable under base change.
- The compositionFunction compositionIn mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
of two proper morphisms is proper. - Closed immersions are proper.
- More generally, finite morphisms are proper. This is a consequence of the going upGoing up and going downIn commutative algebra, a branch of mathematics, going up and going down are terms which refer to certain properties of chains of prime ideals in integral extensions....
theorem. - Conversely, every quasi-finiteQuasi-finite morphismIn algebraic geometry, a branch of mathematics, a morphism f : X → Y of schemes is quasi-finite if it is finite type and satisfies any of the following equivalent conditions:...
and finite presentation proper morphism is finite. This follows from the so-called Stein factorization, namely the existence of an intermediate scheme such that a morphism can be expressed as one with connected fibres, followed by a finite morphism. (EGA III, 4.3.3) This is a deep theorem. - Proper morphisms are closely related to projective morphisms: If f is proper over a noetherian base Y, then there is a morphism: g: X' →X which is an isomorphism when restricted to a suitable open dense subset: g-1(U) ≅ U, such that f' := fg is projective. This statement is called Chow's lemma.
- Proper finite presentation morphisms of schemes or complex analytic spaces preserve coherent sheaves, in the sense that the higher direct images Rif∗(F) (in particular the direct image f∗(F)) of a coherent sheafCoherent sheafIn mathematics, especially in algebraic geometry and the theory of complex manifolds, coherent sheaves are a specific class of sheaves having particularly manageable properties closely linked to the geometrical properties of the underlying space. The definition of coherent sheaves is made with...
F are coherent (EGA III, 3.2.1). This boils down to the fact that the cohomology groups of projective spaceProjective spaceIn mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
over some fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
k with respect to coherent sheaves are finitely generated over k, a statement which fails for non-projective varieties: consider C∗, the punctured disc and its sheaf of holomorphic functionHolomorphic functionIn mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s
. Its sections 
is the ring of Laurent polynomials, which is infinitely generated over C. - If f: X→Y and g:Y→Z are such that gf is proper and g is separated, then f is proper. This can for example be easily proven using the following criterion:
Valuative criterion of properness
Claude Chevalley
Claude Chevalley was a French mathematician who made important contributions to number theory, algebraic geometry, class field theory, finite group theory, and the theory of algebraic groups...
. It is commonly called the valuative criterion of properness. Let f: X → Y be a morphism of finite type of noetherian schemes. Then f is proper if and only if for all discrete valuation ring
Discrete valuation ring
In abstract algebra, a discrete valuation ring is a principal ideal domain with exactly one non-zero maximal ideal.This means a DVR is an integral domain R which satisfies any one of the following equivalent conditions:...
s R with fields of fractions
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
K and for any K-valued point x ∈ X(K) that maps to a point f(x) that is defined over R, there is a unique lift of x to
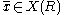. (EGA II, 7.3.8). Noting that Spec K is the generic pointGeneric point
In mathematics, in the fields general topology and particularly of algebraic geometry, a generic point P of a topological space X is an algebraic way of capturing the notion of a generic property: a generic property is a property of the generic point.- Definition and motivation :A generic point of...
of Spec R and discrete valuation rings are precisely the regular
Regular ring
In commutative algebra, a regular ring is a commutative noetherian ring, such that the localization at every prime ideal is a regular local ring: that is, every such localization has the property that the minimal number of generators of its maximal ideal is equal to its Krull dimension.Jean-Pierre...
local
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
one-dimensional rings, one may rephrase the criterion: given a regular curve on Y (corresponding to the morphism s : Spec R → Y) and given a lift of the generic point of this curve to X, f is proper if and only if there is exactly one way to complete the curve.
Similarly, f is separated if and only if in all such diagrams, there is at most one lift
.For example, the projective line
Projective line
In mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see...
is proper over a field (or even over Z) since one can always scale homogeneous co-ordinates by their least common denominator.