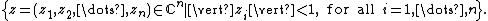Complex manifold
Encyclopedia
In differential geometry, a complex manifold is a manifold
with an atlas
of charts to the open unit disk in Cn, such that the transition map
s are holomorphic.
The term complex manifold is variously used to mean a complex manifold in the sense above (which can be specified as an integrable complex manifold), and an almost-complex manifold, as discussed below.
s are much more rigid than smooth function
s, the theories of smooth and complex manifolds have very different flavors: compact complex manifolds are much closer to algebraic varieties
than to differentiable manifolds.
For example, the Whitney embedding theorem tells us that every smooth manifold can be embedded as a smooth submanifold of Rn, whereas it is "rare" for a complex manifold to have a holomorphic embedding into Cn. Consider for example any compact
connected complex manifold M: any holomorphic function on it is locally constant by Liouville's theorem
. Now if we had a holomorphic embedding of M into Cn, then the coordinate functions of Cn would restrict to nonconstant holomorphic functions on M, contradicting compactness, except in the case that M is just a point. Complex manifolds that can be embedded in Cn are called Stein manifold
s and form a very special class of manifolds including, for example, smooth complex affine algebraic varieties.
The classification of complex manifolds is much more subtle than that of differentiable manifolds. For example, while in dimensions other than four, a given topological manifold has at most finitely many smooth structure
s, a topological manifold supporting a complex structure can and often does support uncountably many complex structures. Riemann surface
s, two dimensional manifolds equipped with a complex structure, which are topologically classified by the genus
, are an important example of this phenomenon. The set of complex structures on a given orientable surface, modulo biholomorphic equivalence, itself forms a complex algebraic variety called a moduli space
, the structure of which remains an area of active research.
Since the transition maps between charts are biholomorphic, complex manifolds are, in particular, smooth and canonically oriented (not just orientable: a biholomorphic map to (a subset of) Cn gives an orientation, as biholomorphic maps are orientation-preserving).
Similarly, the quaternionic analogs of these are also complex manifolds.
Note that there are inclusions between these as
Δ ⊆ C ⊆ Ĉ, but that there are no non-constant maps in the other direction, by
Liouville's theorem
.
s) – that is, the tangent bundle is equipped with a linear complex structure
.
Concretely, this is an endomorphism
of the tangent bundle
whose square is −I; this endomorphism is analogous to multiplication by the imaginary number i, and is denoted J (to avoid confusion with the identity matrix I). An almost complex manifold is necessarily even dimensional.
An almost complex structure is weaker than a complex structure: any complex manifold has an almost complex structure, but not every almost complex structure comes from a complex structure. Note that every even dimensional real manifold has an almost complex structure defined locally from the local coordinate chart. The question is whether this complex structure can be defined globally. An almost complex structure that comes from a complex structure is called integrable, and when one wishes to specify a complex structure as opposed to an almost complex structure, one says an integrable complex structure. For integrable complex structures the so-called Nijenhuis tensor vanishes. This tensor is defined on pairs of vector fields, X, Y by
For example, the 6-dimensional sphere
S6 has a natural almost complex structure arising from the fact that it is the orthogonal complement of i in the unit sphere of the octonion
s, but this is not a complex structure. (It is not currently known whether or not the 6-sphere has a complex structure.) Using an almost complex structure we can make sense of holomorphic maps and ask about the existence of holomorphic coordinates on the manifold. The existence of holomorphic coordinates is equivalent to saying the manifold is complex (which is what the chart definition says).
Tensoring the tangent bundle with the complex numbers we get the complexified tangent bundle, on which multiplication by complex numbers makes sense (even if we started with a real manifold). The eigenvalues of an almost complex structure are ±i and the eigenspaces form sub-bundles denoted by T 0, 1M and T 1, 0M. The Newlander–Niremberg theorem shows that an almost complex structure is actually a complex structure precisely when these subbundles are involutive, i.e., closed under the Lie bracket of vector fields, and such an almost complex structure is called integrable.
Examples of Kähler manifolds include smooth projective varieties and more generally any complex submanifold of a Kähler manifold. The Hopf manifolds are examples of complex manifolds that are not Kähler. To construct one, take a complex vector space minus the origin and consider the action of the group of integers on this space by multiplication by exp(n). The quotient is a complex manifold whose first Betti number
is one, so by the Hodge theorem, it cannot be Kähler.
A Calabi–Yau manifold is a compact Ricci-flat Kähler manifold or equivalently one whose first Chern class
vanishes.
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
with an atlas
Atlas (topology)
In mathematics, particularly topology, one describesa manifold using an atlas. An atlas consists of individualcharts that, roughly speaking, describe individual regionsof the manifold. If the manifold is the surface of the Earth,...
of charts to the open unit disk in Cn, such that the transition map
Atlas (topology)
In mathematics, particularly topology, one describesa manifold using an atlas. An atlas consists of individualcharts that, roughly speaking, describe individual regionsof the manifold. If the manifold is the surface of the Earth,...
s are holomorphic.
The term complex manifold is variously used to mean a complex manifold in the sense above (which can be specified as an integrable complex manifold), and an almost-complex manifold, as discussed below.
Implications of complex structure
Since holomorphic functionHolomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s are much more rigid than smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s, the theories of smooth and complex manifolds have very different flavors: compact complex manifolds are much closer to algebraic varieties
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
than to differentiable manifolds.
For example, the Whitney embedding theorem tells us that every smooth manifold can be embedded as a smooth submanifold of Rn, whereas it is "rare" for a complex manifold to have a holomorphic embedding into Cn. Consider for example any compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
connected complex manifold M: any holomorphic function on it is locally constant by Liouville's theorem
Liouville's theorem (complex analysis)
In complex analysis, Liouville's theorem, named after Joseph Liouville, states that every bounded entire function must be constant. That is, every holomorphic function f for which there exists a positive number M such that |f| ≤ M for all z in C is constant.The theorem is considerably improved by...
. Now if we had a holomorphic embedding of M into Cn, then the coordinate functions of Cn would restrict to nonconstant holomorphic functions on M, contradicting compactness, except in the case that M is just a point. Complex manifolds that can be embedded in Cn are called Stein manifold
Stein manifold
In mathematics, a Stein manifold in the theory of several complex variables and complex manifolds is a complex submanifold of the vector space of n complex dimensions. The name is for Karl Stein.- Definition :...
s and form a very special class of manifolds including, for example, smooth complex affine algebraic varieties.
The classification of complex manifolds is much more subtle than that of differentiable manifolds. For example, while in dimensions other than four, a given topological manifold has at most finitely many smooth structure
Smooth structure
In mathematics, a smooth structure on a manifold allows for an unambiguous notion of smooth function. In particular, a smooth structure allows one to perform mathematical analysis on the manifold....
s, a topological manifold supporting a complex structure can and often does support uncountably many complex structures. Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
s, two dimensional manifolds equipped with a complex structure, which are topologically classified by the genus
Genus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
, are an important example of this phenomenon. The set of complex structures on a given orientable surface, modulo biholomorphic equivalence, itself forms a complex algebraic variety called a moduli space
Moduli space
In algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
, the structure of which remains an area of active research.
Since the transition maps between charts are biholomorphic, complex manifolds are, in particular, smooth and canonically oriented (not just orientable: a biholomorphic map to (a subset of) Cn gives an orientation, as biholomorphic maps are orientation-preserving).
Examples of complex manifolds
- Riemann surfaceRiemann surfaceIn mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
s. - The Cartesian product of two complex manifolds.
- The inverse image of any noncritical value of a holomorphic map.
Smooth complex algebraic varieties
Smooth complex algebraic varieties are complex manifolds, including:- Complex vector spaces.
- Complex projective spaceComplex projective spaceIn mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines...
s, CPn. - Complex GrassmannianGrassmannianIn mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...
s. - Complex Lie groups such as GL(n, C) or Sp(n, C).
Similarly, the quaternionic analogs of these are also complex manifolds.
Simply connected
The simply connected 1-dimensional complex manifolds are isomorphic to either:- Δ, the unit disk in C
- C, the complex plane
- Ĉ, the Riemann sphereRiemann sphereIn mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
Note that there are inclusions between these as
Δ ⊆ C ⊆ Ĉ, but that there are no non-constant maps in the other direction, by
Liouville's theorem
Liouville's theorem (complex analysis)
In complex analysis, Liouville's theorem, named after Joseph Liouville, states that every bounded entire function must be constant. That is, every holomorphic function f for which there exists a positive number M such that |f| ≤ M for all z in C is constant.The theorem is considerably improved by...
.
Disk vs. space vs. polydisk
The following spaces are different as complex manifolds, demonstrating the more rigid geometric character of complex manifolds (compared to smooth manifolds):- the unit disk or open ball, {z ∈ Cn : ||z|| < 1}
- complex space Cn
- the polydisk
Almost complex structures
An almost complex structure on a real manifold is a GLn(C)-structure (in the sense of G-structureG-structure
In differential geometry, a G-structure on an n-manifold M, for a given structure group G, is a G-subbundle of the tangent frame bundle FM of M....
s) – that is, the tangent bundle is equipped with a linear complex structure
Linear complex structure
In mathematics, a complex structure on a real vector space V is an automorphism of V that squares to the minus identity, −I. Such a structure on V allows one to define multiplication by complex scalars in a canonical fashion so as to regard V as a complex vector space.Complex structures have...
.
Concretely, this is an endomorphism
Endomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
of the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
whose square is −I; this endomorphism is analogous to multiplication by the imaginary number i, and is denoted J (to avoid confusion with the identity matrix I). An almost complex manifold is necessarily even dimensional.
An almost complex structure is weaker than a complex structure: any complex manifold has an almost complex structure, but not every almost complex structure comes from a complex structure. Note that every even dimensional real manifold has an almost complex structure defined locally from the local coordinate chart. The question is whether this complex structure can be defined globally. An almost complex structure that comes from a complex structure is called integrable, and when one wishes to specify a complex structure as opposed to an almost complex structure, one says an integrable complex structure. For integrable complex structures the so-called Nijenhuis tensor vanishes. This tensor is defined on pairs of vector fields, X, Y by
- NJ(X, Y) = [X, Y] + J[JX, Y] + J[X, JY] − [JX, JY].
For example, the 6-dimensional sphere
Hypersphere
In mathematics, an n-sphere is a generalization of the surface of an ordinary sphere to arbitrary dimension. For any natural number n, an n-sphere of radius r is defined as the set of points in -dimensional Euclidean space which are at distance r from a central point, where the radius r may be any...
S6 has a natural almost complex structure arising from the fact that it is the orthogonal complement of i in the unit sphere of the octonion
Octonion
In mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
s, but this is not a complex structure. (It is not currently known whether or not the 6-sphere has a complex structure.) Using an almost complex structure we can make sense of holomorphic maps and ask about the existence of holomorphic coordinates on the manifold. The existence of holomorphic coordinates is equivalent to saying the manifold is complex (which is what the chart definition says).
Tensoring the tangent bundle with the complex numbers we get the complexified tangent bundle, on which multiplication by complex numbers makes sense (even if we started with a real manifold). The eigenvalues of an almost complex structure are ±i and the eigenspaces form sub-bundles denoted by T 0, 1M and T 1, 0M. The Newlander–Niremberg theorem shows that an almost complex structure is actually a complex structure precisely when these subbundles are involutive, i.e., closed under the Lie bracket of vector fields, and such an almost complex structure is called integrable.
Kähler and Calabi–Yau manifolds
One can define an analogue of a Riemannian metric for complex manifolds, called a Hermitian metric. Like a Riemannian metric, a Hermitian metric consists of a smoothly varying, positive definite inner product on the tangent bundle, which is Hermitian with respect to the complex structure on the tangent space at each point. As in the Riemannian case, such metrics always exist in abundance on any complex manifold. If the skew symmetric part of such a metric is symplectic, i.e. closed and nondegenerate, then the metric is called Kähler. Kähler structures are much more difficult to come by and are much more rigid.Examples of Kähler manifolds include smooth projective varieties and more generally any complex submanifold of a Kähler manifold. The Hopf manifolds are examples of complex manifolds that are not Kähler. To construct one, take a complex vector space minus the origin and consider the action of the group of integers on this space by multiplication by exp(n). The quotient is a complex manifold whose first Betti number
Betti number
In algebraic topology, a mathematical discipline, the Betti numbers can be used to distinguish topological spaces. Intuitively, the first Betti number of a space counts the maximum number of cuts that can be made without dividing the space into two pieces....
is one, so by the Hodge theorem, it cannot be Kähler.
A Calabi–Yau manifold is a compact Ricci-flat Kähler manifold or equivalently one whose first Chern class
Chern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
vanishes.