Gravitational singularity
Encyclopedia
A gravitational singularity or spacetime singularity is a location where the quantities that are used to measure the gravitational field become infinite
in a way that does not depend on the coordinate system. These quantities are the scalar invariant curvature
s of spacetime, which includes a measure of the density of matter.
For the purposes of proving the Penrose–Hawking singularity theorems, a spacetime
with a singularity is defined to be one that contains geodesics
that cannot be extended in a smooth
manner. The end of such a geodesic is considered to be the singularity. This is a different definition, useful for proving theorems.
The two most important types of spacetime singularities are curvature singularities and conical singularities. Singularities can also be divided according to whether they are covered by an event horizon
or not (naked singularities
). According to a naive interpretation of general relativity
that ignores quantum mechanics
, the initial state of the universe
, at the beginning of the Big Bang
, was a singularity. Both General Relativity and Quantum Mechanics break down in describing the Big Bang, but in general quantum mechanics does not permit particles to inhabit a space smaller than their wavelengths. Another type of singularity predicted by general relativity is inside a black hole
: any star
collapsing beyond a certain point (the Schwarzschild radius
) would form a black hole, inside which a singularity (covered by an event horizon) would be formed, as all the matter would flow into a certain point (or a circular line, if the black hole is rotating). This is again according to General Relativity without Quantum Mechanics, which forbids wavelike particles entering a space smaller than their wavelength. These hypothetical singularities are also known as curvature singularities.
of some quantity becomes infinite or increases without limit. This is generally a sign for a missing piece in the theory, as in the Ultraviolet Catastrophe
, renormalization
, and instability of a hydrogen atom predicted by the Larmor Formula
.
In supersymmetry
, a singularity in the moduli space
happens usually when there are additional mass
less degrees of freedom in that certain point. Similarly, it is thought that singularities in spacetime often mean that there are additional degrees of freedom
that exist only within the vicinity of the singularity. The same fields related to the whole spacetime, also exist; for example, the electromagnetic field
. In known examples of string theory
, the latter degrees of freedom are related to closed strings, while the degrees of freedom are "stuck" to the singularity and related either to open strings or to the twisted sector of an orbifold
.
Some theories, such as the theory of Loop quantum gravity
suggest that singularities may not exist. The idea is that due to quantum gravity
effects, there is a minimum distance beyond which the force of gravity no longer continues to increase as the distance between the masses become shorter.
or another theory of gravity (such as supergravity
), often result in encountering points where the metric
blows up to infinity. However, many of these points are in fact completely regular
. Moreover, the infinities are merely a result of using an inappropriate coordinate system
at this point. Thus, in order to test whether there is a singularity at a certain point, one must check whether at this point diffeomorphism invariant quantities (i.e. scalar
s) become infinite. Such quantities are the same in every coordinate system, so these infinities will not "go away" by a change of coordinates.
An example is the Schwarzschild
solution that describes a non-rotating, uncharged
black hole. In coordinate systems convenient for working in regions far away from the black hole, a part of the metric becomes infinite at the event horizon
. However, spacetime
at the event horizon is regular
. The regularity becomes evident when changing to another coordinate system (such as the Kruskal coordinates), where the metric is perfectly smooth
. On the other hand, in the center of the black hole
, where the metric becomes infinite as well, the solutions suggest singularity exists. The existence of the singularity can be verified by noting that the Kretschmann scalar
or square of the Riemann tensor,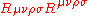
, which is diffeomorphism invariant, is infinite.
While in a non-rotating black hole the singularity occurs at a single point in the model coordinates, called a "point singularity". In a rotating black hole, also known as a Kerr black hole, the singularity occurs on a ring (a circular line), defined as a "ring singularity
". Such a singularity may also theoretically become a wormhole
.
More generally, a spacetime is considered singular if it is geodesically incomplete, meaning that there are freely-falling particles whose motion cannot be determined at a finite time at the point of reaching the singularity. For example, any observer below the event horizon
of a non-rotating black hole would fall into its center within a finite period of time. The classical version of the Big Bang
cosmological
model of the universe
contains a causal singularity at the start of time
(t=0), where all time-like geodesics have no extensions into the past. Extrapolating backward to this hypothetical time 0 results in a universe of size 0 in all spatial dimensions, infinite density, infinite temperature, and infinite space-time curvature.
is not smooth at the point of the limit itself. Thus, spacetime looks like a cone
around this point, where the singularity is located at the tip of the cone. The metric can be finite everywhere if a suitable coordinate system
is used.
An example of such a conical singularity is a cosmic string
.
hides every singularity behind an event horizon, making naked singularities impossible. This is referred to as the cosmic censorship hypothesis
. However, in 1991, physicians Stuart Shapiro and Saul Teukolsky
performed computer simulations of a rotating plane of dust that indicated that general relativity might allow for "naked" singularities. What these objects would actually look like in such a model is unknown. Nor is it known whether singularities would still arise if the simplifying assumptions used to make the simulation were removed.
came up with the concept of Hawking radiation, the question of black holes having entropy was avoided. However, this concept demonstrates that black holes can radiate energy, which conserves entropy and solves the incompatibility problems with the second law of thermodynamics. Entropy, however, implies heat and therefore temperature. The loss of energy also suggests that black holes do not last forever, but rather "evaporate" slowly. Small black holes tend to be hotter whereas larger ones tend to be colder. All known black hole candidates are so large that their temperature is far below that of the cosmic background radiation, so they are all gaining energy. They will not begin to lose energy until a cosmological redshift of more than one million is reached, rather than the thousand or so since the background radiation formed.
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
in a way that does not depend on the coordinate system. These quantities are the scalar invariant curvature
Curvature of Riemannian manifolds
In mathematics, specifically differential geometry, the infinitesimal geometry of Riemannian manifolds with dimension at least 3 is too complicated to be described by a single number at a given point. Riemann introduced an abstract and rigorous way to define it, now known as the curvature tensor...
s of spacetime, which includes a measure of the density of matter.
For the purposes of proving the Penrose–Hawking singularity theorems, a spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
with a singularity is defined to be one that contains geodesics
Geodesic (general relativity)
In general relativity, a geodesic generalizes the notion of a "straight line" to curved spacetime. Importantly, the world line of a particle free from all external, non-gravitational, force is a particular type of geodesic...
that cannot be extended in a smooth
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
manner. The end of such a geodesic is considered to be the singularity. This is a different definition, useful for proving theorems.
The two most important types of spacetime singularities are curvature singularities and conical singularities. Singularities can also be divided according to whether they are covered by an event horizon
Event horizon
In general relativity, an event horizon is a boundary in spacetime beyond which events cannot affect an outside observer. In layman's terms it is defined as "the point of no return" i.e. the point at which the gravitational pull becomes so great as to make escape impossible. The most common case...
or not (naked singularities
Naked singularity
In general relativity, a naked singularity is a gravitational singularity, without an event horizon. In a black hole, there is a region around the singularity, the event horizon, where the gravitational force of the singularity is strong enough so that light cannot escape. Hence, the singularity...
). According to a naive interpretation of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
that ignores quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, the initial state of the universe
Universe
The Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...
, at the beginning of the Big Bang
Big Bang
The Big Bang theory is the prevailing cosmological model that explains the early development of the Universe. According to the Big Bang theory, the Universe was once in an extremely hot and dense state which expanded rapidly. This rapid expansion caused the young Universe to cool and resulted in...
, was a singularity. Both General Relativity and Quantum Mechanics break down in describing the Big Bang, but in general quantum mechanics does not permit particles to inhabit a space smaller than their wavelengths. Another type of singularity predicted by general relativity is inside a black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
: any star
Star
A star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
collapsing beyond a certain point (the Schwarzschild radius
Schwarzschild radius
The Schwarzschild radius is the distance from the center of an object such that, if all the mass of the object were compressed within that sphere, the escape speed from the surface would equal the speed of light...
) would form a black hole, inside which a singularity (covered by an event horizon) would be formed, as all the matter would flow into a certain point (or a circular line, if the black hole is rotating). This is again according to General Relativity without Quantum Mechanics, which forbids wavelike particles entering a space smaller than their wavelength. These hypothetical singularities are also known as curvature singularities.
Interpretation
Many theories in physics have mathematical singularities of one kind or another. Equations for these physical theories predict that the rate of changeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of some quantity becomes infinite or increases without limit. This is generally a sign for a missing piece in the theory, as in the Ultraviolet Catastrophe
Ultraviolet catastrophe
The ultraviolet catastrophe, also called the Rayleigh–Jeans catastrophe, was a prediction of late 19th century/early 20th century classical physics that an ideal black body at thermal equilibrium will emit radiation with infinite power....
, renormalization
Renormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
, and instability of a hydrogen atom predicted by the Larmor Formula
Larmor formula
In physics, in the area of electrodynamics, the Larmor formula is used to calculate the total power radiated by a nonrelativistic point charge as it accelerates. It was first derived by J. J...
.
In supersymmetry
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
, a singularity in the moduli space
Moduli space
In algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
happens usually when there are additional mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
less degrees of freedom in that certain point. Similarly, it is thought that singularities in spacetime often mean that there are additional degrees of freedom
Degrees of freedom (physics and chemistry)
A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...
that exist only within the vicinity of the singularity. The same fields related to the whole spacetime, also exist; for example, the electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
. In known examples of string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
, the latter degrees of freedom are related to closed strings, while the degrees of freedom are "stuck" to the singularity and related either to open strings or to the twisted sector of an orbifold
Orbifold
In the mathematical disciplines of topology, geometry, and geometric group theory, an orbifold is a generalization of a manifold...
.
Some theories, such as the theory of Loop quantum gravity
Loop quantum gravity
Loop quantum gravity , also known as loop gravity and quantum geometry, is a proposed quantum theory of spacetime which attempts to reconcile the theories of quantum mechanics and general relativity...
suggest that singularities may not exist. The idea is that due to quantum gravity
Quantum gravity
Quantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
effects, there is a minimum distance beyond which the force of gravity no longer continues to increase as the distance between the masses become shorter.
Curvature
Solutions to the equations of general relativityGeneral relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
or another theory of gravity (such as supergravity
Supergravity
In theoretical physics, supergravity is a field theory that combines the principles of supersymmetry and general relativity. Together, these imply that, in supergravity, the supersymmetry is a local symmetry...
), often result in encountering points where the metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
blows up to infinity. However, many of these points are in fact completely regular
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
. Moreover, the infinities are merely a result of using an inappropriate coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
at this point. Thus, in order to test whether there is a singularity at a certain point, one must check whether at this point diffeomorphism invariant quantities (i.e. scalar
Scalar (physics)
In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...
s) become infinite. Such quantities are the same in every coordinate system, so these infinities will not "go away" by a change of coordinates.
An example is the Schwarzschild
Schwarzschild metric
In Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...
solution that describes a non-rotating, uncharged
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
black hole. In coordinate systems convenient for working in regions far away from the black hole, a part of the metric becomes infinite at the event horizon
Event horizon
In general relativity, an event horizon is a boundary in spacetime beyond which events cannot affect an outside observer. In layman's terms it is defined as "the point of no return" i.e. the point at which the gravitational pull becomes so great as to make escape impossible. The most common case...
. However, spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
at the event horizon is regular
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
. The regularity becomes evident when changing to another coordinate system (such as the Kruskal coordinates), where the metric is perfectly smooth
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
. On the other hand, in the center of the black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
, where the metric becomes infinite as well, the solutions suggest singularity exists. The existence of the singularity can be verified by noting that the Kretschmann scalar
Kretschmann scalar
In the theory of Lorentzian manifolds, particularly in the context of applications to general relativity, the Kretschmann scalar is a quadratic scalar invariant. It was introduced by Erich Kretschmann.-Definition:...
or square of the Riemann tensor,
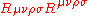, which is diffeomorphism invariant, is infinite.While in a non-rotating black hole the singularity occurs at a single point in the model coordinates, called a "point singularity". In a rotating black hole, also known as a Kerr black hole, the singularity occurs on a ring (a circular line), defined as a "ring singularity
Ring singularity
Ring singularity is a term used in general relativity to describe the altering gravitational singularity of a rotating black hole, or a Kerr black hole, so that the gravitational singularity becomes shaped like a ring.-Description of a ring-singularity:...
". Such a singularity may also theoretically become a wormhole
Wormhole
In physics, a wormhole is a hypothetical topological feature of spacetime that would be, fundamentally, a "shortcut" through spacetime. For a simple visual explanation of a wormhole, consider spacetime visualized as a two-dimensional surface. If this surface is folded along a third dimension, it...
.
More generally, a spacetime is considered singular if it is geodesically incomplete, meaning that there are freely-falling particles whose motion cannot be determined at a finite time at the point of reaching the singularity. For example, any observer below the event horizon
Event horizon
In general relativity, an event horizon is a boundary in spacetime beyond which events cannot affect an outside observer. In layman's terms it is defined as "the point of no return" i.e. the point at which the gravitational pull becomes so great as to make escape impossible. The most common case...
of a non-rotating black hole would fall into its center within a finite period of time. The classical version of the Big Bang
Big Bang
The Big Bang theory is the prevailing cosmological model that explains the early development of the Universe. According to the Big Bang theory, the Universe was once in an extremely hot and dense state which expanded rapidly. This rapid expansion caused the young Universe to cool and resulted in...
cosmological
Physical cosmology
Physical cosmology, as a branch of astronomy, is the study of the largest-scale structures and dynamics of the universe and is concerned with fundamental questions about its formation and evolution. For most of human history, it was a branch of metaphysics and religion...
model of the universe
Universe
The Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...
contains a causal singularity at the start of time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
(t=0), where all time-like geodesics have no extensions into the past. Extrapolating backward to this hypothetical time 0 results in a universe of size 0 in all spatial dimensions, infinite density, infinite temperature, and infinite space-time curvature.
Conical
A conical singularity occurs when there is a point where the limit of every diffeomorphism invariant quantity is finite. In which case, spacetimeSpacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
is not smooth at the point of the limit itself. Thus, spacetime looks like a cone
Cone (geometry)
A cone is an n-dimensional geometric shape that tapers smoothly from a base to a point called the apex or vertex. Formally, it is the solid figure formed by the locus of all straight line segments that join the apex to the base...
around this point, where the singularity is located at the tip of the cone. The metric can be finite everywhere if a suitable coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
is used.
An example of such a conical singularity is a cosmic string
Cosmic string
Cosmic strings are hypothetical 1-dimensional topological defects which may have formed during a symmetry breaking phase transition in the early universe when the topology of the vacuum manifold associated to this symmetry breaking is not simply connected. It is expected that at least one string...
.
Naked
Until the early 1990s, it was widely believed that general relativityGeneral relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
hides every singularity behind an event horizon, making naked singularities impossible. This is referred to as the cosmic censorship hypothesis
Cosmic censorship hypothesis
The weak and the strong cosmic censorship hypotheses are two mathematical conjectures about the structure of singularities arising in general relativity....
. However, in 1991, physicians Stuart Shapiro and Saul Teukolsky
Saul Teukolsky
Saul Teukolsky is a theoretical astrophysicist and a professor of Physics and Astronomy at Cornell University. His major research interests include general relativity, relativistic astrophysics, and computational astrophysics.-Biography:...
performed computer simulations of a rotating plane of dust that indicated that general relativity might allow for "naked" singularities. What these objects would actually look like in such a model is unknown. Nor is it known whether singularities would still arise if the simplifying assumptions used to make the simulation were removed.
Entropy
Before Stephen HawkingStephen Hawking
Stephen William Hawking, CH, CBE, FRS, FRSA is an English theoretical physicist and cosmologist, whose scientific books and public appearances have made him an academic celebrity...
came up with the concept of Hawking radiation, the question of black holes having entropy was avoided. However, this concept demonstrates that black holes can radiate energy, which conserves entropy and solves the incompatibility problems with the second law of thermodynamics. Entropy, however, implies heat and therefore temperature. The loss of energy also suggests that black holes do not last forever, but rather "evaporate" slowly. Small black holes tend to be hotter whereas larger ones tend to be colder. All known black hole candidates are so large that their temperature is far below that of the cosmic background radiation, so they are all gaining energy. They will not begin to lose energy until a cosmological redshift of more than one million is reached, rather than the thousand or so since the background radiation formed.
See also
- Penrose-Hawking singularity theoremsPenrose-Hawking singularity theoremsThe Penrose–Hawking singularity theorems are a set of results in general relativity which attempt to answer the question of when gravitation produces singularities.A singularity in solutions of the Einstein field equations is one of two things:...
- 0-dimensional singularity: magnetic monopoleMagnetic monopoleA magnetic monopole is a hypothetical particle in particle physics that is a magnet with only one magnetic pole . In more technical terms, a magnetic monopole would have a net "magnetic charge". Modern interest in the concept stems from particle theories, notably the grand unified and superstring...
- 1-dimensional singularity: cosmic stringCosmic stringCosmic strings are hypothetical 1-dimensional topological defects which may have formed during a symmetry breaking phase transition in the early universe when the topology of the vacuum manifold associated to this symmetry breaking is not simply connected. It is expected that at least one string...
- 2-dimensional singularity: domain wallDomain wallA domain wall is a term used in physics which can have one of two distinct but similar meanings in magnetism, optics, or string theory. These phenomena can all be generically described as topological solitons which occur whenever a discrete symmetry is spontaneously broken.-Magnetism:In magnetism,...
- Fuzzball (string theory)
Further reading
- The Elegant UniverseThe Elegant UniverseThe Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory is a book by Brian Greene published in 1999, which introduces string and superstring theory, and provides a comprehensive though non-technical assessment of the theory and some of its shortcomings...
by Brian GreeneBrian GreeneBrian Greene is an American theoretical physicist and string theorist. He has been a professor at Columbia University since 1996. Greene has worked on mirror symmetry, relating two different Calabi-Yau manifolds...
. This book provides a layman's introduction to string theory, although some of the views expressed are already becoming outdated. His use of common terms and his providing of examples throughout the text help the layperson understand the basics of string theory.