
Larmor formula
Encyclopedia

Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, in the area of electrodynamics, the Larmor formula (not to be confused with the Larmor precession
Larmor precession
In physics, Larmor precession is the precession of the magnetic moments of electrons, atomic nuclei, and atoms about an external magnetic field...
from classical NMR) is used to calculate the total power
Power (physics)
In physics, power is the rate at which energy is transferred, used, or transformed. For example, the rate at which a light bulb transforms electrical energy into heat and light is measured in watts—the more wattage, the more power, or equivalently the more electrical energy is used per unit...
radiated by a nonrelativistic point charge as it accelerates. It was first derived by J. J. Larmor
Joseph Larmor
Sir Joseph Larmor , a physicist and mathematician who made innovations in the understanding of electricity, dynamics, thermodynamics, and the electron theory of matter...
in 1897, in the context of the wave theory of light.
When accelerating or decelerating, any charged particle (such as an electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
) radiates away energy in the form of electromagnetic waves. For velocities that are small relative to the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
, the total power radiated is given by the Larmor formula:
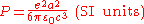
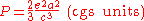
where
 is the acceleration,
is the acceleration,  is the charge, and
is the charge, and  is the speed of light. A relativistic generalization is given by the Liénard-Wiechert Potentials
is the speed of light. A relativistic generalization is given by the Liénard-Wiechert PotentialsLiénard-Wiechert Potentials
Liénard-Wiechert potentials describe the classical electromagnetic effect of a moving electric point charge in terms of a vector potential and a scalar potential...
.
Derivation 1: Mathematical Approach
We first need to find the form of the electric and magnetic fields. The fields can be written (for a fuller derivation see Liénard–Wiechert potential)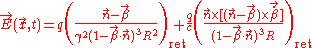
and

where
 is the charge's velocity divided by c,
is the charge's velocity divided by c,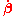 is the acceleration divided by c,
is the acceleration divided by c, is a unit vector in the
is a unit vector in the  direction,
direction, is the magnitude of
is the magnitude of  ,
,and the terms on the right are evaluated at the retarded time
 .
.These field equations divide themselves up into velocity and acceleration fields. The velocity field depends only upon β while the acceleration field depends on both
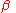 and
and 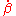 and the angular relationship between the two. Since the velocity field is proportional to
and the angular relationship between the two. Since the velocity field is proportional to 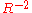 it falls off very quickly with distance. On the other hand, the acceleration field is proportional to
it falls off very quickly with distance. On the other hand, the acceleration field is proportional to 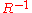 , which means that it falls much more slowly with distance. Because of this, the acceleration field is representative of the radiation field and is responsible for carrying most of the energy away from the charge.
, which means that it falls much more slowly with distance. Because of this, the acceleration field is representative of the radiation field and is responsible for carrying most of the energy away from the charge.We can find the energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
flux
Flux
In the various subfields of physics, there exist two common usages of the term flux, both with rigorous mathematical frameworks.* In the study of transport phenomena , flux is defined as flow per unit area, where flow is the movement of some quantity per time...
density of the radiation field by taking the Poynting vector
Poynting vector
In physics, the Poynting vector can be thought of as representing the directional energy flux density of an electromagnetic field. It is named after its inventor John Henry Poynting. Oliver Heaviside and Nikolay Umov independently co-invented the Poynting vector...
of it;
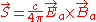
where the 'a' subscripts emphasize that we are taking only the acceleration field. Substituting in the relation between the magnetic and electric fields while assuming that the particle instantaneously at rest at time
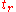 and simplifying gives,
and simplifying gives,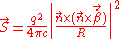
The case where
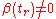 is more difficult (see Griffiths).
is more difficult (see Griffiths).If we let the angle between the acceleration and the observation vector be equal to
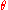 then we can express the above as;
then we can express the above as;
This is actually the power radiated per unit solid angle by the charge. We can therefore calculate the total power by integrating this equation over all solid angles. This gives;
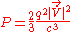
This is the Larmor result for a non-relativistic accelerated charge. It relates the power radiated by the particle to its acceleration. It clearly shows that the faster the charge accelerates the greater the radiation will be. We would expect this since the radiation field is dependent upon acceleration.
Derivation 2: Using Edward M. Purcell approach
The full derivation can be found here.Here is an explanation which can help understanding the above page.
This approach is based on the finite speed of light. A charge moving with
constant velocity has a radial electric field

(at distance

from the charge), always emerging from the future position of the charge,
and there is no tangential component of the electric field
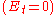 .
.This future position is completely deterministic as long as the velocity
is constant. When the velocity of the charge changes, (say it bounces back
during a short time) the future position "jumps", so from this moment and
on, the radial electric field
 emerges from a new
emerges from a newposition. Given the fact that the electric field must be continuous, a
non-zero tangential component of the electric field
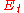 appears,
appears,which decreases like
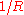 (unlike the radial component which
(unlike the radial component whichdecreases like
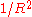 ).
).Hence, at large distances from the charge, the radial component is negligible
relative to the tangential component, and in addition to that, fields which
behave like
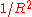 cannot radiate, because the Poynting vector
cannot radiate, because the Poynting vectorassociated with them will behave like
 .
.The tangential component comes out (SI units):
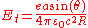 .
.And to obtain the Larmour formula, one has to integrate over all angles, at
large distance
 from the charge, the
from the charge, thePoynting vector
Poynting vector
In physics, the Poynting vector can be thought of as representing the directional energy flux density of an electromagnetic field. It is named after its inventor John Henry Poynting. Oliver Heaviside and Nikolay Umov independently co-invented the Poynting vector...
associated with
 , which is:
, which is: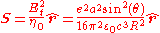
giving (SI units)

This is mathematically equivalent to:
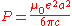
Covariant Form
We can do this by rewriting the Larmor formula in terms of momentum and then using the four vector generalisation of momentum (see four momentum),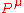 . We know that the power is a Lorentz invariant, so all we have to show is that our generalisation is also invariant and that it reduces to the Larmor formula in the low velocity limit. So;
. We know that the power is a Lorentz invariant, so all we have to show is that our generalisation is also invariant and that it reduces to the Larmor formula in the low velocity limit. So;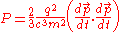
Assume the generalisation;
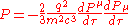
When we expand and rearrange the energy-momentum four vector product we get;
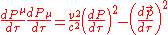
where I have used the fact that
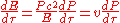 . When you let
. When you let 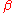 tend to zero,
tend to zero, 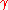 tends to one, so that
tends to one, so that  tends to dt. Thus we recover the non relativistic case.
tends to dt. Thus we recover the non relativistic case.This is an interesting equation. It says that the power radiated by the particle into space depends upon its rate of change of momentum with respect to its time. It also says that the power radiated is proportional to the charge squared and inversely proportional to the mass squared. Thus for a highly charged, extremely small particle the radiation will be much greater than that for a large particle with a small charge.
Non-Covariant Form
To obtain the non-covariant form of the generalisation we first substitute in to the above and then performing the differentiation as follows (for brevity I have omitted the constants from the calculation below);
in to the above and then performing the differentiation as follows (for brevity I have omitted the constants from the calculation below);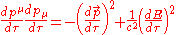
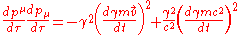
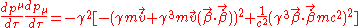
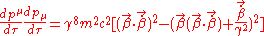
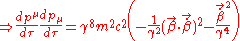
Although the above is correct as it stands, it is not immediately obvious what sort of relationship the radiated power has to the velocity and the acceleration of the particle. If we make this relationship more explicit then it will be clear how the radiation depends on the particle's motion, and what happens in different cases. We can obtain this relation by adding and subtracting
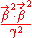 to the above giving;
to the above giving;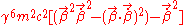
If we apply the vector identity;
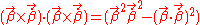
Then we obtain;
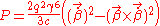
where I have replaced all the constants and the negative sign dropped earlier.
This is the Lienard result, which was first obtained in 1898. The
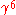 means that when
means that when 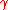 is very close to one (i.e.
is very close to one (i.e.  ) the radiation emitted by the particle is likely to be negligible. However when
) the radiation emitted by the particle is likely to be negligible. However when 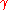 is greater than one (i.e.
is greater than one (i.e.  ) the radiation explodes as the particle tries to lose its energy in the form of EM waves. It's also interesting that when the acceleration and velocity are orthogonal the power is reduced by a factor of
) the radiation explodes as the particle tries to lose its energy in the form of EM waves. It's also interesting that when the acceleration and velocity are orthogonal the power is reduced by a factor of 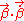 . The faster the motion becomes the greater this reduction gets. In fact, it seems to imply that as
. The faster the motion becomes the greater this reduction gets. In fact, it seems to imply that as 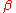 tends to one the power radiated tends to zero (for orthogonal motion). This would suggest that a charge moving at the speed of light, in instantaneously circular motion, emits no radiation. However, it would be impossible to accelerate a charge to this speed because the
tends to one the power radiated tends to zero (for orthogonal motion). This would suggest that a charge moving at the speed of light, in instantaneously circular motion, emits no radiation. However, it would be impossible to accelerate a charge to this speed because the 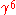 would explode to
would explode to  , meaning that the particle would radiate a gigantic amount of energy which would require you to put more and more energy in to keep accelerating it. This would imply that there is a cosmic speed limit, namely c. Such a connection was not made until 1905 when Einstein published his paper on Special Relativity.
, meaning that the particle would radiate a gigantic amount of energy which would require you to put more and more energy in to keep accelerating it. This would imply that there is a cosmic speed limit, namely c. Such a connection was not made until 1905 when Einstein published his paper on Special Relativity.We can use Lienard's result to predict what sort of radiation losses to expect in different kinds of motion.
Stellar Jets

Radiation reaction
The radiation from a charged particle carries energy and momentum. In order to satisfy energy and momentum conservation, the charged particle must experience a recoil at the time of emission. The radiation must exert an additional force on the charged particle. This force is known as the Abraham-Lorentz forceAbraham-Lorentz force
In the physics of electromagnetism, the Abraham–Lorentz force is the recoil force on an accelerating charged particle caused by the particle emitting electromagnetic radiation. It is also called the radiation reaction force....
in the nonrelativistic limit and the Abraham-Lorentz-Dirac force in the relativistic limit.
Atomic physics
A classical electron orbiting a nucleus experiences acceleration and should radiate. Consequently the electron loses energy and the electron should eventually spiral into the nucleus. Atoms, according to classical mechanics, are consequently unstable. This classical prediction is violated by the observation of stable electron orbits. The problem is resolved with a quantum mechanicalQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
or stochastic electrodynamic
Stochastic electrodynamics
In theoretical physics, Stochastic Electrodynamics is a variant of Classical Electrodynamics which posits the existence of a classical Lorentz Invariant radiation field having statistical properties similar to that of the electromagnetic zero-point field of Quantum Electrodynamics...
description of atomic physics
Atomic physics
Atomic physics is the field of physics that studies atoms as an isolated system of electrons and an atomic nucleus. It is primarily concerned with the arrangement of electrons around the nucleus and...
.
See also
- Atomic theoryAtomic theoryIn chemistry and physics, atomic theory is a theory of the nature of matter, which states that matter is composed of discrete units called atoms, as opposed to the obsolete notion that matter could be divided into any arbitrarily small quantity...
- Cyclotron radiationCyclotron radiationCyclotron radiation is electromagnetic radiation emitted by moving charged particles deflected by a magnetic field. The Lorentz force on the particles acts perpendicular to both the magnetic field lines and the particles' motion through them, creating an acceleration of charged particles that...
- Electromagnetic wave equationElectromagnetic wave equationThe electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a medium or in a vacuum...
- Maxwell's equations in curved spacetimeMaxwell's equations in curved spacetimeIn physics, Maxwell's equations in curved spacetime govern the dynamics of the electromagnetic field in curved spacetime or where one uses an arbitrary coordinate system...
- Radiation reaction
- Wave equationWave equationThe wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...

