Gödel metric
Encyclopedia
The Gödel metric is an exact solution
of the Einstein field equations
in which the stress-energy tensor
contains two terms, the first representing the matter density of a homogeneous distribution of swirling dust particles, and the second associated with a nonzero cosmological constant
(see lambdavacuum solution
). It is also known as the Gödel solution.
This solution has many strange properties, discussed below, in particular the existence of closed timelike curve
s which would allow for a form of time travel
in the type of universe described by the solution. Its definition is somewhat artificial (the value of the cosmological constant must be carefully chosen to match the density of the dust grains), but this spacetime
is regarded as an important pedagogical example.
The solution was found in 1949 by Kurt Gödel
.
in terms of some local coordinate chart. In terms of the original chart, we have

where is a nonzero real constant, which turns out to be the angular velocity, as measured by a nonspinning observer riding any one of the dust grains, of nearby dust grains.
is a nonzero real constant, which turns out to be the angular velocity, as measured by a nonspinning observer riding any one of the dust grains, of nearby dust grains.
(dual to the coframe read off the metric as given above)



This frame defines a family of inertial observers who are comoving with the dust grains. However, computing the Fermi-Walker derivatives with respect to shows that the spatial frames are spinning about
shows that the spatial frames are spinning about  with angular velocity
with angular velocity  . It follows that the nonspinning inertial frame comoving with the dust particles is
. It follows that the nonspinning inertial frame comoving with the dust particles is




Here, the first term is characteristic of a lambdavacuum solution
and the second term is characteristic of a pressureless perfect fluid
or dust solution. Notice that the cosmological constant is carefully chosen to partially cancel the matter density of the dust.
In any Lorentzian spacetime, the fourth-rank Riemann tensor is a multilinear operator on the four dimensional space of tangent vector
s (at some event), but a linear operator on the six-dimensional space of bivector
s at that event. Accordingly it has a characteristic polynomial
, whose roots are the eigenvalues. In the Gödel spacetime, these eigenvalues are extremely simple:
of Killing vectors, which can be generated by time translation , two spatial translations
, two spatial translations  , plus two further Killing vector fields:
, plus two further Killing vector fields:
and .
.
The isometry group acts transitively (since we can translate in , and using the fourth vector we can move along
, and using the fourth vector we can move along  as well), so the spacetime is homogeneous. However, it is not isotropic, as we shall see.
as well), so the spacetime is homogeneous. However, it is not isotropic, as we shall see.
It is obvious from the generators just given that the slices admit a transitive abelian
admit a transitive abelian
three dimensional transformation group, so a quotient of the solution can be reinterpreted as a stationary cylindrically symmetric solution. Less obviously, the slices admit an SL(2,R) action, and the slices
admit an SL(2,R) action, and the slices  admit a Bianchi III (c.f. the fourth Killing vector field). We can restate this by saying that our symmetry group includes as three dimensional subgroups examples of Bianchi types I, III and VIII. Four of the five Killing vectors, as well as the curvature tensor, do not depend upon the coordinate y. Indeed, the Gödel solution is the Cartesian product
admit a Bianchi III (c.f. the fourth Killing vector field). We can restate this by saying that our symmetry group includes as three dimensional subgroups examples of Bianchi types I, III and VIII. Four of the five Killing vectors, as well as the curvature tensor, do not depend upon the coordinate y. Indeed, the Gödel solution is the Cartesian product
of a factor R with a three-dimensional Lorentzian manifold (signature
-++).
It can be shown that the Gödel solution is, up to local isometry, the only perfect fluid solution of the Einstein field equation admitting a five dimensional Lie algebra of Killing vectors.
of the Gödel solution has Petrov type D. This means that for an appropriately chosen observer, the tidal forces have Coulomb form.
To study the tidal forces in more detail, we compute the Bel decomposition
of the Riemann tensor into three pieces, the tidal or electrogravitic tensor (which represents tidal forces), the magnetogravitic tensor (which represents spin-spin forces on spinning test particles and other gravitational effects analogous to magnetism), and the topogravitic tensor (which represents the spatial sectional curvatures).
Interestingly enough, observers comoving with the dust particles find that the tidal tensor (with respect to , which components evaluated in our frame) has the form
, which components evaluated in our frame) has the form
That is, they measure isotropic tidal tension orthogonal to the distinguished direction .
.
The gravitomagnetic tensor vanishes identically
This is an artifact of the unusual symmetries of this spacetime, and implies that the putative "rotation" of the dust does not have the gravitomagnetic effects usually associated with the gravitational field produced by rotating matter.
The principal Lorentz invariants of the Riemann tensor are
The vanishing of the second invariant means that some observers measure no gravitomagnetism, which of course is consistent with what we just said. The fact that the first invariant (the Kretschmann invariant) is constant reflects the homogeneity of the Gödel spacetime.
 , but the vorticity vector of the timelike geodesic congruence defined by the timelike unit vectors is
, but the vorticity vector of the timelike geodesic congruence defined by the timelike unit vectors is
This means that the world lines of nearby dust particles are twisting about one another. Furthermore, the shear tensor of the congruence vanishes, so the dust particles exhibit rigid rotation.
vanishes, so the dust particles exhibit rigid rotation.
of a given observer, we find that null geodesics moving orthogonally to spiral inwards toward the observer, so that if he looks radially, he sees the other dust grains in progressively time-lagged positions. However, the solution is stationary, so it might seem that an observer riding on a dust grain will not see the other grains rotating about himself. However, recall that while the first frame given above (the
spiral inwards toward the observer, so that if he looks radially, he sees the other dust grains in progressively time-lagged positions. However, the solution is stationary, so it might seem that an observer riding on a dust grain will not see the other grains rotating about himself. However, recall that while the first frame given above (the  ) appears static in our chart, the Fermi-Walker derivatives show that, in fact, it is spinning with respect to gyroscopes. The second frame (the
) appears static in our chart, the Fermi-Walker derivatives show that, in fact, it is spinning with respect to gyroscopes. The second frame (the  ) appears to be spinning in our chart, but in fact it is gyrostabilized, and of course a nonspinning inertial observer riding on a dust grain will indeed see the other dust grains rotating clockwise with angular velocity
) appears to be spinning in our chart, but in fact it is gyrostabilized, and of course a nonspinning inertial observer riding on a dust grain will indeed see the other dust grains rotating clockwise with angular velocity  about his axis of symmetry. It turns out that in addition, optical images are expanded and sheared in the direction of rotation.
about his axis of symmetry. It turns out that in addition, optical images are expanded and sheared in the direction of rotation.
If a nonspinning inertial observer looks along his axis of symmetry, he sees his coaxial nonspinning inertial peers apparently nonspinning with respect to himself, as we would expect.
 direction can see only finitely far out, and also see themselves at an earlier time.
direction can see only finitely far out, and also see themselves at an earlier time.
The cusp is a nongeodesic closed null curve. (See the more detailed discussion below using an alternative coordinate chart.)
s (CTC's). Indeed, there are CTCs through every event in the Gödel spacetime. This causal anomaly seems to have been regarded as the whole point of the model by Gödel himself, who was apparently striving to prove, and arguably succeeded in proving, that Einstein's equations of spacetime are not consistent with what we intuitively understand time to be (i.e. that it passes and the past no longer exists, the position philosophers call presentism
, whereas Gödel seems to have been arguing for something more like the philosophy of eternalism), much as he, conversely, succeeded with his Incompleteness Theorems in showing that intuitive mathematical concepts could not be completely described by formal mathematical systems of proof. See the book A World Without Time (ISBN 0465092942).
Einstein was aware of Gödel's solution and commented in Albert Einstein: Philosopher-Scientist that if you can have a series of causally-connected events in which "the series is closed in itself" (in other words, a closed timelike curve), then this suggests that there is no good physical way to define whether a given event in the series happened "earlier" or "later" than another event in the series:
), any such CTC would have to intersect it an odd number of times, contradicting the fact that the spacetime is simply connected. Therefore, this spacetime is not globally hyperbolic
.
Start with a simple frame in a cylindrical type chart, featuring two undetermined functions of the radial coordinate:
Here, we think of the timelike unit vector field as tangent to the world lines of the dust particles, and their world lines will in general exhibit nonzero vorticity but vanishing expansion and shear. Let us demand that the Einstein tensor match a dust term plus a vacuum energy term. This is equivalent to requiring that it match a perfect fluid; i.e., we require that the components of the Einstein tensor, computed with respect to our frame, take the form
as tangent to the world lines of the dust particles, and their world lines will in general exhibit nonzero vorticity but vanishing expansion and shear. Let us demand that the Einstein tensor match a dust term plus a vacuum energy term. This is equivalent to requiring that it match a perfect fluid; i.e., we require that the components of the Einstein tensor, computed with respect to our frame, take the form
This gives the conditions
Plugging these into the Einstein tensor, we see that in fact we now have . The simplest nontrivial spacetime we can construct in this way evidently would have this coefficient be some nonzero but constant function of the radial coordinate. Specifically, with a bit of foresight, let us choose
. The simplest nontrivial spacetime we can construct in this way evidently would have this coefficient be some nonzero but constant function of the radial coordinate. Specifically, with a bit of foresight, let us choose  . This gives
. This gives
Finally, let us demand that this frame satisfy
This gives , and our frame becomes
, and our frame becomes
 , which is of course spacelike for small radii, becomes null at
, which is of course spacelike for small radii, becomes null at  where
where
Here the covector also becomes null (tangent to the light cone). The circle
also becomes null (tangent to the light cone). The circle  is a closed null curve, but not a null geodesic.
is a closed null curve, but not a null geodesic.
Examining the frame above, we can see that the coordinate is inessential; our spacetime is the direct product of a factor R with a signature -++ three-manifold. Suppressing
is inessential; our spacetime is the direct product of a factor R with a signature -++ three-manifold. Suppressing  in order to focus our attention on this three-manifold, let us examine how the appearance of the light cones changes as we travel out from the axis of symmetry
in order to focus our attention on this three-manifold, let us examine how the appearance of the light cones changes as we travel out from the axis of symmetry  :
:
 As we approach the critical radius, the cones become tangent to the coordinate plane
As we approach the critical radius, the cones become tangent to the coordinate plane  , and also become tangent to the closed null curve:
, and also become tangent to the closed null curve:
 , the vector field
, the vector field  becomes null. For larger radii, it is timelike. Thus, corresponding to our symmetry axis we have a timelike congruence made up of circles and corresponding to certain observers. This congruence is however only defined outside the cylinder
becomes null. For larger radii, it is timelike. Thus, corresponding to our symmetry axis we have a timelike congruence made up of circles and corresponding to certain observers. This congruence is however only defined outside the cylinder  .
.
This is not a geodesic congruence; rather, each observer in this family must maintain a constant acceleration in order to hold his course. Observers with smaller radii must accelerate harder; as the magnitude of acceleration diverges, which is of course just what we should expect, given that
the magnitude of acceleration diverges, which is of course just what we should expect, given that  is a null curve.
is a null curve.
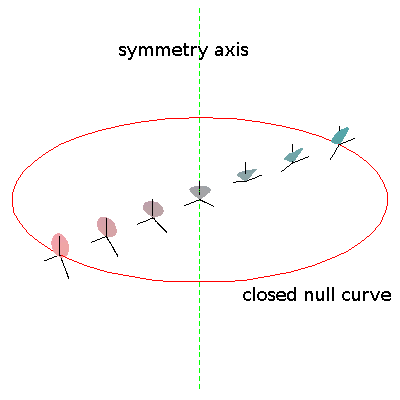
 Recall that vertical coordinate lines in our chart represent the world lines of the dust particles, but despite their straight appearance in our chart, the congruence formed by these curves has nonzero vorticity, so the world lines are actually twisting about each other. The fact that the null geodesics spiral inwards in the manner shown above means that when our observer looks radially outwards, he sees nearby dust particles, not at their current locations, but at their earlier locations. This is just what we would expect if the dust particles are in fact rotating about one another.
Recall that vertical coordinate lines in our chart represent the world lines of the dust particles, but despite their straight appearance in our chart, the congruence formed by these curves has nonzero vorticity, so the world lines are actually twisting about each other. The fact that the null geodesics spiral inwards in the manner shown above means that when our observer looks radially outwards, he sees nearby dust particles, not at their current locations, but at their earlier locations. This is just what we would expect if the dust particles are in fact rotating about one another.
Note that the null geodesics are of course geometrically straight; in the figure, they appear to be spirals only because the coordinates are "rotating" in order to permit the dust particles to appear stationary.
 This implies that in the Gödel lambdadust solution, the absolute future of each event has a character very different from what we might naively expect!
This implies that in the Gödel lambdadust solution, the absolute future of each event has a character very different from what we might naively expect!
We have seen that observers lying on the y axis (in the original chart) see the rest of the universe rotating clockwise about that axis. However, the homogeneity of the spacetime shows that the direction but not the position of this "axis" is distinguished.
Some have interpreted the Gödel universe as a counterexample to Einstein's hopes that general relativity should exhibit some kind of Mach principle
, citing the fact that the matter is rotating (world lines twisting about each other) in a manner sufficient to pick out a preferred direction, although with no distinguished axis of rotation.
Others take Mach principle to mean some physical law tying the definition of nonspinning inertial frames at each event to the global distribution and motion of matter everywhere in the universe, and say that because the nonspinning inertial frames are precisely tied to the rotation of the dust in just the way such a Mach principle would suggest, this model does accord with Mach's ideas.
Many other exact solutions which can be interpreted as cosmological models of rotating universes are known. See the book by Ryan and Shepley for some of these generalizations.
Exact solutions in general relativity
In general relativity, an exact solution is a Lorentzian manifold equipped with certain tensor fields which are taken to model states of ordinary matter, such as a fluid, or classical nongravitational fields such as the electromagnetic field....
of the Einstein field equations
Einstein field equations
The Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
in which the stress-energy tensor
Stress-energy tensor
The stress–energy tensor is a tensor quantity in physics that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields...
contains two terms, the first representing the matter density of a homogeneous distribution of swirling dust particles, and the second associated with a nonzero cosmological constant
Cosmological constant
In physical cosmology, the cosmological constant was proposed by Albert Einstein as a modification of his original theory of general relativity to achieve a stationary universe...
(see lambdavacuum solution
Lambdavacuum solution
In general relativity, a lambdavacuum solution is an exact solution to the Einstein field equation in which the only term in the stress-energy tensor is a cosmological constant term...
). It is also known as the Gödel solution.
This solution has many strange properties, discussed below, in particular the existence of closed timelike curve
Closed timelike curve
In mathematical physics, a closed timelike curve is a worldline in a Lorentzian manifold, of a material particle in spacetime that is "closed," returning to its starting point...
s which would allow for a form of time travel
Time travel
Time travel is the concept of moving between different points in time in a manner analogous to moving between different points in space. Time travel could hypothetically involve moving backward in time to a moment earlier than the starting point, or forward to the future of that point without the...
in the type of universe described by the solution. Its definition is somewhat artificial (the value of the cosmological constant must be carefully chosen to match the density of the dust grains), but this spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
is regarded as an important pedagogical example.
The solution was found in 1949 by Kurt Gödel
Kurt Gödel
Kurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
.
Definition
Like any other Lorentzian spacetime, the Gödel solution is defined by giving the metric tensorMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
in terms of some local coordinate chart. In terms of the original chart, we have


where
 is a nonzero real constant, which turns out to be the angular velocity, as measured by a nonspinning observer riding any one of the dust grains, of nearby dust grains.
is a nonzero real constant, which turns out to be the angular velocity, as measured by a nonspinning observer riding any one of the dust grains, of nearby dust grains.Properties
To study the properties of the Gödel solution, we can adopt the frame fieldFrame fields in general relativity
In general relativity, a frame field is a set of four orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime...
(dual to the coframe read off the metric as given above)




This frame defines a family of inertial observers who are comoving with the dust grains. However, computing the Fermi-Walker derivatives with respect to
 shows that the spatial frames are spinning about
shows that the spatial frames are spinning about  with angular velocity
with angular velocity  . It follows that the nonspinning inertial frame comoving with the dust particles is
. It follows that the nonspinning inertial frame comoving with the dust particles is



Einstein tensor
The components of the Einstein tensor (with respect to either frame above) are
Here, the first term is characteristic of a lambdavacuum solution
Lambdavacuum solution
In general relativity, a lambdavacuum solution is an exact solution to the Einstein field equation in which the only term in the stress-energy tensor is a cosmological constant term...
and the second term is characteristic of a pressureless perfect fluid
Perfect fluid
In physics, a perfect fluid is a fluid that can be completely characterized by its rest frame energy density ρ and isotropic pressure p....
or dust solution. Notice that the cosmological constant is carefully chosen to partially cancel the matter density of the dust.
Topology
The Gödel spacetime is a rare example of a regular (singularity-free) solution of the Einstein field equation. The chart given here (the original chart of Gödel) is geodesically complete but singularity free; therefore, it is a global chart, and the spacetime is diffeomorphic to R4, and therefore simply connected.Invariants
The curvature invariants of the Gödel spacetime are remarkable. We'll mention just one feature.In any Lorentzian spacetime, the fourth-rank Riemann tensor is a multilinear operator on the four dimensional space of tangent vector
Tangent vector
A tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....
s (at some event), but a linear operator on the six-dimensional space of bivector
Bivector
In mathematics, a bivector or 2-vector is a quantity in geometric algebra or exterior algebra that generalises the idea of a vector. If a scalar is considered a zero dimensional quantity, and a vector is a one dimensional quantity, then a bivector can be thought of as two dimensional. Bivectors...
s at that event. Accordingly it has a characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
, whose roots are the eigenvalues. In the Gödel spacetime, these eigenvalues are extremely simple:
- triple eigenvalue zero,
- double eigenvalue -
 ,
, - simple eigenvalue
 .
.
Killing vectors
This spacetime admits a remarkable five dimensional Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of Killing vectors, which can be generated by time translation
 , two spatial translations
, two spatial translations  , plus two further Killing vector fields:
, plus two further Killing vector fields:
and
 .
.The isometry group acts transitively (since we can translate in
 , and using the fourth vector we can move along
, and using the fourth vector we can move along  as well), so the spacetime is homogeneous. However, it is not isotropic, as we shall see.
as well), so the spacetime is homogeneous. However, it is not isotropic, as we shall see.It is obvious from the generators just given that the slices
 admit a transitive abelian
admit a transitive abelianAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
three dimensional transformation group, so a quotient of the solution can be reinterpreted as a stationary cylindrically symmetric solution. Less obviously, the slices
 admit an SL(2,R) action, and the slices
admit an SL(2,R) action, and the slices  admit a Bianchi III (c.f. the fourth Killing vector field). We can restate this by saying that our symmetry group includes as three dimensional subgroups examples of Bianchi types I, III and VIII. Four of the five Killing vectors, as well as the curvature tensor, do not depend upon the coordinate y. Indeed, the Gödel solution is the Cartesian product
admit a Bianchi III (c.f. the fourth Killing vector field). We can restate this by saying that our symmetry group includes as three dimensional subgroups examples of Bianchi types I, III and VIII. Four of the five Killing vectors, as well as the curvature tensor, do not depend upon the coordinate y. Indeed, the Gödel solution is the Cartesian productCartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of a factor R with a three-dimensional Lorentzian manifold (signature
Signature
A signature is a handwritten depiction of someone's name, nickname, or even a simple "X" that a person writes on documents as a proof of identity and intent. The writer of a signature is a signatory. Similar to a handwritten signature, a signature work describes the work as readily identifying...
-++).
It can be shown that the Gödel solution is, up to local isometry, the only perfect fluid solution of the Einstein field equation admitting a five dimensional Lie algebra of Killing vectors.
Petrov type and Bel decomposition
The Weyl tensorWeyl tensor
In differential geometry, the Weyl curvature tensor, named after Hermann Weyl, is a measure of the curvature of spacetime or, more generally, a pseudo-Riemannian manifold. Like the Riemann curvature tensor, the Weyl tensor expresses the tidal force that a body feels when moving along a geodesic...
of the Gödel solution has Petrov type D. This means that for an appropriately chosen observer, the tidal forces have Coulomb form.
To study the tidal forces in more detail, we compute the Bel decomposition
Bel decomposition
In semi-Riemannian geometry, the Bel decomposition, taken with respect to a specific timelike congruence, is a way of breaking up the Riemann tensor of a pseudo-Riemannian manifold into four pieces. It was introduced in 1959 by the physicist Lluis Bel....
of the Riemann tensor into three pieces, the tidal or electrogravitic tensor (which represents tidal forces), the magnetogravitic tensor (which represents spin-spin forces on spinning test particles and other gravitational effects analogous to magnetism), and the topogravitic tensor (which represents the spatial sectional curvatures).
Interestingly enough, observers comoving with the dust particles find that the tidal tensor (with respect to
 , which components evaluated in our frame) has the form
, which components evaluated in our frame) has the form
That is, they measure isotropic tidal tension orthogonal to the distinguished direction
 .
.The gravitomagnetic tensor vanishes identically

This is an artifact of the unusual symmetries of this spacetime, and implies that the putative "rotation" of the dust does not have the gravitomagnetic effects usually associated with the gravitational field produced by rotating matter.
The principal Lorentz invariants of the Riemann tensor are

The vanishing of the second invariant means that some observers measure no gravitomagnetism, which of course is consistent with what we just said. The fact that the first invariant (the Kretschmann invariant) is constant reflects the homogeneity of the Gödel spacetime.
Rigid rotation
The frame fields given above are both inertial, , but the vorticity vector of the timelike geodesic congruence defined by the timelike unit vectors is
, but the vorticity vector of the timelike geodesic congruence defined by the timelike unit vectors is
This means that the world lines of nearby dust particles are twisting about one another. Furthermore, the shear tensor of the congruence
 vanishes, so the dust particles exhibit rigid rotation.
vanishes, so the dust particles exhibit rigid rotation.Optical effects
If we study the past light coneLight cone
A light cone is the path that a flash of light, emanating from a single event and traveling in all directions, would take through spacetime...
of a given observer, we find that null geodesics moving orthogonally to
 spiral inwards toward the observer, so that if he looks radially, he sees the other dust grains in progressively time-lagged positions. However, the solution is stationary, so it might seem that an observer riding on a dust grain will not see the other grains rotating about himself. However, recall that while the first frame given above (the
spiral inwards toward the observer, so that if he looks radially, he sees the other dust grains in progressively time-lagged positions. However, the solution is stationary, so it might seem that an observer riding on a dust grain will not see the other grains rotating about himself. However, recall that while the first frame given above (the  ) appears static in our chart, the Fermi-Walker derivatives show that, in fact, it is spinning with respect to gyroscopes. The second frame (the
) appears static in our chart, the Fermi-Walker derivatives show that, in fact, it is spinning with respect to gyroscopes. The second frame (the  ) appears to be spinning in our chart, but in fact it is gyrostabilized, and of course a nonspinning inertial observer riding on a dust grain will indeed see the other dust grains rotating clockwise with angular velocity
) appears to be spinning in our chart, but in fact it is gyrostabilized, and of course a nonspinning inertial observer riding on a dust grain will indeed see the other dust grains rotating clockwise with angular velocity  about his axis of symmetry. It turns out that in addition, optical images are expanded and sheared in the direction of rotation.
about his axis of symmetry. It turns out that in addition, optical images are expanded and sheared in the direction of rotation.If a nonspinning inertial observer looks along his axis of symmetry, he sees his coaxial nonspinning inertial peers apparently nonspinning with respect to himself, as we would expect.
Shape of absolute future
According to Hawking and Ellis, another remarkable feature of this spacetime is the fact that, if we suppress the inessential y coordinate, light emitted from an event on the world line of a given dust particle spirals outwards, forms a circular cusp, then spirals inward and reconverges at a subsequent event on the world line of the original dust particle. This means that observers looking orthogonally to the direction can see only finitely far out, and also see themselves at an earlier time.
direction can see only finitely far out, and also see themselves at an earlier time.The cusp is a nongeodesic closed null curve. (See the more detailed discussion below using an alternative coordinate chart.)
Closed timelike curves
Because of the homogeneity of the spacetime and the mutual twisting of our family of timelike geodesics, it is more or less inevitable that the Gödel spacetime should have closed timelike curveClosed timelike curve
In mathematical physics, a closed timelike curve is a worldline in a Lorentzian manifold, of a material particle in spacetime that is "closed," returning to its starting point...
s (CTC's). Indeed, there are CTCs through every event in the Gödel spacetime. This causal anomaly seems to have been regarded as the whole point of the model by Gödel himself, who was apparently striving to prove, and arguably succeeded in proving, that Einstein's equations of spacetime are not consistent with what we intuitively understand time to be (i.e. that it passes and the past no longer exists, the position philosophers call presentism
Presentism (philosophy of time)
Saint Augustine proposed that the present is a knife edge between the past and the future and could not contain any extended period of time. This seems evident because, if the present is extended, it must have separate parts - but these must be simultaneous if they are truly part of the present...
, whereas Gödel seems to have been arguing for something more like the philosophy of eternalism), much as he, conversely, succeeded with his Incompleteness Theorems in showing that intuitive mathematical concepts could not be completely described by formal mathematical systems of proof. See the book A World Without Time (ISBN 0465092942).
Einstein was aware of Gödel's solution and commented in Albert Einstein: Philosopher-Scientist that if you can have a series of causally-connected events in which "the series is closed in itself" (in other words, a closed timelike curve), then this suggests that there is no good physical way to define whether a given event in the series happened "earlier" or "later" than another event in the series:
In that case the distinction “earlier-later” is abandoned for world-points which lie far apart in a cosmological sense, and those paradoxes, regarding the direction of the causal connection, arise, of which Mr. Gödel has spoken.
Such cosmological solutions of the gravitation-equations (with not vanishing A-constant) have been found by Mr. Gödel. It will be interesting to weigh whether these are not to be excluded on physical grounds.
Globally nonhyperbolic
If the Gödel spacetime admitted any boundaryless spatial hyperslices (e.g. a Cauchy surfaceCauchy surface
Intuitively, a Cauchy surface is a plane in space-time which is like an instant of time; its significance is that giving the initial conditions on this plane determines the future uniquely....
), any such CTC would have to intersect it an odd number of times, contradicting the fact that the spacetime is simply connected. Therefore, this spacetime is not globally hyperbolic
Globally hyperbolic
In mathematical physics, a spacetime manifold is globally hyperbolic if it satisfies a condition related to its causal structure. This is relevant to Einstein's theory of general relativity, and potentially to other metric gravitational theories....
.
A cylindrical chart
In this section, we introduce another coordinate chart for the Gödel solution, in which some of the features mentioned above are easier to see.Derivation
Gödel did not explain how he found his solution, but there are in fact many possible derivations. We will sketch one here, and at the same time verify some of the claims made above.Start with a simple frame in a cylindrical type chart, featuring two undetermined functions of the radial coordinate:

Here, we think of the timelike unit vector field
 as tangent to the world lines of the dust particles, and their world lines will in general exhibit nonzero vorticity but vanishing expansion and shear. Let us demand that the Einstein tensor match a dust term plus a vacuum energy term. This is equivalent to requiring that it match a perfect fluid; i.e., we require that the components of the Einstein tensor, computed with respect to our frame, take the form
as tangent to the world lines of the dust particles, and their world lines will in general exhibit nonzero vorticity but vanishing expansion and shear. Let us demand that the Einstein tensor match a dust term plus a vacuum energy term. This is equivalent to requiring that it match a perfect fluid; i.e., we require that the components of the Einstein tensor, computed with respect to our frame, take the form
This gives the conditions

Plugging these into the Einstein tensor, we see that in fact we now have
 . The simplest nontrivial spacetime we can construct in this way evidently would have this coefficient be some nonzero but constant function of the radial coordinate. Specifically, with a bit of foresight, let us choose
. The simplest nontrivial spacetime we can construct in this way evidently would have this coefficient be some nonzero but constant function of the radial coordinate. Specifically, with a bit of foresight, let us choose  . This gives
. This gives
Finally, let us demand that this frame satisfy

This gives
 , and our frame becomes
, and our frame becomes
Appearance of the light cones
From the metric tensor we find that the vector field , which is of course spacelike for small radii, becomes null at
, which is of course spacelike for small radii, becomes null at  where
where
Here the covector
 also becomes null (tangent to the light cone). The circle
also becomes null (tangent to the light cone). The circle  is a closed null curve, but not a null geodesic.
is a closed null curve, but not a null geodesic.Examining the frame above, we can see that the coordinate
 is inessential; our spacetime is the direct product of a factor R with a signature -++ three-manifold. Suppressing
is inessential; our spacetime is the direct product of a factor R with a signature -++ three-manifold. Suppressing  in order to focus our attention on this three-manifold, let us examine how the appearance of the light cones changes as we travel out from the axis of symmetry
in order to focus our attention on this three-manifold, let us examine how the appearance of the light cones changes as we travel out from the axis of symmetry  :
:
 , and also become tangent to the closed null curve:
, and also become tangent to the closed null curve:
A congruence of closed timelike curves
At the critical radius , the vector field
, the vector field  becomes null. For larger radii, it is timelike. Thus, corresponding to our symmetry axis we have a timelike congruence made up of circles and corresponding to certain observers. This congruence is however only defined outside the cylinder
becomes null. For larger radii, it is timelike. Thus, corresponding to our symmetry axis we have a timelike congruence made up of circles and corresponding to certain observers. This congruence is however only defined outside the cylinder  .
.This is not a geodesic congruence; rather, each observer in this family must maintain a constant acceleration in order to hold his course. Observers with smaller radii must accelerate harder; as
 the magnitude of acceleration diverges, which is of course just what we should expect, given that
the magnitude of acceleration diverges, which is of course just what we should expect, given that  is a null curve.
is a null curve.Null geodesics
If we examine the past light cone of an event on the axis of symmetry, we find the following picture:
Note that the null geodesics are of course geometrically straight; in the figure, they appear to be spirals only because the coordinates are "rotating" in order to permit the dust particles to appear stationary.
The absolute future
According to Hawking and Ellis (see monograph cited below), all light rays emitted from an event on the symmetry axis reconverge at a later event on the axis, with the null geodesics forming a circular cusp (which is a null curve, but not a null geodesic):
Cosmological Interpretation
Following Gödel, we can interpret the dust particles as galaxies, so that the Gödel solution becomes a cosmological model of a rotating universe. Besides rotating, this model exhibits no Hubble expansion, so it is not a realistic model of the universe in which we live, but can be taken as illustrating an alternative universe which would in principle be allowed by general relativity (if one admits the legitimacy of a nonzero cosmological constant). A less well known solution of Godel's exhibits both rotation and Hubble expansion, and has the other qualities of his first model, so Godel's model is really killed by the inconvenient observations that the universe is not rotating. The quality of these observations improved continually up until his death, and he would always ask "is the universe rotating yet?" and be told "no, it isn't."We have seen that observers lying on the y axis (in the original chart) see the rest of the universe rotating clockwise about that axis. However, the homogeneity of the spacetime shows that the direction but not the position of this "axis" is distinguished.
Some have interpreted the Gödel universe as a counterexample to Einstein's hopes that general relativity should exhibit some kind of Mach principle
Mach's principle
In theoretical physics, particularly in discussions of gravitation theories, Mach's principle is the name given by Einstein to an imprecise hypothesis often credited to the physicist and philosopher Ernst Mach....
, citing the fact that the matter is rotating (world lines twisting about each other) in a manner sufficient to pick out a preferred direction, although with no distinguished axis of rotation.
Others take Mach principle to mean some physical law tying the definition of nonspinning inertial frames at each event to the global distribution and motion of matter everywhere in the universe, and say that because the nonspinning inertial frames are precisely tied to the rotation of the dust in just the way such a Mach principle would suggest, this model does accord with Mach's ideas.
Many other exact solutions which can be interpreted as cosmological models of rotating universes are known. See the book by Ryan and Shepley for some of these generalizations.
See also
- van Stockum dustVan Stockum dustIn general relativity, the van Stockum dust is an exact solution of the Einstein field equation in which the gravitational field is generated by dust rotating about an axis of cylindrical symmetry...
, for another rotating dust solution with (true) cylindrical symmetry, - dust solutionDust solutionIn general relativity, a dust solution is an exact solution of the Einstein field equation in which the gravitational field is produced entirely by the mass, momentum, and stress density of a perfect fluid which has positive mass density but vanishing pressure...
, an article about dust solutions in general relativity.

