
Dust solution
Encyclopedia
In general relativity
, a dust solution is an exact solution
of the Einstein field equation in which the gravitational field is produced entirely by the mass, momentum, and stress density of a perfect fluid
which has positive mass density but vanishing pressure. Dust solutions are by far the most important special case of fluid solution
s in general relativity.
The pressureless perfect fluid in a dust solution can be interpreted as a model of a configuration of dust particles which interact with each other only gravitationally. For this reason, dust models are often employed in cosmology
as models of a toy universe, in which the dust particles are considered as highly idealized models of galaxies, clusters, or superclusters. In astrophysics
, dust solutions have been employed as models of gravitational collapse
.
Dust solutions can also be used to model finite rotating disks of dust grains; some fascinating examples are known (see list below). If superimposed somehow on a stellar model comprising a ball of fluid surrounded by vacuum, a dust solution could be used to model an accretion disk around a massive object; however, no such exact solutions modeling rotating accretion disks are yet known due to the extreme mathematical difficulty of constructing them.
of a relativistic pressureless fluid can be written in the simple form
Here

of the Einstein tensor in a dust solution must have the form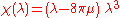
Multiplying out this product, we find that the coefficients must satisfy the following three algebraically independent (and invariant) conditions:
Using Newton's identities
, in terms of the sums of the powers of the roots (eigenvalues), which are also the traces of the powers of the Einstein tensor itself, these conditions become: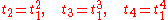
In tensor gymnastics notation, this can be written using the Ricci scalar as:
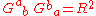

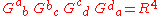
This eigenvalue criterion is sometimes useful in searching for dust solutions, since it shows that very few Lorentzian manifolds could possibly admit an interpretation, in general relativity, as a dust solution.
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, a dust solution is an exact solution
Exact solutions in general relativity
In general relativity, an exact solution is a Lorentzian manifold equipped with certain tensor fields which are taken to model states of ordinary matter, such as a fluid, or classical nongravitational fields such as the electromagnetic field....
of the Einstein field equation in which the gravitational field is produced entirely by the mass, momentum, and stress density of a perfect fluid
Perfect fluid
In physics, a perfect fluid is a fluid that can be completely characterized by its rest frame energy density ρ and isotropic pressure p....
which has positive mass density but vanishing pressure. Dust solutions are by far the most important special case of fluid solution
Fluid solution
In general relativity, a fluid solution is an exact solution of the Einstein field equation in which the gravitational field is produced entirely by the mass, momentum, and stress density of a fluid....
s in general relativity.
The pressureless perfect fluid in a dust solution can be interpreted as a model of a configuration of dust particles which interact with each other only gravitationally. For this reason, dust models are often employed in cosmology
Physical cosmology
Physical cosmology, as a branch of astronomy, is the study of the largest-scale structures and dynamics of the universe and is concerned with fundamental questions about its formation and evolution. For most of human history, it was a branch of metaphysics and religion...
as models of a toy universe, in which the dust particles are considered as highly idealized models of galaxies, clusters, or superclusters. In astrophysics
Astrophysics
Astrophysics is the branch of astronomy that deals with the physics of the universe, including the physical properties of celestial objects, as well as their interactions and behavior...
, dust solutions have been employed as models of gravitational collapse
Gravitational collapse
Gravitational collapse is the inward fall of a body due to the influence of its own gravity. In any stable body, this gravitational force is counterbalanced by the internal pressure of the body, in the opposite direction to the force of gravity...
.
Dust solutions can also be used to model finite rotating disks of dust grains; some fascinating examples are known (see list below). If superimposed somehow on a stellar model comprising a ball of fluid surrounded by vacuum, a dust solution could be used to model an accretion disk around a massive object; however, no such exact solutions modeling rotating accretion disks are yet known due to the extreme mathematical difficulty of constructing them.
Mathematical definition
The stress-energy tensorStress-energy tensor
The stress–energy tensor is a tensor quantity in physics that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields...
of a relativistic pressureless fluid can be written in the simple form

Here
- the world lines of the dust particles are the integral curves of the velocity vectorFour-velocityIn physics, in particular in special relativity and general relativity, the four-velocity of an object is a four-vector that replaces classicalvelocity...
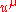 ,
, - the matter density is given by the scalar function
 .
.
Eigenvalues
The characteristic polynomialCharacteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....

of the Einstein tensor in a dust solution must have the form
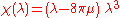
Multiplying out this product, we find that the coefficients must satisfy the following three algebraically independent (and invariant) conditions:

Using Newton's identities
Newton's identities
In mathematics, Newton's identities, also known as the Newton–Girard formulae, give relations between two types of symmetric polynomials, namely between power sums and elementary symmetric polynomials...
, in terms of the sums of the powers of the roots (eigenvalues), which are also the traces of the powers of the Einstein tensor itself, these conditions become:
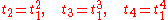
In tensor gymnastics notation, this can be written using the Ricci scalar as:

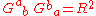

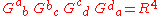
This eigenvalue criterion is sometimes useful in searching for dust solutions, since it shows that very few Lorentzian manifolds could possibly admit an interpretation, in general relativity, as a dust solution.
Examples
Noteworthy individual dust solutions include:- FLRW dusts (homogeneous and isotropic solutions often referred to as the matter-dominated FLRW models)
- Kasner dusts (the simplest cosmological model exhibiting anisotropic expansion)
- Bianchi dust models (generalizations of FLRW and Kasner models, exhibiting various types of Lie algebras of Killing vector fields)
- LTB dusts (some of the simplest inhomogeneous cosmological models, often employed as models of gravitational collapse)
- Kantowski-Sachs dusts (cosmological models which exhibit perturbationsPerturbation (astronomy)Perturbation is a term used in astronomy in connection with descriptions of the complex motion of a massive body which is subject to appreciable gravitational effects from more than one other massive body....
from FLRW models) - van Stockum dustVan Stockum dustIn general relativity, the van Stockum dust is an exact solution of the Einstein field equation in which the gravitational field is generated by dust rotating about an axis of cylindrical symmetry...
(a cylindrically symmetric rotating dust) - the Neugebauer-Meinel dust (which models a rotating disk of dust matched to an axisymmetric vacuum exterior; this solution has been called, with some justice, the most remarkable exact solution discovered since the Kerr vacuum)
- Gödel metricGödel metricThe Gödel metric is an exact solution of the Einstein field equations in which the stress-energy tensor contains two terms, the first representing the matter density of a homogeneous distribution of swirling dust particles, and the second associated with a nonzero cosmological constant...
See also
- Exact solutions in general relativityExact solutions in general relativityIn general relativity, an exact solution is a Lorentzian manifold equipped with certain tensor fields which are taken to model states of ordinary matter, such as a fluid, or classical nongravitational fields such as the electromagnetic field....
, for exact solutions in general, - Fluid solutionFluid solutionIn general relativity, a fluid solution is an exact solution of the Einstein field equation in which the gravitational field is produced entirely by the mass, momentum, and stress density of a fluid....
, for perfect fluid solutions in general relativity (a generalization of dust solutions), - Lorentz groupLorentz groupIn physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...

