Type theory
Encyclopedia
In mathematics
, logic
and computer science
, type theory is any of several formal systems that can serve as alternatives to naive set theory
, or the study of such formalisms in general. In programming language theory
, a branch of computer science
, type theory can refer to the design, analysis and study of type system
s, although some computer scientists limit the term's meaning to the study of abstract formalisms such as typed λ-calculi
.
Bertrand Russell
invented the first type theory in response to his discovery that Gottlob Frege
's version of naive set theory
was afflicted with Russell's paradox
. This theory of types features prominently in Whitehead
and Russell
's Principia Mathematica
. It avoids Russell's paradox by first creating a hierarchy of types, then assigning each mathematical (and possibly other) entity to a type. Objects of a given type are built exclusively from objects of preceding types (those lower in the hierarchy), thus preventing loops.
Alonzo Church
, inventor of the lambda calculus
, developed a higher-order logic
commonly called Church's Theory of Types, in order to avoid the Kleene–Rosser paradox afflicting the original pure lambda calculus. Church's type theory is a variant of the lambda calculus in which expressions (also called formulas or λ-terms) are classified into types, and the types of expressions restrict the ways in which they can be combined. In other words, it is a typed lambda calculus
.
The article Church's Type Theory
in the Stanford Encyclopedia of Philosophy
is devoted to this subject.
Today many other such calculi are in use, including Per Martin-Löf
's Intuitionistic type theory
, Jean-Yves Girard
's System F
and the Calculus of Constructions
. In typed lambda calculi, types play a role similar to that of sets in set theory
.
(1902) Russell announced his discovery of the paradox in Frege's Begriffsschrift
. Frege promptly responded, acknowledging the problem and proposing a solution in a technical discussion of "levels". To quote Frege:
He goes about showing how this might work but seems to pull back from it. (In a footnote, van Heijenoort notes that in Frege 1893 Frege had used a symbol (horseshoe) "for reducing second-level functions to first-level functions"). As a consequence of what has become known as Russell's paradox
both Frege and Russell had to quickly emend works that they had at the printers. In an Appendix B that Russell tacked on to his 1903 Principles of Mathematics one finds his "tentative" "theory of types".
The matter plagued Russell for about five years (1903–1908). Willard Quine in his preface to Russell's (1908a) Mathematical logic as based on the theory of types presents a historical synopsis of the origin of the theory of types and the "ramified" theory of types: Russell proposed in turn a number of alternatives: (i) abandoning the theory of types (1905) followed by three theories in 1905: (ii.1) the zigzag theory, (ii.2) theory of limitation of size, (ii.3) the no-class theory (1905–1906), then (iii) readopting the theory of types (1908ff)".
Quine observes that Russell's introduction of the notion of "apparent variable" had the following result: "the distinction between 'all' and 'any': 'all' is expressed by the bound ('apparent') variable of universal quantification, which ranges over a type, and 'any' is expressed by the free ('real') variable which refers schematically to any unspecified thing irrespective of type". Quine dismisses this notion of "bound variable" as "pointless apart from a certain aspect of the theory of types".
. By 1910 Whitehead and Russell in their Principia Mathematica would further augment this axiom with the notion of a matrix -- a fully extensional specification of a function. From its matrix a function could be derived by the process of "generalization" and vice versa, i.e. the two processes are reversible -- (i) generalization from a matrix to a function ( by use apparent variables ) and (ii) the reverse process of reduction of type by courses-of-values substitution of arguments for the apparent variable. By this method impredicativity could be avoided.
s of different kinds, and as a result necessitates the cumbersome theory of types, this subtheory uses only real variables, and these real variables represent but one kind of entity, which the authors have chosen to call elementary propositions".
At about the same time Ludwig Wittgenstein
made short work of the theory of types in his 1922 work Tractatus Logico-Philosophicus
in which he points out the following in parts 3.331–3.333:
Wittgenstein proposed the truth-table method as well. In his 4.3 through 5.101, Wittgenstein adopts an unbounded Sheffer stroke
as his fundamental logical entity and then lists all 16 functions of two variables (5.101).
The notion of matrix-as-truth-table appears as late as the 1940-1950's in the work of Tarski, e.g. his 1946 indexes "Matrix, see: Truth table"
Russell abandons the axiom of reducibility: In the second edition of Principia Mathematica (1927) he acknowledges Wittgenstein's argument. At the outset of his Introduction he declares "there can be no doubt ... that there is no need of the distinction between real and apparent variables...". Now he fully embraces the matrix notion and declares "A function can only appear in a matrix through its values" (but demurs in a footnote: "It takes the place (not quite adequately) of the axiom of reducibility"). Furthermore, he introduces a new (abbreviated, generalized) notion of "matrix", that of a "logical matrix . . . one that contains no constants. Thus p|q is a logical matrix". Thus Russell has virtually abandoned the axiom of reducibility, but in his last paragraphs he states that from "our present primitive propositions" he cannot derive "Dedekindian relations and well-ordered relations" and observes that if there is a new axiom to replace the axiom of reducibility "it remains to be discovered".
and Frank P. Ramsey
noticed that, if one is willing to give up the vicious circle principle
,
the hierarchy of levels of types in the "ramified theory of types" (see the History section for more on this) can be collapsed.
The resulting restricted logic is called the theory of simple types or, perhaps more commonly, simple type theory. Detailed formulations of simple type theory were published in the late 1920s and early 1930s
by R. Carnap, F. Ramsey, W.V.O. Quine, and A. Tarski. In 1940 Alonzo Church
(re)formulated it as simply typed lambda calculus
. and examined by Gödel in his 1944.
in his 1944 Russell's mathematical logic gave the following definition of the "theory of simple types" in a footnote:
He concluded the (1) theory of simple types and (2) axiomatic set theory, "permit the derivation of modern mathematics and at the same time avoid all known paradoxes" (Gödel 1944:126); furthermore, the theory of simple types "is the system of the first Prinicipa [Principia Mathematica] in an appropriate interpretation. . . . [However}, many symptoms show only too clearly, however, that the primitive concepts need further elucidation" (Gödel 1944:126).
ST is equivalent with Russell's ramified theory plus the Axiom of reducibility
.
The domain of quantification
is partitioned into an ascending hierarchy of types, with all individual
s assigned a type. Quantified variables range over only one type; hence the underlying logic is first-order logic
. ST is "simple" (relative to the type theory of Principia Mathematica
) primarily because all members of the domain
and codomain
of any relation
must be of the same type.
There is a lowest type, whose individuals have no members and are members of the second lowest type. Individuals of the lowest type correspond to the urelements of certain set theories. Each type has a next higher type, analogous to the notion of successor in Peano arithmetic. While ST is silent as to whether there is a maximal type, a transfinite number of types poses no difficulty. These facts, reminiscent of the Peano axioms, make it convenient and conventional to assign a natural number
to each type, starting with 0 for the lowest type. But type theory does not require a prior definition of the naturals.
The symbols peculiar to ST are primed variables and infix
. In any given formula, unprimed variables all have the same type, while primed variables (
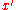) range over the next higher type. The atomic formula
s of ST are of two forms,
(identity
) and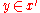
. The infix
symbol
suggests the intended interpretation
, set membership.
All variables appearing in the definition of identity and in the axioms Extensionality and Comprehension, range over individuals of one of two consecutive types. Only unprimed variables (ranging over the "lower" type) can appear to the left of '
', where as to its right, only primed variables (ranging over the "higher" type) can appear. The first-order formulation of ST rules out quantifying over types. Hence each pair of consecutive types requires its own axiom of Extensionality and of Comprehension, which is possible if Extensionality and Comprehension below are taken as axiom schemata "ranging over" types.
ST reveals how type theory can be made very similar to axiomatic set theory. Moreover, the more elaborate ontology of ST, grounded in what is now called the "iterative conception of set," makes for axiom (schemata) that are far simpler than those of conventional set theories, such as ZFC, with simpler ontologies. Set theories whose point of departure is type theory, but whose axioms, ontology, and terminology differ from the above, include New Foundations
and Scott–Potter set theory.
and Peter B. Andrews. Since ST is a higher order logic, and in higher order logics one can define propositional connectives in terms of logical equivalence
and quantifiers, in 1963 Henkin developed a formulation of ST based on equality, but in which he restricted attention to propositional types. This was simplified later that year by Andrews in his
theory Q0. In this respect ST can be seen as a particular kind of a higher-order logic, classified by P.T. Johnstone in Sketches of an Elephant, as having a lambda-signature, that is a higher-order signature
that contains no relations, and uses only products and arrows (function types) as type constructors. Furthermore, as Johnstone put it, ST is "logic-free" in the sense that it contains no logical connectives or quantifiers in its formulae.
feature that allows values of different data type
s to be handled using a uniform interface. The concept of parametric polymorphism applies to both data types and functions. A function that can evaluate to or be applied to values of different types is known as a polymorphic function. A data type that can appear to be of a generalized type (e.g., a list with elements of arbitrary type) is designated polymorphic data type like the generalized type from which such specializations are made.
that depends on a value. Dependent types play a central role in intuitionistic type theory
and in the design of functional programming languages like ATS
, Agda and Epigram.
An example is the type of n-tuples of real numbers. This is a dependent type because the type depends on the value n.
s for programming languages. Definitions of type system vary, but the following one due to Benjamin C. Pierce
roughly corresponds to the current consensus in the programming language theory community:
In other words, a type system divides program values into sets called types — this is called a type assignment — and makes certain program behaviors illegal on the basis of the types that are thus assigned. For example, a type system may classify the value "hello" as a string
and the value 5 as a number
, and prohibit the programmer from adding "hello" to 5 based on that type assignment. In this type system, the program
would be illegal. Hence, any program permitted by the type system would be provably free from the erroneous behavior of adding strings and numbers.
The design and implementation of type systems is a topic nearly as broad as the topic of programming languages itself. In fact, type theory proponents commonly proclaim that the design of type systems is the very essence of programming language design: "Design the type system correctly, and the language will design itself."
of natural language
s, especially Montague grammar
and its descendants. The most common construction takes the basic types
and 
for individuals and truth-values, respectively, and defines the set of types recursively as follows:
A complex type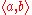
is the type of functions
from entities of type
to entities of type 
. Thus one has types like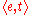 
which are interpreted as elements of the set of functions from entities to truth-values, i.e. characteristic function
s of sets of entities. An expression of type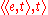
is a function from sets of entities to truth-values, i.e. a (characteristic function of a) set of sets. This latter type is standardly taken to be the type of natural language quantifiers
, like everybody or nobody (Montague 1973, Barwise and Cooper 1981).
introduced a theory of logical types into the social sciences; his notions of double bind
and logical levels
are based on Russell's theory of types.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, logic
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
and computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, type theory is any of several formal systems that can serve as alternatives to naive set theory
Naive set theory
Naive set theory is one of several theories of sets used in the discussion of the foundations of mathematics. The informal content of this naive set theory supports both the aspects of mathematical sets familiar in discrete mathematics , and the everyday usage of set theory concepts in most...
, or the study of such formalisms in general. In programming language theory
Programming language theory
Programming language theory is a branch of computer science that deals with the design, implementation, analysis, characterization, and classification of programming languages and their individual features. It falls within the discipline of computer science, both depending on and affecting...
, a branch of computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, type theory can refer to the design, analysis and study of type system
Type system
A type system associates a type with each computed value. By examining the flow of these values, a type system attempts to ensure or prove that no type errors can occur...
s, although some computer scientists limit the term's meaning to the study of abstract formalisms such as typed λ-calculi
Typed lambda calculus
A typed lambda calculus is a typed formalism that uses the lambda-symbol to denote anonymous function abstraction. In this context, types are usually objects of a syntactic nature that are assigned to lambda terms; the exact nature of a type depends on the calculus considered...
.
Bertrand Russell
Bertrand Russell
Bertrand Arthur William Russell, 3rd Earl Russell, OM, FRS was a British philosopher, logician, mathematician, historian, and social critic. At various points in his life he considered himself a liberal, a socialist, and a pacifist, but he also admitted that he had never been any of these things...
invented the first type theory in response to his discovery that Gottlob Frege
Gottlob Frege
Friedrich Ludwig Gottlob Frege was a German mathematician, logician and philosopher. He is considered to be one of the founders of modern logic, and made major contributions to the foundations of mathematics. He is generally considered to be the father of analytic philosophy, for his writings on...
's version of naive set theory
Naive set theory
Naive set theory is one of several theories of sets used in the discussion of the foundations of mathematics. The informal content of this naive set theory supports both the aspects of mathematical sets familiar in discrete mathematics , and the everyday usage of set theory concepts in most...
was afflicted with Russell's paradox
Russell's paradox
In the foundations of mathematics, Russell's paradox , discovered by Bertrand Russell in 1901, showed that the naive set theory created by Georg Cantor leads to a contradiction...
. This theory of types features prominently in Whitehead
Alfred North Whitehead
Alfred North Whitehead, OM FRS was an English mathematician who became a philosopher. He wrote on algebra, logic, foundations of mathematics, philosophy of science, physics, metaphysics, and education...
and Russell
Bertrand Russell
Bertrand Arthur William Russell, 3rd Earl Russell, OM, FRS was a British philosopher, logician, mathematician, historian, and social critic. At various points in his life he considered himself a liberal, a socialist, and a pacifist, but he also admitted that he had never been any of these things...
's Principia Mathematica
Principia Mathematica
The Principia Mathematica is a three-volume work on the foundations of mathematics, written by Alfred North Whitehead and Bertrand Russell and published in 1910, 1912, and 1913...
. It avoids Russell's paradox by first creating a hierarchy of types, then assigning each mathematical (and possibly other) entity to a type. Objects of a given type are built exclusively from objects of preceding types (those lower in the hierarchy), thus preventing loops.
Alonzo Church
Alonzo Church
Alonzo Church was an American mathematician and logician who made major contributions to mathematical logic and the foundations of theoretical computer science. He is best known for the lambda calculus, Church–Turing thesis, Frege–Church ontology, and the Church–Rosser theorem.-Life:Alonzo Church...
, inventor of the lambda calculus
Lambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
, developed a higher-order logic
Higher-order logic
In mathematics and logic, a higher-order logic is a form of predicate logic that is distinguished from first-order logic by additional quantifiers and a stronger semantics...
commonly called Church's Theory of Types, in order to avoid the Kleene–Rosser paradox afflicting the original pure lambda calculus. Church's type theory is a variant of the lambda calculus in which expressions (also called formulas or λ-terms) are classified into types, and the types of expressions restrict the ways in which they can be combined. In other words, it is a typed lambda calculus
Typed lambda calculus
A typed lambda calculus is a typed formalism that uses the lambda-symbol to denote anonymous function abstraction. In this context, types are usually objects of a syntactic nature that are assigned to lambda terms; the exact nature of a type depends on the calculus considered...
.
The article Church's Type Theory
in the Stanford Encyclopedia of Philosophy
is devoted to this subject.
Today many other such calculi are in use, including Per Martin-Löf
Per Martin-Löf
Per Erik Rutger Martin-Löf is a Swedish logician, philosopher, and mathematical statistician. He is internationally renowned for his work on the foundations of probability, statistics, mathematical logic, and computer science. Since the late 1970s, Martin-Löf's publications have been mainly in...
's Intuitionistic type theory
Intuitionistic type theory
Intuitionistic type theory, or constructive type theory, or Martin-Löf type theory or just Type Theory is a logical system and a set theory based on the principles of mathematical constructivism. Intuitionistic type theory was introduced by Per Martin-Löf, a Swedish mathematician and philosopher,...
, Jean-Yves Girard
Jean-Yves Girard
Jean-Yves Girard is a French logician working in proof theory. His contributions include a proof of strong normalization in a system of second-order logic called system F; the invention of linear logic; the geometry of interaction; and ludics...
's System F
System F
System F, also known as the polymorphic lambda calculus or the second-order lambda calculus, is a typed lambda calculus that differs from the simply typed lambda calculus by the introduction of a mechanism of universal quantification over types...
and the Calculus of Constructions
Calculus of constructions
The calculus of constructions is a formal language in which both computer programs and mathematical proofs can be expressed. This language forms the basis of theory behind the Coq proof assistant, which implements the derivative calculus of inductive constructions.-General traits:The CoC is a...
. In typed lambda calculi, types play a role similar to that of sets in set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
.
1900 - 1927
Origin of Russell's Theory of Types: In a letter to Gottlob FregeGottlob Frege
Friedrich Ludwig Gottlob Frege was a German mathematician, logician and philosopher. He is considered to be one of the founders of modern logic, and made major contributions to the foundations of mathematics. He is generally considered to be the father of analytic philosophy, for his writings on...
(1902) Russell announced his discovery of the paradox in Frege's Begriffsschrift
Begriffsschrift
Begriffsschrift is a book on logic by Gottlob Frege, published in 1879, and the formal system set out in that book...
. Frege promptly responded, acknowledging the problem and proposing a solution in a technical discussion of "levels". To quote Frege:
Incidentally, it seems to me that the expression "a predicate is predicated of itself" is not exact. A predicate is as a rule a first-level function, and this function requires an object as argument and cannot have itself as argument (subject). Therefore I would prefer to say "a concept is predicated of its own extension".
He goes about showing how this might work but seems to pull back from it. (In a footnote, van Heijenoort notes that in Frege 1893 Frege had used a symbol (horseshoe) "for reducing second-level functions to first-level functions"). As a consequence of what has become known as Russell's paradox
Russell's paradox
In the foundations of mathematics, Russell's paradox , discovered by Bertrand Russell in 1901, showed that the naive set theory created by Georg Cantor leads to a contradiction...
both Frege and Russell had to quickly emend works that they had at the printers. In an Appendix B that Russell tacked on to his 1903 Principles of Mathematics one finds his "tentative" "theory of types".
The matter plagued Russell for about five years (1903–1908). Willard Quine in his preface to Russell's (1908a) Mathematical logic as based on the theory of types presents a historical synopsis of the origin of the theory of types and the "ramified" theory of types: Russell proposed in turn a number of alternatives: (i) abandoning the theory of types (1905) followed by three theories in 1905: (ii.1) the zigzag theory, (ii.2) theory of limitation of size, (ii.3) the no-class theory (1905–1906), then (iii) readopting the theory of types (1908ff)".
Quine observes that Russell's introduction of the notion of "apparent variable" had the following result: "the distinction between 'all' and 'any': 'all' is expressed by the bound ('apparent') variable of universal quantification, which ranges over a type, and 'any' is expressed by the free ('real') variable which refers schematically to any unspecified thing irrespective of type". Quine dismisses this notion of "bound variable" as "pointless apart from a certain aspect of the theory of types".
The 1908 "ramified" theory of types
Quine explains the ramified theory as follows: "It has been so called because the type of a function depends both on the types of its arguments and on the types of the apparent variables contained in it (or in its expresion), in case these exceed the types of the arguments". Stephen Kleene in his 1952 Introduction to Metamathematics describes the ramified theory of types this way:- The primary objects or individuals (i.e. the given things not being subjected to logical analysis) are assigned to one type (say type 0), the properties of individuals to type 1, properties of properties of individuals to type 2, etc.; and no properties are admitted which do not fall into one of these logical types (e.g. this puts the properties 'predicable' and 'impredicable' ... outside the pale of logic). A more detailed account would describe the admitted types for other objects as relations and classes. Then to exclude impredicative definitions within a type, the types above type 0 are further separated into orders. Thus for type 1, properties defined without mentioning any totality belong to order 0, and properties defined using the totality of properties of a given order belong to the next higher order. ... But this separation into orders makes it impossible to construct the familiar analysis, which we saw above contains impredicative definitions. To escape this outcome, Russell postulated his axiom of reducibilityAxiom of reducibilityThe axiom of reducibility was introduced by Bertrand Russell as part of his ramified theory of types, an attempt to ground mathematics in first-order logic.- History: the problem of impredicativity :...
, which asserts that to any property belonging to an order above the lowest, there is a coextensive property (i.e. one possessed by exactly the same objects) of order 0. If only definable properties are considered to exist, then the axiom means that to every impredicative definition within a given type there is an equivalent predicative one (Kleene 1952:44-45).
The axiom of reducibility and the notion of "matrix"
But because the stipulations of the ramified theory would prove (to quote Quine) "onerous", Russell in his 1908 Mathematical logic as based on the theory of types also would propose his axiom of reducibilityAxiom of reducibility
The axiom of reducibility was introduced by Bertrand Russell as part of his ramified theory of types, an attempt to ground mathematics in first-order logic.- History: the problem of impredicativity :...
. By 1910 Whitehead and Russell in their Principia Mathematica would further augment this axiom with the notion of a matrix -- a fully extensional specification of a function. From its matrix a function could be derived by the process of "generalization" and vice versa, i.e. the two processes are reversible -- (i) generalization from a matrix to a function ( by use apparent variables ) and (ii) the reverse process of reduction of type by courses-of-values substitution of arguments for the apparent variable. By this method impredicativity could be avoided.
Truth tables
Eventually Emil Post (1921) would lay waste to Russell's "cumbersome" Theory of Types with his "truth functions" and their truth tables. In his "Introduction" to his 1921 Post places the blame on Russell's notion of apparent variable: "Whereas the complete theory [of Whitehead and Russell (1910, 1912, 1913)] requires for the enunciation of its propositions real and apparent variables, which represent both individuals and propositional functionPropositional function
A propositional function in logic, is a statement expressed in a way that would assume the value of true or false, except that within the statement is a variable that is not defined or specified, which leaves the statement undetermined...
s of different kinds, and as a result necessitates the cumbersome theory of types, this subtheory uses only real variables, and these real variables represent but one kind of entity, which the authors have chosen to call elementary propositions".
At about the same time Ludwig Wittgenstein
Ludwig Wittgenstein
Ludwig Josef Johann Wittgenstein was an Austrian philosopher who worked primarily in logic, the philosophy of mathematics, the philosophy of mind, and the philosophy of language. He was professor in philosophy at the University of Cambridge from 1939 until 1947...
made short work of the theory of types in his 1922 work Tractatus Logico-Philosophicus
Tractatus Logico-Philosophicus
The Tractatus Logico-Philosophicus is the only book-length philosophical work published by the Austrian philosopher Ludwig Wittgenstein in his lifetime. It was an ambitious project: to identify the relationship between language and reality and to define the limits of science...
in which he points out the following in parts 3.331–3.333:
Wittgenstein proposed the truth-table method as well. In his 4.3 through 5.101, Wittgenstein adopts an unbounded Sheffer stroke
Sheffer stroke
In Boolean functions and propositional calculus, the Sheffer stroke, named after Henry M. Sheffer, written "|" , "Dpq", or "↑", denotes a logical operation that is equivalent to the negation of the conjunction operation, expressed in ordinary language as "not both"...
as his fundamental logical entity and then lists all 16 functions of two variables (5.101).
The notion of matrix-as-truth-table appears as late as the 1940-1950's in the work of Tarski, e.g. his 1946 indexes "Matrix, see: Truth table"
Russell's doubts
Russell in his 1920 Introduction to Mathematical Philosophy devotes an entire chapter to "The axiom of Infinity and logical types" wherein he states his concerns: "Now the theory of types emphatically does not belong to the finished and certain part of our subject: much of this theory is still inchoate, confused, and obscure. But the need of some doctrine of types is less doubtful than the precise form the doctrine should take; and in connection with the axiom of infinity it is particularly easy to see the necessity of some such doctrine".Russell abandons the axiom of reducibility: In the second edition of Principia Mathematica (1927) he acknowledges Wittgenstein's argument. At the outset of his Introduction he declares "there can be no doubt ... that there is no need of the distinction between real and apparent variables...". Now he fully embraces the matrix notion and declares "A function can only appear in a matrix through its values" (but demurs in a footnote: "It takes the place (not quite adequately) of the axiom of reducibility"). Furthermore, he introduces a new (abbreviated, generalized) notion of "matrix", that of a "logical matrix . . . one that contains no constants. Thus p|q is a logical matrix". Thus Russell has virtually abandoned the axiom of reducibility, but in his last paragraphs he states that from "our present primitive propositions" he cannot derive "Dedekindian relations and well-ordered relations" and observes that if there is a new axiom to replace the axiom of reducibility "it remains to be discovered".
Theory of simple types
In the 1920s, Leon ChwistekLeon Chwistek
Leon Chwistek was a Polish avant-garde painter, theoretician of modern art, literary critic, logician, philosopher and mathematician.-Logic and philosophy:...
and Frank P. Ramsey
Frank P. Ramsey
Frank Plumpton Ramsey was a British mathematician who, in addition to mathematics, made significant and precocious contributions in philosophy and economics before his death at the age of 26...
noticed that, if one is willing to give up the vicious circle principle
Vicious circle principle
The vicious circle principle is a principle that was endorsed by many predicativist mathematicians in the early 20th century to prevent contradictions. The principle states that no object or property may be introduced by a definition that depends on that object or property itself...
,
the hierarchy of levels of types in the "ramified theory of types" (see the History section for more on this) can be collapsed.
The resulting restricted logic is called the theory of simple types or, perhaps more commonly, simple type theory. Detailed formulations of simple type theory were published in the late 1920s and early 1930s
by R. Carnap, F. Ramsey, W.V.O. Quine, and A. Tarski. In 1940 Alonzo Church
Alonzo Church
Alonzo Church was an American mathematician and logician who made major contributions to mathematical logic and the foundations of theoretical computer science. He is best known for the lambda calculus, Church–Turing thesis, Frege–Church ontology, and the Church–Rosser theorem.-Life:Alonzo Church...
(re)formulated it as simply typed lambda calculus
Simply typed lambda calculus
The simply typed lambda calculus , a formof type theory, is a typed interpretation of the lambda calculus with only one type constructor: \to that builds function types. It is the canonical and simplest example of a typed lambda calculus...
. and examined by Gödel in his 1944.
Gödel 1944
Kurt GödelKurt Gödel
Kurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
in his 1944 Russell's mathematical logic gave the following definition of the "theory of simple types" in a footnote:
- By the theory of simple types I mean the doctrine which says that the objects of thought (or, in another interpretation, the symbolic expressions) are divided into types, namely: individuals, properties of individuals, relations between individuals, properties of such relations, etc. (with a similar hierarchy for extensions), and that sentences of the form: " a has the property φ ", " b bears the relation R to c ", etc. are meaningless, if a, b, c, R, φ are not of types fitting together. Mixed types (such as classes containing individuals and classes as elements) and therefore also transfinite types (such as the class of all classes of finite types) are excluded. That the theory of simple types suffices for avoiding also the epistemological paradoxes is shown by a closer analysis of these. (Cf. Ramsey 1926 and Tarski 1935, p. 399).".
He concluded the (1) theory of simple types and (2) axiomatic set theory, "permit the derivation of modern mathematics and at the same time avoid all known paradoxes" (Gödel 1944:126); furthermore, the theory of simple types "is the system of the first Prinicipa [Principia Mathematica] in an appropriate interpretation. . . . [However}, many symptoms show only too clearly, however, that the primitive concepts need further elucidation" (Gödel 1944:126).
Mendelson's ST
The following system is Mendelson's (1997, 289–293) ST.ST is equivalent with Russell's ramified theory plus the Axiom of reducibility
Axiom of reducibility
The axiom of reducibility was introduced by Bertrand Russell as part of his ramified theory of types, an attempt to ground mathematics in first-order logic.- History: the problem of impredicativity :...
.
The domain of quantification
Domain of discourse
In the formal sciences, the domain of discourse, also called the universe of discourse , is the set of entities over which certain variables of interest in some formal treatment may range...
is partitioned into an ascending hierarchy of types, with all individual
Individual
An individual is a person or any specific object or thing in a collection. Individuality is the state or quality of being an individual; a person separate from other persons and possessing his or her own needs, goals, and desires. Being self expressive...
s assigned a type. Quantified variables range over only one type; hence the underlying logic is first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
. ST is "simple" (relative to the type theory of Principia Mathematica
Principia Mathematica
The Principia Mathematica is a three-volume work on the foundations of mathematics, written by Alfred North Whitehead and Bertrand Russell and published in 1910, 1912, and 1913...
) primarily because all members of the domain
Relation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
and codomain
Relation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
of any relation
Relation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
must be of the same type.
There is a lowest type, whose individuals have no members and are members of the second lowest type. Individuals of the lowest type correspond to the urelements of certain set theories. Each type has a next higher type, analogous to the notion of successor in Peano arithmetic. While ST is silent as to whether there is a maximal type, a transfinite number of types poses no difficulty. These facts, reminiscent of the Peano axioms, make it convenient and conventional to assign a natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
to each type, starting with 0 for the lowest type. But type theory does not require a prior definition of the naturals.
The symbols peculiar to ST are primed variables and infix
. In any given formula, unprimed variables all have the same type, while primed variables (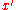) range over the next higher type. The atomic formulaAtomic formula
In mathematical logic, an atomic formula is a formula with no deeper propositional structure, that is, a formula that contains no logical connectives or equivalently a formula that has no strict subformulas. Atoms are thus the simplest well-formed formulas of the logic...
s of ST are of two forms,
(identityIdentity (mathematics)
In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...
) and
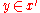. The infixInfix
An infix is an affix inserted inside a word stem . It contrasts with adfix, a rare term for an affix attached to the end of a stem, such as a prefix or suffix.-Indonesian:...
symbol
suggests the intended interpretationModel theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, set membership.
All variables appearing in the definition of identity and in the axioms Extensionality and Comprehension, range over individuals of one of two consecutive types. Only unprimed variables (ranging over the "lower" type) can appear to the left of '
', where as to its right, only primed variables (ranging over the "higher" type) can appear. The first-order formulation of ST rules out quantifying over types. Hence each pair of consecutive types requires its own axiom of Extensionality and of Comprehension, which is possible if Extensionality and Comprehension below are taken as axiom schemata "ranging over" types.- Identity, defined by
.
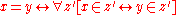- ExtensionalityAxiom of extensionalityIn axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of extensionality, or axiom of extension, is one of the axioms of Zermelo-Fraenkel set theory.- Formal statement :...
. An axiom schemaAxiom schemaIn mathematical logic, an axiom schema generalizes the notion of axiom.An axiom schema is a formula in the language of an axiomatic system, in which one or more schematic variables appear. These variables, which are metalinguistic constructs, stand for any term or subformula of the system, which...
.
.
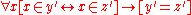- Let
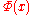denote any first-order formulaFirst-order logicFirst-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
containing the free variable
.
- Comprehension. An axiom schemaAxiom schemaIn mathematical logic, an axiom schema generalizes the notion of axiom.An axiom schema is a formula in the language of an axiomatic system, in which one or more schematic variables appear. These variables, which are metalinguistic constructs, stand for any term or subformula of the system, which...
.
.
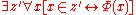- Remark. Any collection of elements of the same type may form an object of the next higher type. Comprehension is schematic with respect to
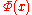as well as to types.
- InfinityAxiom of infinityIn axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of infinity is one of the axioms of Zermelo-Fraenkel set theory...
. There exists a nonempty binary relationBinary relationIn mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
over the individuals of the lowest type, that is irreflexiveReflexive relationIn mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
, transitiveTransitive relationIn mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
, and strongly connected: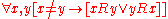
.
- Remark. Infinity is the only true axiom of ST and is entirely mathematical in nature. It asserts that
is a strict total orderTotal orderIn set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
, with a domainRelation (mathematics)In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
identical to its codomainRelation (mathematics)In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
. If 0 is assigned to the lowest type, the type of
is 3. Infinity can be satisfied only if the (co)domain of 
is infinite, thus forcing the existence of an infinite set. If relations are defined in terms of ordered pairOrdered pairIn mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
s, this axiom requires a prior definition of ordered pair; the Kuratowski definition, adapted to ST, will do. The literature does not explain why the usual axiom of infinityAxiom of infinityIn axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of infinity is one of the axioms of Zermelo-Fraenkel set theory...
(there exists an inductive setInductive set (axiom of infinity)In the context of the axiom of infinity, an inductive set is a set X with the property that, for every x \in X, the successor x' of x is also an element of X and the set X contains the empty set \varnothing....
) of ZFC of other set theories could not be married to ST.
ST reveals how type theory can be made very similar to axiomatic set theory. Moreover, the more elaborate ontology of ST, grounded in what is now called the "iterative conception of set," makes for axiom (schemata) that are far simpler than those of conventional set theories, such as ZFC, with simpler ontologies. Set theories whose point of departure is type theory, but whose axioms, ontology, and terminology differ from the above, include New Foundations
New Foundations
In mathematical logic, New Foundations is an axiomatic set theory, conceived by Willard Van Orman Quine as a simplification of the theory of types of Principia Mathematica. Quine first proposed NF in a 1937 article titled "New Foundations for Mathematical Logic"; hence the name...
and Scott–Potter set theory.
Formulations based on equality
Church’s type theory has been extensively studied by two of Church’s students, Leon HenkinLeon Henkin
Leon Albert Henkin was a logician at the University of California, Berkeley. He was principally known for the "Henkin's completeness proof": his version of the proof of the semantic completeness of standard systems of first-order logic.-The completeness proof:Henkin's result was not novel; it had...
and Peter B. Andrews. Since ST is a higher order logic, and in higher order logics one can define propositional connectives in terms of logical equivalence
Logical equivalence
In logic, statements p and q are logically equivalent if they have the same logical content.Syntactically, p and q are equivalent if each can be proved from the other...
and quantifiers, in 1963 Henkin developed a formulation of ST based on equality, but in which he restricted attention to propositional types. This was simplified later that year by Andrews in his
theory Q0. In this respect ST can be seen as a particular kind of a higher-order logic, classified by P.T. Johnstone in Sketches of an Elephant, as having a lambda-signature, that is a higher-order signature
Signature (logic)
In logic, especially mathematical logic, a signature lists and describes the non-logical symbols of a formal language. In universal algebra, a signature lists the operations that characterize an algebraic structure. In model theory, signatures are used for both purposes.Signatures play the same...
that contains no relations, and uses only products and arrows (function types) as type constructors. Furthermore, as Johnstone put it, ST is "logic-free" in the sense that it contains no logical connectives or quantifiers in its formulae.
Type polymorphism
Polymorphism is a programming languageProgramming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
feature that allows values of different data type
Data type
In computer programming, a data type is a classification identifying one of various types of data, such as floating-point, integer, or Boolean, that determines the possible values for that type; the operations that can be done on values of that type; the meaning of the data; and the way values of...
s to be handled using a uniform interface. The concept of parametric polymorphism applies to both data types and functions. A function that can evaluate to or be applied to values of different types is known as a polymorphic function. A data type that can appear to be of a generalized type (e.g., a list with elements of arbitrary type) is designated polymorphic data type like the generalized type from which such specializations are made.
Dependent types
Dependent type is a typeType system
A type system associates a type with each computed value. By examining the flow of these values, a type system attempts to ensure or prove that no type errors can occur...
that depends on a value. Dependent types play a central role in intuitionistic type theory
Intuitionistic type theory
Intuitionistic type theory, or constructive type theory, or Martin-Löf type theory or just Type Theory is a logical system and a set theory based on the principles of mathematical constructivism. Intuitionistic type theory was introduced by Per Martin-Löf, a Swedish mathematician and philosopher,...
and in the design of functional programming languages like ATS
ATS (programming language)
ATS is a programming language whose stated purpose is to support theorem proving in combination with practical programming through the use of advanced type systems. The performance of ATS has been demonstrated to be comparable to that of the C and C++ programming languages...
, Agda and Epigram.
An example is the type of n-tuples of real numbers. This is a dependent type because the type depends on the value n.
Computing
The most obvious application of type theory is in constructing type checking algorithms in the semantic analysis phase of compilerCompiler
A compiler is a computer program that transforms source code written in a programming language into another computer language...
s for programming languages. Definitions of type system vary, but the following one due to Benjamin C. Pierce
Benjamin C. Pierce
Benjamin Crawford Pierce is an American professor of computer science at the University of Pennsylvania. Pierce joined Penn in 1998 from Indiana University and held research positions at the University of Cambridge and the University of Edinburgh. He received his Ph.D. from Carnegie Mellon...
roughly corresponds to the current consensus in the programming language theory community:
In other words, a type system divides program values into sets called types — this is called a type assignment — and makes certain program behaviors illegal on the basis of the types that are thus assigned. For example, a type system may classify the value "hello" as a string
String (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
and the value 5 as a number
Number
A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....
, and prohibit the programmer from adding "hello" to 5 based on that type assignment. In this type system, the program
would be illegal. Hence, any program permitted by the type system would be provably free from the erroneous behavior of adding strings and numbers.
The design and implementation of type systems is a topic nearly as broad as the topic of programming languages itself. In fact, type theory proponents commonly proclaim that the design of type systems is the very essence of programming language design: "Design the type system correctly, and the language will design itself."
Linguistics
Type theory is also widely in use in formal theories of semanticsFormal semantics (linguistics)
In linguistics, formal semantics seeks to understand linguistic meaning by constructing precise mathematical models of the principles that speakers use to define relations between expressions in a natural language and the world which supports meaningful discourse.The mathematical tools used are the...
of natural language
Natural language
In the philosophy of language, a natural language is any language which arises in an unpremeditated fashion as the result of the innate facility for language possessed by the human intellect. A natural language is typically used for communication, and may be spoken, signed, or written...
s, especially Montague grammar
Montague grammar
Montague grammar is an approach to natural language semantics, named after American logician Richard Montague. The Montague grammar is based on formal logic, especially higher order predicate logic and lambda calculus, and makes use of the notions of intensional logic, via Kripke models...
and its descendants. The most common construction takes the basic types
and for individuals and truth-values, respectively, and defines the set of types recursively as follows:- if
and 
are types, then so is 
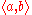. - Nothing except the basic types, and what can be constructed from them by means of the previous clause are types.
A complex type
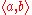is the type of functionsFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
from entities of type
to entities of type . Thus one has types like 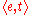which are interpreted as elements of the set of functions from entities to truth-values, i.e. characteristic functionCharacteristic function
In mathematics, characteristic function can refer to any of several distinct concepts:* The most common and universal usage is as a synonym for indicator function, that is the function* In probability theory, the characteristic function of any probability distribution on the real line is given by...
s of sets of entities. An expression of type
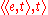is a function from sets of entities to truth-values, i.e. a (characteristic function of a) set of sets. This latter type is standardly taken to be the type of natural language quantifiersGeneralized quantifier
In linguistic semantics, a generalized quantifier is an expression that denotes a property of a property, also called a higher-order property. This is the standard semantics assigned to quantified noun phrases, also called determiner phrases, in short: DP...
, like everybody or nobody (Montague 1973, Barwise and Cooper 1981).
Social sciences
Gregory BatesonGregory Bateson
Gregory Bateson was an English anthropologist, social scientist, linguist, visual anthropologist, semiotician and cyberneticist whose work intersected that of many other fields. He had a natural ability to recognize order and pattern in the universe...
introduced a theory of logical types into the social sciences; his notions of double bind
Double bind
A double bind is an emotionally distressing dilemma in communication in which an individual receives two or more conflicting messages, in which one message negates the other. This creates a situation in which a successful response to one message results in a failed response to the other , so that...
and logical levels
Neurology
Neurology is a medical specialty dealing with disorders of the nervous system. Specifically, it deals with the diagnosis and treatment of all categories of disease involving the central, peripheral, and autonomic nervous systems, including their coverings, blood vessels, and all effector tissue,...
are based on Russell's theory of types.
Connections to constructive logic
See also
- Category theoryCategory theoryCategory theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
- Data typeData typeIn computer programming, a data type is a classification identifying one of various types of data, such as floating-point, integer, or Boolean, that determines the possible values for that type; the operations that can be done on values of that type; the meaning of the data; and the way values of...
for concrete types of data in programming - Domain theoryDomain theoryDomain theory is a branch of mathematics that studies special kinds of partially ordered sets commonly called domains. Consequently, domain theory can be considered as a branch of order theory. The field has major applications in computer science, where it is used to specify denotational...
- Type systemType systemA type system associates a type with each computed value. By examining the flow of these values, a type system attempts to ensure or prove that no type errors can occur...
for a more practical discussion of type systems for programming languages - Type (model theory)
Further reading
- Constable, Robert L.Robert Lee ConstableRobert "Bob" Lee Constable is a professor of computer science and first and former dean of the department at Cornell University. He is known for his work on connecting computer programs and mathematical proofs, especially the NuPRL system. Constable received his PhD in 1968 under Stephen Kleene and...
, 2002, "Naïve Computational Type Theory," in H. Schwichtenberg and R. Steinbruggen (eds.), Proof and System-Reliability: 213–259. Intended as an type theory counterpart of Paul HalmosPaul HalmosPaul Richard Halmos was a Hungarian-born American mathematician who made fundamental advances in the areas of probability theory, statistics, operator theory, ergodic theory, and functional analysis . He was also recognized as a great mathematical expositor.-Career:Halmos obtained his B.A...
's (1960) Naïve Set TheoryNaive Set Theory (book)Naive Set Theory is a mathematics textbook by Paul Halmos originally published in 1960. This book is an undergraduate introduction to not-very-naive set theory. It is still considered by many to be the best introduction to set theory for beginners...
Covers type theory in depth, including polymorphic and dependent type extensions. Gives categorical semantics. - Cardelli, Luca, 1997, "Type Systems," in Allen B. Tucker, ed., The Computer Science and Engineering Handbook. CRC Press: 2208–2236.
- Thompson, Simon, 1991. Type Theory and Functional Programming. Addison-Wesley. ISBN 0-201-41667-0.
- J. Roger HindleyJ. Roger HindleyJ. Roger Hindley is a prominent British logician best known for the Hindley–Milner type inference algorithm. Since 1998, he has been an Honorary Research Fellow at Swansea University.-Education:...
, Basic Simple Type Theory, Cambridge University Press, 2008, ISBN 0521054222 (also 1995, 1997). A good introduction to simple type theory for computer scientists; the system described is not exactly Church's STT though. Book review - Stanford Encyclopedia of PhilosophyStanford Encyclopedia of PhilosophyThe Stanford Encyclopedia of Philosophy is a freely-accessible online encyclopedia of philosophy maintained by Stanford University. Each entry is written and maintained by an expert in the field, including professors from over 65 academic institutions worldwide...
: Type Theory" – by Thierry CoquandThierry CoquandThierry Coquand is a professor in computer science at the University of Gothenburg, Sweden. He is known for his work in constructive mathematics, especially the calculus of constructions. He received his Ph.D. under the supervision of Gérard Huet.- External links :*...
. - Fairouz D. Kamareddine, Twan Laan, Rob P. Nederpelt, A modern perspective on type theory: from its origins until today, Springer, 2004, ISBN 1402023340
- José Ferreirós, José Ferreirós Domínguez, Labyrinth of thought: a history of set theory and its role in modern mathematics, Edition 2, Springer, 2007, ISBN 3764383496, chapter X "Logic and Type Theory in the Interwar Period"
Sources for History section
- Bertrand Russell (1903) The Principles of Mathematics: Vol. 1, Cambridge at the University Press, Cambridge, UK, republished as a googlebook.
- Bertrand Russell (1920) Introduction to Mathematical Philosophy (second edition), Dover Publishing Inc., New York NY, ISBN 0-486-27724-0 (pbk).
- Alfred Tarski (1946) Introduction to Logic and to the Methodology of Deductive Sciences, republished 1995 by Dover Publications, Inc., New York, NY ISBN 0-486-28462-x
- Jean van Heijenoort (1967, 3rd printing 1976), From Frege to Godel: A Source Book in Mathematical Logic, 1879-1931, Harvard University Press, Cambridge, MA, ISBN 0-674-32449-8 (pbk)
- Bertrand Russell (1902) Letter to Frege with commentary by van Heijenoort, pages 124-125. Wherein Russell announces his discovery of a "paradox" in Frege's work.
- Gottlob Frege (1902) Letter to Russell with commentary by van Heijenoort, pages 126-128.
- Bertrand Russell (1908a) Mathematical logic as based on the theory of types, with commentary by Willard Quine, pages 150-182.
- Emil Post (1921) Introduction to a general theory of elementary propositions, with commentary by van Heijenoort, pages 264-283.
- Alfred North Whitehead and Bertrand Russell(1910–1913, 1927 2nd edition reprinted 1962), Principia Mathematica to *56, Cambridge at the University Press, London UK, no ISBN or US card catalog number.
- Ludwig Wittgenstein (republished 2009) Major Works: Selected Philosophical Writings", HarperCollins, New York. ISBN 978-0-06-155024-9. Wittgenstein's (1921 in English) Tractatus Logico-Philosophicus pages 1–82.
External links
- Types Project lecture notes of summer schools 2005-2008
- The 2005 summer school has introductory lectures
- [ftp://ftp.cs.cornell.edu/pub/nuprl/doc/book.ps.gz The Nuprl Book]: "Introduction to Type Theory."