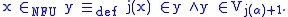New Foundations
Encyclopedia
In mathematical logic
, New Foundations (NF) is an axiomatic set theory, conceived by Willard Van Orman Quine
as a simplification of the theory of types of Principia Mathematica
. Quine first proposed NF in a 1937 article titled "New Foundations for Mathematical Logic"; hence the name. Much of this entry discusses NFU, an important variant of NF due to Jensen (1969) and exposited in Holmes (1998).
, are equality (
) and membership (
). TST has a linear hierarchy of types: type 0 consists of individuals otherwise undescribed. For each (meta-) natural number n, type n+1 objects are sets of type n objects; sets of type n have members of type n-1. Objects connected by identity must have the same type. The following two atomic formulas succinctly describe the typing rules: 
and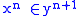 
(notation to be improved).
The axioms of TST are:
This type theory is much less complicated than the one first set out in the Principia Mathematica
, which included types for relations
whose arguments were not necessarily all of the same type. In 1914, Norbert Wiener
showed how to code the ordered pair
as a set of sets, making it possible to eliminate relation types in favor of the linear hierarchy of sets described here.
By convention, NF's Comprehension schema is stated using the concept of stratified formula and making no direct reference to types. A formula
is said to be stratified if there exists a function
f from pieces of syntax to the natural numbers, such that for any atomic subformula
of 
we have f(y) = f(x) + 1, while for any atomic subformula 
of 
, we have f(x) = f(y). Comprehension then becomes: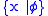
exists for each stratified formula 
.
Even the indirect reference to types implicit in the notion of stratification
can be eliminated. Theodore Hailperin showed in 1944 that Comprehension is equivalent to a finite conjunction of its instances, so that NF can be finitely axiomatized without any reference to the notion of type.
Comprehension may seem to run afoul of problems similar to those in naive set theory
, but this is not the case. For example, the impossible Russell class
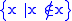is not an NF set, because 
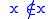cannot be stratified.
and functions
are defined in TST (and in NF and NFU) as sets of ordered pair
s in the usual way. The usual definition of the ordered pair, first proposed by Kuratowski in 1921, has a serious drawback for NF and related theories: the resulting ordered pair necessarily has a type two higher than the type of its arguments (its left and right projection
s). Hence for purposes of determining stratification, a function is three types higher than the members of its field.
If one can define a pair in such a way that its type is the same type as that of its arguments (resulting in a type-level ordered pair), then a relation or function is merely one type higher than the type of the members of its field. Hence NF and related theories usually employ Quine
's set-theoretic definition of the ordered pair, which yields a type-level ordered pair. Holmes (1998) takes the ordered pair and its left and right projection
s as primitive. Fortunately, whether the ordered pair is type-level by definition or by assumption (i.e., taken as primitive) usually does not matter.
The existence of a type-level ordered pair implies Infinity, and NFU + Infinity interprets NFU + "there is a type level ordered pair" (they are not quite the same theory, but the differences are inessential). Conversely, NFU + Infinity + Choice proves the existence of a type-level ordered pair.
; this is a highly desirable property for any set theory to have. Intuitively, it means that the functions of NF do not curry
as one would normally expect functions to. Furthermore, it means that NF is not a topos
.
to any mainstream mathematical system. NF disproves Choice, and so proves Infinity (Specker, 1953). But it is also known (Jensen
, 1969) that the minor(?) modification of allowing urelements (objects lacking members which are distinct from the empty set and from one another) yields NFU, a theory that is consistent relative to Peano arithmetic; if Infinity and Choice are added, the resulting theory has the same consistency strength as type theory with infinity or bounded Zermelo set theory. (NFU corresponds to a type theory TSTU, where positive types may contain urelements.) There are other relatively consistent variants of NF.
NFU is, roughly speaking, weaker than NF because in NF, the power set of the universe is the universe itself, while in NFU, the power set of the universe may be strictly smaller than the universe (the power set of the universe contains only sets, while the universe may contain urelements). In fact, this is necessarily the case in NFU+"Choice".
Specker has shown that NF is equiconsistent
with TST + Amb, where Amb is the axiom scheme of typical ambiguity which asserts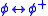
for any formula 
, 
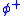being the formula obtained by raising every type index in 
by one. NF is also equiconsistent with the theory TST augmented with a "type shifting automorphism", an operation which raises type by one, mapping each type onto the next higher type, and preserves equality and membership relations (and which cannot be used in instances of Comprehension: it is external to the theory). The same results hold for various fragments of TST in relation to the corresponding fragments of NF.
In the same year (1969) that Jensen
proved NFU consistent, Grishin proved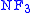
consistent. 
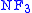is the fragment of NF with full extensionality (no urelements) and those instances of Comprehension which can be stratified using just three types. This theory is a very awkward medium for mathematics (although there have been attempts to alleviate this awkwardness), largely because there is no obvious definition for an ordered pair
. Despite this awkwardness,
is very interesting because every infinite model of TST restricted to three types satisfies Amb. Hence for every such model there is a model of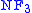 
with the same theory. This does not hold for four types: 
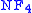is the same theory as NF, and we have no idea how to obtain a model of TST with four types in which Amb holds.
In 1983, Marcel Crabbé proved consistent a system he called NFI, whose axioms are unrestricted extensionality and those instances of Comprehension in which no variable is assigned a type higher than that of the set asserted to exist. This is a predicativity
restriction, though NFI is not a predicative theory: it admits enough impredicativity to define the set of natural numbers (defined as the intersection of all inductive sets; note that the inductive sets quantified over are of the same type as the set of natural numbers being defined). Crabbé also discussed a subtheory of NFI, in which only parameters (free variables) are allowed to have the type of the set asserted to exist by an instance of Comprehension. He called the result "predicative NF" (NFP); it is, of course, doubtful whether any theory with a self-membered universe is truly predicative. Holmes has shown that NFP has the same consistency strength as the predicative theory of types of Principia Mathematica
without the Axiom of Reducibility
.
es of set theory
. That NFU, a {relatively} consistent theory, also avoids the paradoxes increases our confidence in this fact.
The Russell paradox: An easy matter;
is not a stratified formula, so the existence of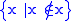 
is not asserted by any instance of Comprehension. Quine presumably constructed NF with this paradox uppermost in mind.
Cantor's paradox
of the largest cardinal number
exploits the application of Cantor's theorem
to the universal set
. Cantor's theorem
says (given ZFC) that the power set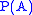
of any set 
is larger than 
(there can be no injection
(one-to-one map) from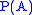
into 
). Now of course there is an injection
from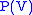
into 
, if 
is the universal set! The resolution requires that we observe that 
makes no sense in the theory of types: the type of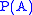 
is one higher than the type of 
. The correctly typed version (which is a theorem in the theory of types for essentially the same reasons that the original form of Cantor's theorem
works in ZF
) is
, where 
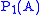is the set of one-element subsets of 
. The specific instance of this theorem that interests us is 
: there are fewer one-element sets than sets (and so fewer one-element sets than general objects, if we are in NFU). The "obvious" bijection
from the universe to the one-element sets is not a set; it is not a set because its definition is unstratified. Note that in all known models of NFU it is the case that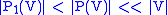 
; Choice allows one not only to prove that there are urelements but that there are many cardinals between 
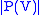and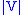 
.
We now introduce some useful notions. A set
which satisfies the intuitively appealing 
is said to be cantorian: a cantorian set satisfies the usual form of Cantor's theorem
. A set
which satisfies the further condition that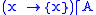 
, the restriction
of the singleton map to A, is not only cantorian set but strongly cantorian.
The Burali-Forti paradox
of the largest ordinal number
goes as follows. We define (following naive set theory
) the ordinals as equivalence classes of well-orderings under similarity
. There is an obvious natural well-ordering on the ordinals; since it is a well-ordering it belongs to an ordinal
. It is straightforward to prove (by transfinite induction
) that the order type of the natural order on the ordinals less than a given ordinal
is 
itself. But this means that 
is the order type of the ordinals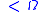 
and so is strictly less than the order type of all the ordinals — but the latter is, by definition, 
itself!
The solution to the paradox in NF(U) starts with the observation that the order type of the natural order on the ordinals less than
is of a higher type than 
. Hence a type level ordered pair
is two, and the usual Kuratowski ordered pair, four, types higher than the type of its arguments. For any order type
, we can define an order type 
one type higher: if 
, then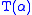 
is the order type of the order 
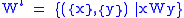. The triviality of the T operation is only a seeming one; it is easy to show that T is a strictly monotone
(order preserving) operation on the ordinals.
We can now restate the lemma on order types in a stratified manner: the order type of the natural order on the ordinals
is 
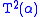or 
depending on which pair is used (we assume the type level pair hereinafter). From this we deduce that the order type on the ordinals
is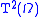 
, from which we deduce 
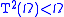. Hence the T operation is not a function; we cannot have a strictly monotone
set map from ordinals to ordinals which sends an ordinal downward! Since T is monotone, we have
, a "descending sequence" in the ordinals which cannot be a set.
Some have asserted that this result shows that no model of NF(U) is "standard", since the ordinals in any model of NFU are externally not well-ordered. We do not take a position on this, but we note that it is also a theorem of NFU that any set model of NFU has non-well-ordered "ordinals"; NFU does not conclude that the universe V is a model of NFU, despite V being a set, because the membership relation is not a set relation.
For a further development of mathematics in NFU
, with a comparison to the development of the same in ZFC, see implementation of mathematics in set theory
.
The set theory of the 1940 first edition of Quine
's Mathematical Logic married NF to the proper classes of NBG set theory, and included an axiom schema of unrestricted comprehension for proper classes. In 1942, J. Barkley Rosser proved that the system presented in Mathematical Logic was subject to the Burali-Forti paradox. This result does not apply to NF. In 1950, Hao Wang showed how to amend Quine's axioms so as to avoid this problem, and Quine included the resulting axiomatization in the 1951 second and final edition of Mathematical Logic.
, one can construct a nonstandard model of Zermelo set theory
(nothing nearly as strong as full ZFC is needed for the basic technique) on which there is an external automorphism j (not a set of the model) which moves a rank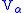
of the cumulative hierarchy
of sets. We may suppose without loss of generality that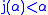
. We talk about the automorphism
moving the rank rather than the ordinal because we do not want to assume that every ordinal in the model is the index of a rank.
The domain of the model of NFU will be the nonstandard rank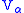
. The membership relation of the model of NFU will be
We now prove that this actually is a model of NFU. Let
be a stratified formula in the language of NFU. Choose an assignment of types to all variables in the formula which witnesses the fact that it is stratified. Choose a natural number N greater than all types assigned to variables by this stratification.
Expand the formula
into a formula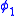 
in the language of the nonstandard model of Zermelo set theory
with automorphism
j using the definition of membership in the model of NFU. Application of any power of j to both sides of an equation or membership statement preserves its truth value because j is an automorphism. Make such an application to each atomic formula
in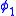
in such a way that each variable x assigned type i occurs with exactly 
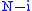applications of j. This is possible thanks to the form of the atomic membership statements derived from NFU membership statements, and to the formula being stratified. Each quantified sentence 
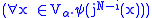can be converted to the form 
(and similarly for existential quantifiers). Carry out this transformation everywhere and obtain a formula 
in which j is never applied to a bound variable.
Choose any free variable y in
assigned type i. Apply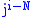 
uniformly to the entire formula to obtain a formula 
in which y appears without any application of j. Now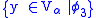 
exists (because j appears applied only to free variables and constants), belongs to 
, and contains exactly those y which satisfy the original formula
in the model of NFU. 
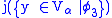has this extension in the model of NFU (the application of j corrects for the different definition of membership in the model of NFU). This establishes that Stratified Comprehension holds in the model of NFU.
To see that weak Extensionality holds is straightforward: each nonempty element of
inherits a unique extension from the nonstandard model, the empty set inherits its usual extension as well, and all other objects are urelements.
The basic idea is that the automorphism j codes the "power set"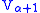
of our "universe" 
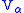into its externally isomorphic copy 
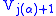inside our "universe." The remaining objects not coding subsets of the universe are treated as urelements.
If
is a natural number n, we get a model of NFU which claims that the universe is finite (it is externally infinite, of course). If 
is infinite and the Choice holds in the nonstandard model of ZFC, we obtain a model of NFU + Infinity + Choice.
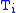(all of the same type in the metatheory) with embeddings of each 
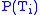into 
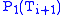coding embeddings of the power set of 
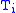into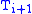 
in a type-respecting manner). Given an embedding of 
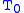into 
(identifying elements of the base "type" with subsets of the base type), one can define embeddings from each "type" into its successor in a natural way. This can be generalized to transfinite sequences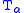 
with care.
Note that the construction of such sequences of sets is limited by the size of the type in which they are being constructed; this prevents TSTU from proving its own consistency (TSTU + Infinity can prove the consistency of TSTU; to prove the consistency of TSTU+Infinity one needs a type containing a set of cardinality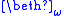
, which cannot be proved to exist in TSTU+Infinity without stronger assumptions). Now the same results of model theory can be used to build a model of NFU and verify that it is a model of NFU in much the same way, with the 
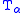's being used in place of 
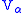in the usual construction. The final move is to observe that since NFU is consistent, we can drop the use of absolute types in our metatheory, bootstrapping the metatheory from TSTU to NFU.
Facts about the automorphism
The automorphism
j of a model of this kind is closely related to certain natural operations in NFU. For example, if W is a well-ordering in the nonstandard model (we suppose here that we use Kuratowski pairs
so that the coding of functions in the two theories will agree to some extent) which is also a well-ordering in NFU (all well-orderings of NFU are well-orderings in the nonstandard model of Zermelo set theory, but not vice versa, due to the formation of urelements in the construction of the model), and W has type α in NFU, then j(W) will be a well-ordering of type T(α) in NFU.
In fact, j is coded by a function in the model of NFU. The function in the nonstandard model which sends the singleton of any element of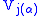
to its sole element, becomes in NFU a function which sends each singleton {x}, where x is any object in the universe, to j(x). Call this function Endo and let it have the following properties: Endo is an injection
from the set of singletons into the set of sets, with the property that Endo( {x} ) = {Endo( {y} ) | y∈x} for each set x. This function can define a type level "membership" relation on the universe, one reproducing the membership relation of the original nonstandard model.
One can add to this base theory strong axioms of infinity familiar from the ZFC context, such as "there exists an inaccessible cardinal," but it is more natural to consider assertions about cantorian and strongly cantorian sets. Such assertions not only bring into being large cardinals of the usual sorts, but strengthen the theory on its own terms.
The weakest of the usual strong principles is:
To see how natural numbers are defined in NFU, see set-theoretic definition of natural numbers
. The original form of this axiom given by Rosser was "the set {m|1≤m≤n} has n members", for each natural number n". This intuitively obvious assertion is unstratified: what is provable in NFU is "the set {m|1≤m≤n} has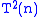
members" (where the T operation on cardinals is defined by 
; this raises the type of a cardinal by one). For any cardinal number (including natural numbers) to assert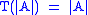 
is equivalent to asserting that the sets A of that cardinality are cantorian (by a usual abuse of language, we refer to such cardinals as "cantorian cardinals"). It is straightforward to show that the assertion that each natural number is cantorian is equivalent to the assertion that the set of all natural numbers is strongly cantorian.
Counting is consistent with NFU, but increases its consistency strength noticeably; not, as one would expect, in the area of arithmetic, but in higher set theory. NFU + Infinity proves that each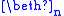
exists, but not that 
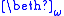exists; NFU + Counting (easily) proves Infinity, and further proves the existence of 
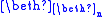for each n, but not the existence of 
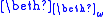. (See beth number
s).
Counting implies immediately that one does not need to assign types to variables restricted to the set
of natural numbers for purposes of stratification; it is a theorem that the power set of a strongly cantorian set is strongly cantorian, so it is further not necessary to assign types to variables restricted to any iterated power set of the natural numbers, or to such familiar sets as the set of real numbers, the set of functions from reals to reals, and so forth. The set-theoretical strength of Counting is less important in practice than the convenience of not having to annotate variables known to have natural number values (or related kinds of values) with singleton brackets, or to apply the T operation in order to get stratified set definitions.
Counting implies Infinity; each of the axioms below needs to be adjoined to NFU + Infinity to get the effect of strong variants of Infinity; Ali Enayat has investigated the strength of some of these axioms in models of NFU + "the universe is finite".
A model of the kind constructed above satisfies Counting just in case the automorphism j fixes all natural numbers in the underlying nonstandard model of Zermelo set theory.
The next strong axiom we consider is the
Immediate consequences include Mathematical Induction for unstratified conditions (which is not a consequence of Counting; many but not all unstratified instances of induction on the natural numbers follow from Counting).
This axiom is surprisingly strong. Unpublished work of Robert Solovay shows that the consistency strength of the theory NFU* = NFU + Counting + Strongly Cantorian Separation is the same as that of Zermelo set theory +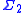
Replacement.
This axiom holds in a model of the kind constructed above (with Choice) if the ordinals which are fixed by j and dominate only ordinals fixed by j in the underlying nonstandard model of Zermelo set theory are standard, and the power set of any such ordinal in the model is also standard. This condition is sufficient but not necessary.
Next is
This very simple and appealing assertion is extremely strong. Solovay has shown the precise equivalence of the consistency strength of the theory NFUA = NFU + Infinity + Cantorian Sets with that of ZFC + a schema asserting the existence of an n-Mahlo cardinal for each concrete natural number n. Ali Enayat has shown that the theory of cantorian equivalence classes of well-founded extensional relations (which gives a natural picture of an initial segment of the cumulative hierarchy of ZFC) interprets the extension of ZFC with n-Mahlo cardinals directly. A permutation technique can be applied to a model of this theory to give a model in which the hereditarily strongly cantorian sets with the usual membership relation model the strong extension of ZFC.
This axiom holds in a model of the kind constructed above (with Choice) just in case the ordinals fixed by j in the underlying nonstandard model of ZFC are an initial (proper class) segment of the ordinals of the model.
Next consider the
This combines the effect of the two preceding axioms and is actually even stronger (precisely how is not known). Unstratified mathematical induction enables proving that there are n-Mahlo cardinals for every n, given Cantorian Sets, which gives an extension of ZFC that is even stronger than the previous one, which only asserts that there are n-Mahlos for each concrete natural number (leaving open the possibility of nonstandard counterexamples).
This axiom will hold in a model of the kind described above if every ordinal fixed by j is standard, and every power set of an ordinal fixed by j is also standard in the underlying model of ZFC. Again, this condition is sufficient but not necessary.
An ordinal is said to be cantorian if it is fixed by T, and strongly cantorian if it dominates only cantorian ordinals (this implies that it is itself cantorian). In models of the kind constructed above, cantorian ordinals of NFU correspond to ordinals fixed by j (they are not the same objects because different definitions of ordinal numbers are used in the two theories).
Equal in strength to Cantorian Sets is the
Recall that
is the order type of the natural order on all ordinals. This only implies Cantorian Sets if we have Choice (but is at that level of consistency strength in any case). It is remarkable that one can even define 
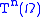: this is the nth term 
of any finite sequence of ordinals s of length n such that 
, 
for each appropriate i. This definition is completely unstratified. The uniqueness of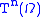 
can be proved (for those n for which it exists) and a certain amount of common-sense reasoning about this notion can be carried out, enough to show that Large Ordinals implies Cantorian Sets in the presence of Choice. In spite of the knotty formal statement of this axiom, it is a very natural assumption, amounting to making the action of T on the ordinals as simple as possible.
A model of the kind constructed above will satisfy Large Ordinals, if the ordinals moved by j are exactly the ordinals which dominate some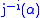
in the underlying nonstandard model of ZFC.
Solovay has shown the precise equivalence in consistency strength of NFUB = NFU + Infinity + Cantorian Sets + Small Ordinals with Morse–Kelley set theory
plus the assertion that the proper class ordinal (the class of all ordinals) is a weakly compact cardinal
. This is very strong indeed! Moreover, NFUB-, which is NFUB with Cantorian Sets omitted, is easily seen to have the same strength as NFUB.
A model of the kind constructed above will satisfy this axiom if every collection of ordinals fixed by j is the intersection of some set of ordinals with the ordinals fixed by j, in the underlying nonstandard model of ZFC.
Even stronger is the theory NFUM = NFU + Infinity + Large Ordinals + Small Ordinals. This is equivalent to Morse–Kelley set theory
with a predicate on the classes which is a κ-complete nonprincipal ultrafilter
on the proper class ordinal κ; in effect, this is Morse–Kelley set theory + "the proper class ordinal is a measurable cardinal
"!
The technical details here are not the main point, which is that reasonable and natural (in the context of NFU) assertions turn out to be equivalent in power to very strong axioms of infinity in the ZFC context. This fact is related to the correlation between the existence of models of NFU, described above and satisfying these axioms, and the existence of models of ZFC with automorphism
s having special properties.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, New Foundations (NF) is an axiomatic set theory, conceived by Willard Van Orman Quine
Willard Van Orman Quine
Willard Van Orman Quine was an American philosopher and logician in the analytic tradition...
as a simplification of the theory of types of Principia Mathematica
Principia Mathematica
The Principia Mathematica is a three-volume work on the foundations of mathematics, written by Alfred North Whitehead and Bertrand Russell and published in 1910, 1912, and 1913...
. Quine first proposed NF in a 1937 article titled "New Foundations for Mathematical Logic"; hence the name. Much of this entry discusses NFU, an important variant of NF due to Jensen (1969) and exposited in Holmes (1998).
The type theory TST
The primitive predicates of TST, a streamlined version of the theory of typesType theory
In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
, are equality (
) and membership (). TST has a linear hierarchy of types: type 0 consists of individuals otherwise undescribed. For each (meta-) natural number n, type n+1 objects are sets of type n objects; sets of type n have members of type n-1. Objects connected by identity must have the same type. The following two atomic formulas succinctly describe the typing rules: and 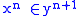(notation to be improved).The axioms of TST are:
- ExtensionalityAxiom of extensionalityIn axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of extensionality, or axiom of extension, is one of the axioms of Zermelo-Fraenkel set theory.- Formal statement :...
: sets of the same (positive) type with the same members are equal; - An axiom schema of comprehension, namely:
- If
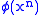is a formulaWell-formed formulaIn mathematical logic, a well-formed formula, shortly wff, often simply formula, is a word which is part of a formal language...
, then the set
exists.
- In other words, given any formula
, the formula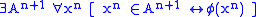 
is an axiom where 
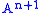represents the set 
.
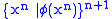This type theory is much less complicated than the one first set out in the Principia Mathematica
Principia Mathematica
The Principia Mathematica is a three-volume work on the foundations of mathematics, written by Alfred North Whitehead and Bertrand Russell and published in 1910, 1912, and 1913...
, which included types for relations
Relation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
whose arguments were not necessarily all of the same type. In 1914, Norbert Wiener
Norbert Wiener
Norbert Wiener was an American mathematician.A famous child prodigy, Wiener later became an early researcher in stochastic and noise processes, contributing work relevant to electronic engineering, electronic communication, and control systems.Wiener is regarded as the originator of cybernetics, a...
showed how to code the ordered pair
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
as a set of sets, making it possible to eliminate relation types in favor of the linear hierarchy of sets described here.
Axioms and stratification
New Foundations (NF) is obtained from TST by abandoning the distinctions of type. The axioms of NF are:- ExtensionalityExtensionalityIn logic, extensionality, or extensional equality refers to principles that judge objects to be equal if they have the same external properties...
: Two objects with the same elements are the same object; - A comprehension schema: All instances of TST Comprehension but with type indices dropped (and without introducing new identifications between variables).
By convention, NF's Comprehension schema is stated using the concept of stratified formula and making no direct reference to types. A formula
is said to be stratified if there exists a functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f from pieces of syntax to the natural numbers, such that for any atomic subformula
of we have f(y) = f(x) + 1, while for any atomic subformula of , we have f(x) = f(y). Comprehension then becomes: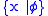 exists for each stratified formula .Even the indirect reference to types implicit in the notion of stratification
Stratification (mathematics)
-In mathematical logic:In mathematical logic, stratification is any consistent assignment of numbers to predicate symbols guaranteeing that a unique formal interpretation of a logical theory exists...
can be eliminated. Theodore Hailperin showed in 1944 that Comprehension is equivalent to a finite conjunction of its instances, so that NF can be finitely axiomatized without any reference to the notion of type.
Comprehension may seem to run afoul of problems similar to those in naive set theory
Naive set theory
Naive set theory is one of several theories of sets used in the discussion of the foundations of mathematics. The informal content of this naive set theory supports both the aspects of mathematical sets familiar in discrete mathematics , and the everyday usage of set theory concepts in most...
, but this is not the case. For example, the impossible Russell class
Russell's paradox
In the foundations of mathematics, Russell's paradox , discovered by Bertrand Russell in 1901, showed that the naive set theory created by Georg Cantor leads to a contradiction...
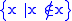is not an NF set, because 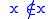cannot be stratified.Ordered pairs
RelationsRelation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
and functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
are defined in TST (and in NF and NFU) as sets of ordered pair
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
s in the usual way. The usual definition of the ordered pair, first proposed by Kuratowski in 1921, has a serious drawback for NF and related theories: the resulting ordered pair necessarily has a type two higher than the type of its arguments (its left and right projection
Projection (mathematics)
Generally speaking, in mathematics, a projection is a mapping of a set which is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows...
s). Hence for purposes of determining stratification, a function is three types higher than the members of its field.
If one can define a pair in such a way that its type is the same type as that of its arguments (resulting in a type-level ordered pair), then a relation or function is merely one type higher than the type of the members of its field. Hence NF and related theories usually employ Quine
Willard Van Orman Quine
Willard Van Orman Quine was an American philosopher and logician in the analytic tradition...
's set-theoretic definition of the ordered pair, which yields a type-level ordered pair. Holmes (1998) takes the ordered pair and its left and right projection
Projection (mathematics)
Generally speaking, in mathematics, a projection is a mapping of a set which is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows...
s as primitive. Fortunately, whether the ordered pair is type-level by definition or by assumption (i.e., taken as primitive) usually does not matter.
The existence of a type-level ordered pair implies Infinity, and NFU + Infinity interprets NFU + "there is a type level ordered pair" (they are not quite the same theory, but the differences are inessential). Conversely, NFU + Infinity + Choice proves the existence of a type-level ordered pair.
Admissibility of useful large sets
NF (and NFU + Infinity + Choice, described below and known consistent) allow the construction of two kinds of sets that ZFC and its proper extensions disallow because they are "too large" (some set theories admit these entities under the heading of proper classes):- The universal setUniversal setIn set theory, a universal set is a set which contains all objects, including itself. In set theory as usually formulated, the conception of a set of all sets leads to a paradox...
V. Because
is a stratified formula, the universal setUniversal setIn set theory, a universal set is a set which contains all objects, including itself. In set theory as usually formulated, the conception of a set of all sets leads to a paradox...
V = {x | x=x} exists by Comprehension. An immediate consequence is that all sets have complementsComplement (set theory)In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
, and the entire set-theoretic universe under NF has a Boolean structure. - CardinalCardinal numberIn mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
and ordinalOrdinal numberIn set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
numbers. In NF (and TST), the set of all sets having n elements (the circularityCircular reasoningCircular reasoning, or in other words, paradoxical thinking, is a type of formal logical fallacy in which the proposition to be proved is assumed implicitly or explicitly in one of the premises. For example:"Only an untrustworthy person would run for office...
here is only apparent) exists. Hence Frege's definition of the cardinal numbers works in NF and NFU: a cardinal number is an equivalence class of sets under the relationRelation (mathematics)In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
of equinumerosityEquinumerosityIn mathematics, two sets are equinumerous if they have the same cardinality, i.e., if there exists a bijection f : A → B for sets A and B. This is usually denoted A \approx B \, or A \sim B....
: the sets A and B are equinumerous if there exists a bijectionBijectionA bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
between them, in which case we write
. Likewise, an ordinal number is an equivalence class of well-ordered sets.
Finite axiomatizability
New Foundations can be finitely axiomatized. Two such formulations are given here.Cartesian closure
Unfortunately, the category whose objects are the sets of NF and whose morphisms are the functions between those sets is not cartesian closedCartesian closed category
In category theory, a category is cartesian closed if, roughly speaking, any morphism defined on a product of two objects can be naturally identified with a morphism defined on one of the factors. These categories are particularly important in mathematical logic and the theory of programming, in...
; this is a highly desirable property for any set theory to have. Intuitively, it means that the functions of NF do not curry
Currying
In mathematics and computer science, currying is the technique of transforming a function that takes multiple arguments in such a way that it can be called as a chain of functions each with a single argument...
as one would normally expect functions to. Furthermore, it means that NF is not a topos
Topos
In mathematics, a topos is a type of category that behaves like the category of sheaves of sets on a topological space...
.
The consistency problem and related partial results
The outstanding problem with NF is that it is not known to be relatively consistentEquiconsistency
In mathematical logic, two theories are equiconsistent if, roughly speaking, they are "as consistent as each other".It is not in general possible to prove the absolute consistency of a theory T...
to any mainstream mathematical system. NF disproves Choice, and so proves Infinity (Specker, 1953). But it is also known (Jensen
Ronald Jensen
Ronald Björn Jensen is an American mathematician active in Europe, primarily known for his work in mathematical logic and set theory.-Career:...
, 1969) that the minor(?) modification of allowing urelements (objects lacking members which are distinct from the empty set and from one another) yields NFU, a theory that is consistent relative to Peano arithmetic; if Infinity and Choice are added, the resulting theory has the same consistency strength as type theory with infinity or bounded Zermelo set theory. (NFU corresponds to a type theory TSTU, where positive types may contain urelements.) There are other relatively consistent variants of NF.
NFU is, roughly speaking, weaker than NF because in NF, the power set of the universe is the universe itself, while in NFU, the power set of the universe may be strictly smaller than the universe (the power set of the universe contains only sets, while the universe may contain urelements). In fact, this is necessarily the case in NFU+"Choice".
Specker has shown that NF is equiconsistent
Equiconsistency
In mathematical logic, two theories are equiconsistent if, roughly speaking, they are "as consistent as each other".It is not in general possible to prove the absolute consistency of a theory T...
with TST + Amb, where Amb is the axiom scheme of typical ambiguity which asserts
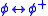for any formula , 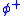being the formula obtained by raising every type index in by one. NF is also equiconsistent with the theory TST augmented with a "type shifting automorphism", an operation which raises type by one, mapping each type onto the next higher type, and preserves equality and membership relations (and which cannot be used in instances of Comprehension: it is external to the theory). The same results hold for various fragments of TST in relation to the corresponding fragments of NF.In the same year (1969) that Jensen
Ronald Jensen
Ronald Björn Jensen is an American mathematician active in Europe, primarily known for his work in mathematical logic and set theory.-Career:...
proved NFU consistent, Grishin proved
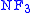consistent. 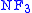is the fragment of NF with full extensionality (no urelements) and those instances of Comprehension which can be stratified using just three types. This theory is a very awkward medium for mathematics (although there have been attempts to alleviate this awkwardness), largely because there is no obvious definition for an ordered pairOrdered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
. Despite this awkwardness,
is very interesting because every infinite model of TST restricted to three types satisfies Amb. Hence for every such model there is a model of 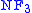with the same theory. This does not hold for four types: 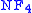is the same theory as NF, and we have no idea how to obtain a model of TST with four types in which Amb holds.In 1983, Marcel Crabbé proved consistent a system he called NFI, whose axioms are unrestricted extensionality and those instances of Comprehension in which no variable is assigned a type higher than that of the set asserted to exist. This is a predicativity
Impredicative
In mathematics and logic, impredicativity is the property of a self-referencing definition. More precisely, a definition is said to be impredicative if it invokes the set being defined, or another set which contains the thing being defined.Russell's paradox is a famous example of an impredicative...
restriction, though NFI is not a predicative theory: it admits enough impredicativity to define the set of natural numbers (defined as the intersection of all inductive sets; note that the inductive sets quantified over are of the same type as the set of natural numbers being defined). Crabbé also discussed a subtheory of NFI, in which only parameters (free variables) are allowed to have the type of the set asserted to exist by an instance of Comprehension. He called the result "predicative NF" (NFP); it is, of course, doubtful whether any theory with a self-membered universe is truly predicative. Holmes has
Principia Mathematica
The Principia Mathematica is a three-volume work on the foundations of mathematics, written by Alfred North Whitehead and Bertrand Russell and published in 1910, 1912, and 1913...
without the Axiom of Reducibility
Reduction (complexity)
In computability theory and computational complexity theory, a reduction is a transformation of one problem into another problem. Depending on the transformation used this can be used to define complexity classes on a set of problems....
.
How NF(U) avoids the set-theoretic paradoxes
NF steers clear of the three well-known paradoxParadox
Similar to Circular reasoning, A paradox is a seemingly true statement or group of statements that lead to a contradiction or a situation which seems to defy logic or intuition...
es of set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
. That NFU, a {relatively} consistent theory, also avoids the paradoxes increases our confidence in this fact.
The Russell paradox: An easy matter;
is not a stratified formula, so the existence of 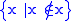is not asserted by any instance of Comprehension. Quine presumably constructed NF with this paradox uppermost in mind.Cantor's paradox
Cantor's paradox
In set theory, Cantor's paradox is derivable from the theorem that there is no greatest cardinal number, so that the collection of "infinite sizes" is itself infinite...
of the largest cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
exploits the application of Cantor's theorem
Cantor's theorem
In elementary set theory, Cantor's theorem states that, for any set A, the set of all subsets of A has a strictly greater cardinality than A itself...
to the universal set
Universal set
In set theory, a universal set is a set which contains all objects, including itself. In set theory as usually formulated, the conception of a set of all sets leads to a paradox...
. Cantor's theorem
Cantor's theorem
In elementary set theory, Cantor's theorem states that, for any set A, the set of all subsets of A has a strictly greater cardinality than A itself...
says (given ZFC) that the power set
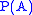of any set is larger than (there can be no injectionInjective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
(one-to-one map) from
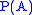into ). Now of course there is an injectionInjective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
from
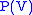into , if is the universal set! The resolution requires that we observe that makes no sense in the theory of types: the type of 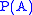is one higher than the type of . The correctly typed version (which is a theorem in the theory of types for essentially the same reasons that the original form of Cantor's theoremCantor's theorem
In elementary set theory, Cantor's theorem states that, for any set A, the set of all subsets of A has a strictly greater cardinality than A itself...
works in ZF
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
) is
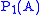, where is the set of one-element subsets of . The specific instance of this theorem that interests us is : there are fewer one-element sets than sets (and so fewer one-element sets than general objects, if we are in NFU). The "obvious" bijectionBijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
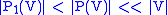from the universe to the one-element sets is not a set; it is not a set because its definition is unstratified. Note that in all known models of NFU it is the case that ; Choice allows one not only to prove that there are urelements but that there are many cardinals between 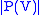and 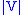.We now introduce some useful notions. A set
which satisfies the intuitively appealing is said to be cantorian: a cantorian set satisfies the usual form of Cantor's theoremCantor's theorem
In elementary set theory, Cantor's theorem states that, for any set A, the set of all subsets of A has a strictly greater cardinality than A itself...
. A set
which satisfies the further condition that 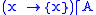, the restrictionRestriction
Restriction may refer to:* Restriction , an aspect of a mathematical function* Restrictions , an album by Cactus* Restriction enzyme, a type of enzyme that cleaves genetic material...
of the singleton map to A, is not only cantorian set but strongly cantorian.
The Burali-Forti paradox
Burali-Forti paradox
In set theory, a field of mathematics, the Burali-Forti paradox demonstrates that naively constructing "the set of all ordinal numbers" leads to a contradiction and therefore shows an antinomy in a system that allows its construction...
of the largest ordinal number
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
goes as follows. We define (following naive set theory
Naive set theory
Naive set theory is one of several theories of sets used in the discussion of the foundations of mathematics. The informal content of this naive set theory supports both the aspects of mathematical sets familiar in discrete mathematics , and the everyday usage of set theory concepts in most...
) the ordinals as equivalence classes of well-orderings under similarity
Similarity
-Specific definitions:Different fields provide differing definitions of similarity:-In computer science:* string metric, aka string similarity* semantic similarity in computational linguistics-In other fields:...
. There is an obvious natural well-ordering on the ordinals; since it is a well-ordering it belongs to an ordinal
. It is straightforward to prove (by transfinite inductionTransfinite induction
Transfinite induction is an extension of mathematical induction to well-ordered sets, for instance to sets of ordinal numbers or cardinal numbers.- Transfinite induction :Let P be a property defined for all ordinals α...
) that the order type of the natural order on the ordinals less than a given ordinal
is itself. But this means that is the order type of the ordinals 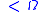and so is strictly less than the order type of all the ordinals — but the latter is, by definition, itself!The solution to the paradox in NF(U) starts with the observation that the order type of the natural order on the ordinals less than
is of a higher type than . Hence a type level ordered pairOrdered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
is two, and the usual Kuratowski ordered pair, four, types higher than the type of its arguments. For any order type
, we can define an order type one type higher: if , then 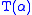is the order type of the order 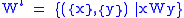. The triviality of the T operation is only a seeming one; it is easy to show that T is a strictly monotoneMonotone
Monotone refers to a sound, for example speech or music, that has a single unvaried tone.Monotone or monotonicity may also refer to:*Monotone , an open source revision control system*Monotone class theorem, in measure theory...
(order preserving) operation on the ordinals.
We can now restate the lemma on order types in a stratified manner: the order type of the natural order on the ordinals
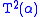is or depending on which pair is used (we assume the type level pair hereinafter). From this we deduce that the order type on the ordinals
is 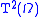, from which we deduce 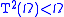. Hence the T operation is not a function; we cannot have a strictly monotoneMonotone
Monotone refers to a sound, for example speech or music, that has a single unvaried tone.Monotone or monotonicity may also refer to:*Monotone , an open source revision control system*Monotone class theorem, in measure theory...
set map from ordinals to ordinals which sends an ordinal downward! Since T is monotone, we have
, a "descending sequence" in the ordinals which cannot be a set.Some have asserted that this result shows that no model of NF(U) is "standard", since the ordinals in any model of NFU are externally not well-ordered. We do not take a position on this, but we note that it is also a theorem of NFU that any set model of NFU has non-well-ordered "ordinals"; NFU does not conclude that the universe V is a model of NFU, despite V being a set, because the membership relation is not a set relation.
For a further development of mathematics in NFU
NFU
NFU is a three-letter acronym which may stand for:* National Farmers Union* New Foundations with Urelements* National Formosa University, a University in Taiwan* Nuclear No first use policy...
, with a comparison to the development of the same in ZFC, see implementation of mathematics in set theory
Implementation of mathematics in set theory
This article examines the implementation of mathematical concepts in set theory. The implementation of a number of basic mathematical concepts is carried out in parallel in ZFC and in NFU, the version of Quine's New Foundations shown to be consistent by R. B...
.
The set theory of the 1940 first edition of Quine
Willard Van Orman Quine
Willard Van Orman Quine was an American philosopher and logician in the analytic tradition...
's Mathematical Logic married NF to the proper classes of NBG set theory, and included an axiom schema of unrestricted comprehension for proper classes. In 1942, J. Barkley Rosser proved that the system presented in Mathematical Logic was subject to the Burali-Forti paradox. This result does not apply to NF. In 1950, Hao Wang showed how to amend Quine's axioms so as to avoid this problem, and Quine included the resulting axiomatization in the 1951 second and final edition of Mathematical Logic.
Models of NFU
There is a fairly simple method for producing models of NFU in bulk. Using well-known techniques of model theoryModel theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, one can construct a nonstandard model of Zermelo set theory
Zermelo set theory
Zermelo set theory, as set out in an important paper in 1908 by Ernst Zermelo, is the ancestor of modern set theory. It bears certain differences from its descendants, which are not always understood, and are frequently misquoted...
(nothing nearly as strong as full ZFC is needed for the basic technique) on which there is an external automorphism j (not a set of the model) which moves a rank
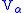of the cumulative hierarchyHierarchy
A hierarchy is an arrangement of items in which the items are represented as being "above," "below," or "at the same level as" one another...
of sets. We may suppose without loss of generality that
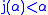. We talk about the automorphismAutomorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
moving the rank rather than the ordinal because we do not want to assume that every ordinal in the model is the index of a rank.
The domain of the model of NFU will be the nonstandard rank
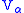. The membership relation of the model of NFU will be
We now prove that this actually is a model of NFU. Let
be a stratified formula in the language of NFU. Choose an assignment of types to all variables in the formula which witnesses the fact that it is stratified. Choose a natural number N greater than all types assigned to variables by this stratification.Expand the formula
into a formula 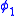in the language of the nonstandard model of Zermelo set theoryZermelo set theory
Zermelo set theory, as set out in an important paper in 1908 by Ernst Zermelo, is the ancestor of modern set theory. It bears certain differences from its descendants, which are not always understood, and are frequently misquoted...
with automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
j using the definition of membership in the model of NFU. Application of any power of j to both sides of an equation or membership statement preserves its truth value because j is an automorphism. Make such an application to each atomic formula
Atomic formula
In mathematical logic, an atomic formula is a formula with no deeper propositional structure, that is, a formula that contains no logical connectives or equivalently a formula that has no strict subformulas. Atoms are thus the simplest well-formed formulas of the logic...
in
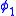in such a way that each variable x assigned type i occurs with exactly 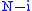applications of j. This is possible thanks to the form of the atomic membership statements derived from NFU membership statements, and to the formula being stratified. Each quantified sentence 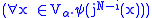can be converted to the form (and similarly for existential quantifiers). Carry out this transformation everywhere and obtain a formula in which j is never applied to a bound variable.Choose any free variable y in
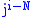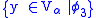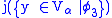assigned type i. Apply uniformly to the entire formula to obtain a formula in which y appears without any application of j. Now exists (because j appears applied only to free variables and constants), belongs to , and contains exactly those y which satisfy the original formula in the model of NFU. has this extension in the model of NFU (the application of j corrects for the different definition of membership in the model of NFU). This establishes that Stratified Comprehension holds in the model of NFU.To see that weak Extensionality holds is straightforward: each nonempty element of
inherits a unique extension from the nonstandard model, the empty set inherits its usual extension as well, and all other objects are urelements.The basic idea is that the automorphism j codes the "power set"
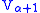of our "universe" 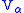into its externally isomorphic copy 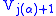inside our "universe." The remaining objects not coding subsets of the universe are treated as urelements.If
is a natural number n, we get a model of NFU which claims that the universe is finite (it is externally infinite, of course). If is infinite and the Choice holds in the nonstandard model of ZFC, we obtain a model of NFU + Infinity + Choice.Self-sufficiency of mathematical foundations in NFU
For philosophical reasons, it is important to note that it is not necessary to work in ZFC or any related system to carry out this proof. A common argument against the use of NFU as a foundation for mathematics is that our reasons for relying on it have to do with our intuition that ZFC is correct. We claim that it is sufficient to accept TST (in fact TSTU). 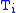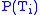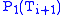We outline the approach: take the type theory TSTU (allowing urelements in each positive type) as our metatheory and consider the theory of set models of TSTU in TSTU (these models will be sequences of sets (all of the same type in the metatheory) with embeddings of each into coding embeddings of the power set of 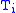into 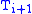in a type-respecting manner). Given an embedding of 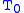into (identifying elements of the base "type" with subsets of the base type), one can define embeddings from each "type" into its successor in a natural way. This can be generalized to transfinite sequences 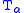with care.Note that the construction of such sequences of sets is limited by the size of the type in which they are being constructed; this prevents TSTU from proving its own consistency (TSTU + Infinity can prove the consistency of TSTU; to prove the consistency of TSTU+Infinity one needs a type containing a set of cardinality
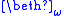, which cannot be proved to exist in TSTU+Infinity without stronger assumptions). Now the same results of model theory can be used to build a model of NFU and verify that it is a model of NFU in much the same way, with the 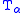's being used in place of 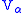in the usual construction. The final move is to observe that since NFU is consistent, we can drop the use of absolute types in our metatheory, bootstrapping the metatheory from TSTU to NFU. Facts about the automorphismAutomorphismIn mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
j
The automorphismAutomorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
j of a model of this kind is closely related to certain natural operations in NFU. For example, if W is a well-ordering in the nonstandard model (we suppose here that we use Kuratowski pairs
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
so that the coding of functions in the two theories will agree to some extent) which is also a well-ordering in NFU (all well-orderings of NFU are well-orderings in the nonstandard model of Zermelo set theory, but not vice versa, due to the formation of urelements in the construction of the model), and W has type α in NFU, then j(W) will be a well-ordering of type T(α) in NFU.
In fact, j is coded by a function in the model of NFU. The function in the nonstandard model which sends the singleton of any element of
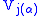to its sole element, becomes in NFU a function which sends each singleton {x}, where x is any object in the universe, to j(x). Call this function Endo and let it have the following properties: Endo is an injectionInjective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
from the set of singletons into the set of sets, with the property that Endo( {x} ) = {Endo( {y} ) | y∈x} for each set x. This function can define a type level "membership" relation on the universe, one reproducing the membership relation of the original nonstandard model.
Strong axioms of Infinity
In this section we mainly discuss the effect of adding various "strong axioms of infinity" to our usual base theory, NFU + Infinity + Choice. This base theory, known consistent, has the same strength as TST + Infinity, or Zermelo set theory with Separation restricted to bounded formulas (Mac Lane set theory).One can add to this base theory strong axioms of infinity familiar from the ZFC context, such as "there exists an inaccessible cardinal," but it is more natural to consider assertions about cantorian and strongly cantorian sets. Such assertions not only bring into being large cardinals of the usual sorts, but strengthen the theory on its own terms.
The weakest of the usual strong principles is:
- Rosser's Axiom of Counting. The set of natural numbers is a strongly cantorian set.
To see how natural numbers are defined in NFU, see set-theoretic definition of natural numbers
Set-theoretic definition of natural numbers
Several ways have been proposed to define the natural numbers using set theory.- The contemporary standard :In standard, Zermelo-Fraenkel set theory the natural numbers...
. The original form of this axiom given by Rosser was "the set {m|1≤m≤n} has n members", for each natural number n". This intuitively obvious assertion is unstratified: what is provable in NFU is "the set {m|1≤m≤n} has
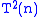members" (where the T operation on cardinals is defined by ; this raises the type of a cardinal by one). For any cardinal number (including natural numbers) to assert 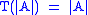is equivalent to asserting that the sets A of that cardinality are cantorian (by a usual abuse of language, we refer to such cardinals as "cantorian cardinals"). It is straightforward to show that the assertion that each natural number is cantorian is equivalent to the assertion that the set of all natural numbers is strongly cantorian.Counting is consistent with NFU, but increases its consistency strength noticeably; not, as one would expect, in the area of arithmetic, but in higher set theory. NFU + Infinity proves that each
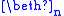exists, but not that 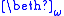exists; NFU + Counting (easily) proves Infinity, and further proves the existence of 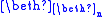for each n, but not the existence of 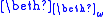. (See beth numberBeth number
In mathematics, the infinite cardinal numbers are represented by the Hebrew letter \aleph indexed with a subscript that runs over the ordinal numbers...
s).
Counting implies immediately that one does not need to assign types to variables restricted to the set
of natural numbers for purposes of stratification; it is a theorem that the power set of a strongly cantorian set is strongly cantorian, so it is further not necessary to assign types to variables restricted to any iterated power set of the natural numbers, or to such familiar sets as the set of real numbers, the set of functions from reals to reals, and so forth. The set-theoretical strength of Counting is less important in practice than the convenience of not having to annotate variables known to have natural number values (or related kinds of values) with singleton brackets, or to apply the T operation in order to get stratified set definitions.Counting implies Infinity; each of the axioms below needs to be adjoined to NFU + Infinity to get the effect of strong variants of Infinity; Ali Enayat has investigated the strength of some of these axioms in models of NFU + "the universe is finite".
A model of the kind constructed above satisfies Counting just in case the automorphism j fixes all natural numbers in the underlying nonstandard model of Zermelo set theory.
The next strong axiom we consider is the
- Axiom of strongly cantorian separation: For any strongly cantorian set A and any formula
(not necessarily stratified!) the set {x∈A|φ} exists.
Immediate consequences include Mathematical Induction for unstratified conditions (which is not a consequence of Counting; many but not all unstratified instances of induction on the natural numbers follow from Counting).
This axiom is surprisingly strong. Unpublished work of Robert Solovay shows that the consistency strength of the theory NFU* = NFU + Counting + Strongly Cantorian Separation is the same as that of Zermelo set theory +
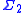Replacement.This axiom holds in a model of the kind constructed above (with Choice) if the ordinals which are fixed by j and dominate only ordinals fixed by j in the underlying nonstandard model of Zermelo set theory are standard, and the power set of any such ordinal in the model is also standard. This condition is sufficient but not necessary.
Next is
- Axiom of Cantorian Sets: Every cantorian set is strongly cantorian.
This very simple and appealing assertion is extremely strong. Solovay has shown the precise equivalence of the consistency strength of the theory NFUA = NFU + Infinity + Cantorian Sets with that of ZFC + a schema asserting the existence of an n-Mahlo cardinal for each concrete natural number n. Ali Enayat has shown that the theory of cantorian equivalence classes of well-founded extensional relations (which gives a natural picture of an initial segment of the cumulative hierarchy of ZFC) interprets the extension of ZFC with n-Mahlo cardinals directly. A permutation technique can be applied to a model of this theory to give a model in which the hereditarily strongly cantorian sets with the usual membership relation model the strong extension of ZFC.
This axiom holds in a model of the kind constructed above (with Choice) just in case the ordinals fixed by j in the underlying nonstandard model of ZFC are an initial (proper class) segment of the ordinals of the model.
Next consider the
- Axiom of Cantorian Separation: For any cantorian set A and any formula
(not necessarily stratified!) the set {x∈A|φ} exists.
This combines the effect of the two preceding axioms and is actually even stronger (precisely how is not known). Unstratified mathematical induction enables proving that there are n-Mahlo cardinals for every n, given Cantorian Sets, which gives an extension of ZFC that is even stronger than the previous one, which only asserts that there are n-Mahlos for each concrete natural number (leaving open the possibility of nonstandard counterexamples).
This axiom will hold in a model of the kind described above if every ordinal fixed by j is standard, and every power set of an ordinal fixed by j is also standard in the underlying model of ZFC. Again, this condition is sufficient but not necessary.
An ordinal is said to be cantorian if it is fixed by T, and strongly cantorian if it dominates only cantorian ordinals (this implies that it is itself cantorian). In models of the kind constructed above, cantorian ordinals of NFU correspond to ordinals fixed by j (they are not the same objects because different definitions of ordinal numbers are used in the two theories).
Equal in strength to Cantorian Sets is the
- Axiom of Large Ordinals: For each noncantorian ordinal
, there is a natural number n such that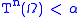 
.
Recall that
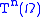is the order type of the natural order on all ordinals. This only implies Cantorian Sets if we have Choice (but is at that level of consistency strength in any case). It is remarkable that one can even define : this is the nth term of any finite sequence of ordinals s of length n such that , for each appropriate i. This definition is completely unstratified. The uniqueness of 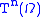can be proved (for those n for which it exists) and a certain amount of common-sense reasoning about this notion can be carried out, enough to show that Large Ordinals implies Cantorian Sets in the presence of Choice. In spite of the knotty formal statement of this axiom, it is a very natural assumption, amounting to making the action of T on the ordinals as simple as possible.A model of the kind constructed above will satisfy Large Ordinals, if the ordinals moved by j are exactly the ordinals which dominate some
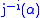in the underlying nonstandard model of ZFC.- Axiom of Small Ordinals: For any formula φ, there is a set A such that the elements of A which are strongly Cantorian ordinals are exactly the strongly cantorian ordinals such that φ.
Solovay has shown the precise equivalence in consistency strength of NFUB = NFU + Infinity + Cantorian Sets + Small Ordinals with Morse–Kelley set theory
Morse–Kelley set theory
In the foundation of mathematics, Morse–Kelley set theory or Kelley–Morse set theory is a first order axiomatic set theory that is closely related to von Neumann–Bernays–Gödel set theory...
plus the assertion that the proper class ordinal (the class of all ordinals) is a weakly compact cardinal
Weakly compact cardinal
In mathematics, a weakly compact cardinal is a certain kind of cardinal number introduced by ; weakly compact cardinals are large cardinals, meaning that their existence can not be proven from the standard axioms of set theory....
. This is very strong indeed! Moreover, NFUB-, which is NFUB with Cantorian Sets omitted, is easily seen to have the same strength as NFUB.
A model of the kind constructed above will satisfy this axiom if every collection of ordinals fixed by j is the intersection of some set of ordinals with the ordinals fixed by j, in the underlying nonstandard model of ZFC.
Even stronger is the theory NFUM = NFU + Infinity + Large Ordinals + Small Ordinals. This is equivalent to Morse–Kelley set theory
Morse–Kelley set theory
In the foundation of mathematics, Morse–Kelley set theory or Kelley–Morse set theory is a first order axiomatic set theory that is closely related to von Neumann–Bernays–Gödel set theory...
with a predicate on the classes which is a κ-complete nonprincipal ultrafilter
Ultrafilter
In the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
on the proper class ordinal κ; in effect, this is Morse–Kelley set theory + "the proper class ordinal is a measurable cardinal
Measurable cardinal
- Measurable :Formally, a measurable cardinal is an uncountable cardinal number κ such that there exists a κ-additive, non-trivial, 0-1-valued measure on the power set of κ...
"!
The technical details here are not the main point, which is that reasonable and natural (in the context of NFU) assertions turn out to be equivalent in power to very strong axioms of infinity in the ZFC context. This fact is related to the correlation between the existence of models of NFU, described above and satisfying these axioms, and the existence of models of ZFC with automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
s having special properties.
See also
- Alternative set theoryAlternative set theoryGenerically, an alternative set theory is an alternative mathematical approach to the concept of set. It is a proposed alternative to the standard set theory.Some of the alternative set theories are:*the theory of semisets...
- Axiomatic set theory
- Implementation of mathematics in set theoryImplementation of mathematics in set theoryThis article examines the implementation of mathematical concepts in set theory. The implementation of a number of basic mathematical concepts is carried out in parallel in ZFC and in NFU, the version of Quine's New Foundations shown to be consistent by R. B...
- Positive set theory
- Set-theoretic definition of natural numbersSet-theoretic definition of natural numbersSeveral ways have been proposed to define the natural numbers using set theory.- The contemporary standard :In standard, Zermelo-Fraenkel set theory the natural numbers...
External links
- http://math.stanford.edu/~feferman/papers/ess.pdf
- Stanford Encyclopedia of PhilosophyStanford Encyclopedia of PhilosophyThe Stanford Encyclopedia of Philosophy is a freely-accessible online encyclopedia of philosophy maintained by Stanford University. Each entry is written and maintained by an expert in the field, including professors from over 65 academic institutions worldwide...
:- Quine's New Foundations — by Thomas Forster.
- Alternative axiomatic set theories — by Randall Holmes.
- Randall Holmes: New Foundations Home Page.
- Randall Holmes: Bibliography of Set Theory with a Universal Set.
- Randall Holmes: Symmetry as a Criterion for Comprehension Motivating Quine’s ‘New Foundations’