Regular cardinal
Encyclopedia
In set theory
, a regular cardinal is a cardinal number
that is equal to its own cofinality
. So, crudely speaking, a regular cardinal is one which cannot be broken into a smaller collection of smaller parts.
(The situation is slightly more complicated in contexts where the axiom of choice might fail; in that case not all cardinals are necessarily the cardinalities of well-ordered sets. In that case, the above definition is restricted to well-orderable cardinals only.) If the axiom of choice holds (so that any cardinal number can be well-ordered), an infinite cardinal
is regular if and only if it cannot be expressed as the cardinal sum of a set of cardinality less than 
, the elements of which are cardinals less than 
.
An infinite ordinal
is regular if and only if
it is a limit ordinal which is not the limit of a set of smaller ordinals which set has order type
less than
. A regular ordinal is always an initial ordinal, though some initial ordinals are not regular.
Infinite well-ordered cardinals which are not regular are called singular cardinals. Finite cardinal numbers are typically not called regular or singular.
are finite. A finite sequence of finite ordinals always has a finite maximum, so 
cannot be the limit of any sequence of type less than 
whose elements are ordinals less than 
, and is therefore a regular ordinal.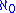 
(aleph-null) is a regular cardinal because its initial ordinal, 
, is regular. It can also be seen directly to be regular, as the cardinal sum of a finite number of finite cardinal numbers is itself finite.
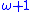is the next ordinal number
greater than
. It is singular, since it is not a limit ordinal. 
is the next limit ordinal after 
. It can be written as the limit of the sequence 
, 
, 
, 
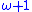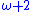, and so on. This sequence has order type 
, so 
is the limit of a sequence of type less than 
whose elements are ordinals less than 
, therefore it is singular.
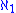is the next cardinal number
greater than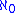
, so the cardinals less than 
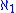are countable
(finite or denumerable). Assuming the axiom of choice, the union of a countable set of countable sets is itself countable. So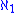
cannot be written as the sum of a countable set of countable cardinal numbers, and is regular.
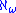is the next cardinal number after the sequence 
, 
, 
, 
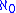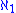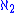, and so on. Its initial ordinal 
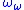is the limit of the sequence 
, 
, 
, 
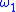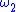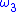, and so on, which has order type 
, so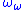 
is singular, and so is 
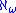. Assuming the axiom of choice, 
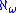is the first infinite cardinal which is singular (the first infinite ordinal which is singular is 
). Proving the existence of singular cardinals requires the axiom of replacement
, and in fact the inability to prove the existence of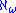
in Zermelo set theory
is what led Fraenkel to postulate this axiom.
s of the aleph function
, though not all fixed points are regular. For instance, the first fixed point is the limit of the
-sequence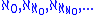 
and is therefore singular.
If the axiom of choice holds, then every successor cardinal is regular. Thus the regularity or singularity of most aleph numbers can be checked depending on whether the cardinal is a successor cardinal or a limit cardinal. Some cardinal numbers cannot be proven to be equal to any particular aleph, for instance the cardinality of the continuum
, whose value in ZFC may be any uncountable cardinal of uncountable cofinality (see Easton's theorem
). The continuum hypothesis
postulates that the cardinality of the continuum is equal to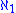
which is regular.
Without the axiom of choice, there would be cardinal numbers which were not well-orderable. Moreover, the cardinal sum of an arbitrary collection could not be defined. Therefore only the aleph number
s can meaningfully be called regular or singular cardinals. Furthermore, a successor aleph need not be regular. For instance, the union of a countable set of countable sets need not be countable. It is consistent with ZF
that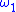
be the limit of a countable sequence of countable ordinals as well as the set of real numbers is countable union of countable sets. Furthermore, it is consistent with ZF that every aleph bigger than 
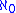is singular (a result proved by Moti Gitik
).
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, a regular cardinal is a cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
that is equal to its own cofinality
Cofinality
In mathematics, especially in order theory, the cofinality cf of a partially ordered set A is the least of the cardinalities of the cofinal subsets of A....
. So, crudely speaking, a regular cardinal is one which cannot be broken into a smaller collection of smaller parts.
(The situation is slightly more complicated in contexts where the axiom of choice might fail; in that case not all cardinals are necessarily the cardinalities of well-ordered sets. In that case, the above definition is restricted to well-orderable cardinals only.) If the axiom of choice holds (so that any cardinal number can be well-ordered), an infinite cardinal
is regular if and only if it cannot be expressed as the cardinal sum of a set of cardinality less than , the elements of which are cardinals less than .An infinite ordinal
is regular if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it is a limit ordinal which is not the limit of a set of smaller ordinals which set has order type
Order type
In mathematics, especially in set theory, two ordered sets X,Y are said to have the same order type just when they are order isomorphic, that is, when there exists a bijection f: X → Y such that both f and its inverse are monotone...
less than
. A regular ordinal is always an initial ordinal, though some initial ordinals are not regular.Infinite well-ordered cardinals which are not regular are called singular cardinals. Finite cardinal numbers are typically not called regular or singular.
Examples
The ordinals less than are finite. A finite sequence of finite ordinals always has a finite maximum, so cannot be the limit of any sequence of type less than whose elements are ordinals less than , and is therefore a regular ordinal. 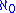(aleph-null) is a regular cardinal because its initial ordinal, , is regular. It can also be seen directly to be regular, as the cardinal sum of a finite number of finite cardinal numbers is itself finite.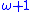 is the next ordinal numberSuccessor ordinal
In set theory, the successor of an ordinal number α is the smallest ordinal number greater than α. An ordinal number that is a successor is called a successor ordinal...
greater than
. It is singular, since it is not a limit ordinal. is the next limit ordinal after . It can be written as the limit of the sequence , , 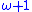, , 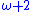and so on. This sequence has order type , so is the limit of a sequence of type less than whose elements are ordinals less than , therefore it is singular.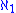 is the next cardinal numberSuccessor cardinal
In the theory of cardinal numbers, we can define a successor operation similar to that in the ordinal numbers. This coincides with the ordinal successor operation for finite cardinals, but in the infinite case they diverge because every infinite ordinal and its successor have the same cardinality...
greater than
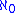, so the cardinals less than 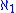are countableCountable set
In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
(finite or denumerable). Assuming the axiom of choice, the union of a countable set of countable sets is itself countable. So
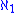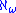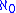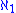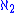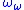cannot be written as the sum of a countable set of countable cardinal numbers, and is regular. is the next cardinal number after the sequence , , , , and so on. Its initial ordinal is the limit of the sequence , , 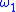, , 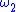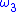and so on, which has order type , so 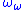is singular, and so is 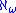. Assuming the axiom of choice, 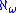is the first infinite cardinal which is singular (the first infinite ordinal which is singular is ). Proving the existence of singular cardinals requires the axiom of replacementAxiom schema of replacement
In set theory, the axiom schema of replacement is a schema of axioms in Zermelo–Fraenkel set theory that asserts that the image of any set under any definable mapping is also a set...
, and in fact the inability to prove the existence of
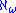in Zermelo set theoryZermelo set theory
Zermelo set theory, as set out in an important paper in 1908 by Ernst Zermelo, is the ancestor of modern set theory. It bears certain differences from its descendants, which are not always understood, and are frequently misquoted...
is what led Fraenkel to postulate this axiom.
Properties
Uncountable limit cardinals that are also regular are known as weakly inaccessible cardinals. They cannot be proved to exist within ZFC, though their existence is not known to be inconsistent with ZFC. Their existence is sometimes taken as an additional axiom. Inaccessible cardinals are necessarily fixed pointFixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
s of the aleph function
Aleph number
In set theory, a discipline within mathematics, the aleph numbers are a sequence of numbers used to represent the cardinality of infinite sets. They are named after the symbol used to denote them, the Hebrew letter aleph...
, though not all fixed points are regular. For instance, the first fixed point is the limit of the
-sequence 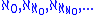and is therefore singular.If the axiom of choice holds, then every successor cardinal is regular. Thus the regularity or singularity of most aleph numbers can be checked depending on whether the cardinal is a successor cardinal or a limit cardinal. Some cardinal numbers cannot be proven to be equal to any particular aleph, for instance the cardinality of the continuum
Cardinality of the continuum
In set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....
, whose value in ZFC may be any uncountable cardinal of uncountable cofinality (see Easton's theorem
Easton's theorem
In set theory, Easton's theorem is a result on the possible cardinal numbers of powersets. showed via forcing that...
). The continuum hypothesis
Continuum hypothesis
In mathematics, the continuum hypothesis is a hypothesis, advanced by Georg Cantor in 1874, about the possible sizes of infinite sets. It states:Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems presented in the year 1900...
postulates that the cardinality of the continuum is equal to
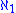which is regular.Without the axiom of choice, there would be cardinal numbers which were not well-orderable. Moreover, the cardinal sum of an arbitrary collection could not be defined. Therefore only the aleph number
Aleph number
In set theory, a discipline within mathematics, the aleph numbers are a sequence of numbers used to represent the cardinality of infinite sets. They are named after the symbol used to denote them, the Hebrew letter aleph...
s can meaningfully be called regular or singular cardinals. Furthermore, a successor aleph need not be regular. For instance, the union of a countable set of countable sets need not be countable. It is consistent with ZF
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
that
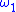be the limit of a countable sequence of countable ordinals as well as the set of real numbers is countable union of countable sets. Furthermore, it is consistent with ZF that every aleph bigger than 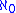is singular (a result proved by Moti GitikMoti Gitik
Moti Gitik is a mathematician, working in set theory. Gitik is professor at the Tel-Aviv University. He proved the consistency of "all uncountable cardinals are singular" from the consistency of "there is a proper class of strongly compact cardinals"...
).