
Wavefunction collapse
Encyclopedia
In quantum mechanics
, wave function collapse (also called collapse of the state vector or reduction of the wave packet) is the phenomenon in which a wave function—initially in a superposition
of several different possible eigenstates—appears to reduce to a single one of those states after interaction with an observer
. In simplified terms, it is the reduction of the physical possibilities into a single possibility as seen by an observer. It is one of two processes by which quantum systems evolve in time, according to the laws of quantum mechanics
as presented by John von Neumann
. The reality of wave function collapse has always been debatable, i.e., whether it is a fundamental physical phenomenon in its own right or just an epiphenomenon
of another process, such as quantum decoherence
. In recent decades the quantum decoherence view has gained popularity and is commonly taught at the graduate level (e.g. Cohen-Tannoudji
's standard textbook). Collapse may be understood as an update in a probabilistic model, given the observed result.
Hilbert space
). This can be expressed in Dirac or bra-ket notation
as a vector: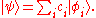
The kets , specify the different quantum "alternatives" available - a particular quantum state. Technically they form an orthonormal eigenvector basis
, specify the different quantum "alternatives" available - a particular quantum state. Technically they form an orthonormal eigenvector basis
, satisfying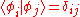 .
.
An observable - i.e. measurable parameter of the system is associated with each eigenbasis, with each quantum alternative having a specific value or eigenvalue, ei, of the observable. A "measurable parameter of the system" could be the usual position r, time t and momentum p of (say) a particle, but also its energy E, z-components of spin (sz), orbital (Lz) and total angular (Jz) momenta etc. In the basis representation these are respectivley .
.
The coefficients c1, c2, c3... are the probability amplitude
s corresponding to each basis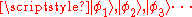 . These are complex numbers. The moduli square of ci, that is |ci|2 = ci*ci (* denotes complex conjugate
. These are complex numbers. The moduli square of ci, that is |ci|2 = ci*ci (* denotes complex conjugate
), is the probability of measuring the system to be in the state .
.
For simplicity in the following, all wave functions are assumed to be normalized; the total probability of measuring all possible states is unity:
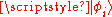 could appear in the measurement, the relative chances are given by the corresponding probabilities. When an external agency (an observer, experimenter) measures the observable associated with the eigenbasis
could appear in the measurement, the relative chances are given by the corresponding probabilities. When an external agency (an observer, experimenter) measures the observable associated with the eigenbasis 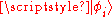 , the state of the wave function changes from the full
, the state of the wave function changes from the full  to only one of the basis states
to only one of the basis states 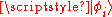 with Born probability |ci|2, that is:
with Born probability |ci|2, that is: .
.
All the other terms in the expansion of the wave function have vanished into nothing, hence the name "collapse". When the measurement is made - it yields an outcome, only one will occur, even though more than one could, so when it happens no measurement of the other states can subsequently be made.
If a more general measurement is made that detects the system in a state then the system makes a "jump" or quantum leap
then the system makes a "jump" or quantum leap
from the original state to the final state
to the final state  with probability of
with probability of 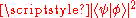 . Quantum leaps and wave function collapse are therefore merely two sides of the same coin.
. Quantum leaps and wave function collapse are therefore merely two sides of the same coin.
wrote his treatise Mathematische Grundlagen der Quantenmechanik in 1932, the phenomenon of "wave function collapse" was accommodated into the mathematical formulation of quantum mechanics
by postulating that there were two processes of wave function change:
In general, quantum systems exist in superpositions
of those basis states that most closely correspond to classical descriptions, and, when not being measured or observed, evolve according to the time dependent Schrödinger equation, relativistic quantum field theory or some form of quantum gravity
or string theory
, which is process (2) mentioned above. However, when the wave function collapses (process (1)), from an observer's perspective the state seems to "leap" or "jump" to just one of the basis states and uniquely acquire the value of the property being measured,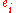 , associated with that particular basis state. After the collapse, the system begins to evolve again according to the Schrödinger equation or some equivalent wave equation.
, associated with that particular basis state. After the collapse, the system begins to evolve again according to the Schrödinger equation or some equivalent wave equation.
By explicitly dealing with the interaction of object and measuring instrument, von Neumann has attempted to create consistency of the two processes of wave function change.
He was able to prove the possibility of a quantum mechanical measurement scheme consistent with wave function collapse. However, he did not prove the necessity of such a collapse. Although von Neumann's projection postulate is often presented as a normative description of quantum measurement, it was conceived by taking into account experimental evidence available during the 1930s (in particular the Compton-Simon experiment has been paradigmatic), and many important present-day measurement procedures do not satisfy it (so-called measurements of the second kind).
The existence of the wave function collapse is required in
On the other hand, the collapse is considered as a redundant or optional approximation in
The cluster of phenomena described by the expression wave function collapse is a fundamental problem in the interpretation of quantum mechanics, and is known as the measurement problem
. The problem is not really confronted by the Copenhagen Interpretation, which postulates that this is a special characteristic of the "measurement" process. The Many-Worlds Interpretation deals with it by discarding the collapse-process, thus reformulating the relation between measurement apparatus and system in such a way that the linear laws of quantum mechanics are universally valid; that is, the only process according to which a quantum system evolves is governed by the Schrödinger equation or some relativistic
equivalent. Often tied in with the Many-Worlds Interpretation, but not limited to it, is the physical process of decoherence, which causes an apparent collapse. Decoherence is also important for the interpretation based on Consistent Histories.
A general description of the evolution of quantum mechanical systems is possible by using density operators
and quantum operation
s. In this formalism (which is closely related to the C*-algebraic formalism) the collapse of the wave function corresponds to a non-unitary quantum operation.
The significance ascribed to the wave function varies from interpretation to interpretation, and varies even within an interpretation (such as the Copenhagen Interpretation). If the wave function merely encodes an observer's knowledge of the universe then the wave function collapse corresponds to the receipt of new information. This is somewhat analogous to the situation in classical physics, except that the classical "wave function" does not necessarily obey a wave equation. If the wave function is physically real, in some sense and to some extent, then the collapse of the wave function is also seen as a real process, to the same extent.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, wave function collapse (also called collapse of the state vector or reduction of the wave packet) is the phenomenon in which a wave function—initially in a superposition
Quantum superposition
Quantum superposition is a fundamental principle of quantum mechanics. It holds that a physical system exists in all its particular, theoretically possible states simultaneously; but, when measured, it gives a result corresponding to only one of the possible configurations.Mathematically, it...
of several different possible eigenstates—appears to reduce to a single one of those states after interaction with an observer
Observer effect (physics)
In physics, the term observer effect refers to changes that the act of observation will make on the phenomenon being observed. This is often the result of instruments that, by necessity, alter the state of what they measure in some manner...
. In simplified terms, it is the reduction of the physical possibilities into a single possibility as seen by an observer. It is one of two processes by which quantum systems evolve in time, according to the laws of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
as presented by John von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
. The reality of wave function collapse has always been debatable, i.e., whether it is a fundamental physical phenomenon in its own right or just an epiphenomenon
Epiphenomenon
An epiphenomenon is a secondary phenomenon that occurs alongside or in parallel to a primary phenomenon.-Medicine:...
of another process, such as quantum decoherence
Quantum decoherence
In quantum mechanics, quantum decoherence is the loss of coherence or ordering of the phase angles between the components of a system in a quantum superposition. A consequence of this dephasing leads to classical or probabilistically additive behavior...
. In recent decades the quantum decoherence view has gained popularity and is commonly taught at the graduate level (e.g. Cohen-Tannoudji
Claude Cohen-Tannoudji
Claude Cohen-Tannoudji is a French physicist and Nobel Laureate. He shared the 1997 Nobel Prize in Physics with Steven Chu and William Daniel Phillips for research in methods of laser cooling and trapping atoms...
's standard textbook). Collapse may be understood as an update in a probabilistic model, given the observed result.
Mathematical description
It is quite simple to describe this phenomenon mathematically - and this leads to the curious philosophical implications and difficulty in understanding what the wave function means.Mathematical background
The quantum state of a physical system is described by a wave function (in turn - an element of a projectiveProjective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
). This can be expressed in Dirac or bra-ket notation
Bra-ket notation
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
as a vector:
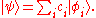
The kets
 , specify the different quantum "alternatives" available - a particular quantum state. Technically they form an orthonormal eigenvector basis
, specify the different quantum "alternatives" available - a particular quantum state. Technically they form an orthonormal eigenvector basisBasis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
, satisfying
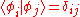 .
.An observable - i.e. measurable parameter of the system is associated with each eigenbasis, with each quantum alternative having a specific value or eigenvalue, ei, of the observable. A "measurable parameter of the system" could be the usual position r, time t and momentum p of (say) a particle, but also its energy E, z-components of spin (sz), orbital (Lz) and total angular (Jz) momenta etc. In the basis representation these are respectivley
 .
.The coefficients c1, c2, c3... are the probability amplitude
Probability amplitude
In quantum mechanics, a probability amplitude is a complex number whose modulus squared represents a probability or probability density.For example, if the probability amplitude of a quantum state is \alpha, the probability of measuring that state is |\alpha|^2...
s corresponding to each basis
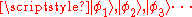 . These are complex numbers. The moduli square of ci, that is |ci|2 = ci*ci (* denotes complex conjugate
. These are complex numbers. The moduli square of ci, that is |ci|2 = ci*ci (* denotes complex conjugateComplex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
), is the probability of measuring the system to be in the state
 .
.For simplicity in the following, all wave functions are assumed to be normalized; the total probability of measuring all possible states is unity:

The process of collapse
With these definitions it is easy to describe the process of collapse. Initially - there are a range of possible outcomes for measurement of the system, any one of the basis states of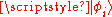 could appear in the measurement, the relative chances are given by the corresponding probabilities. When an external agency (an observer, experimenter) measures the observable associated with the eigenbasis
could appear in the measurement, the relative chances are given by the corresponding probabilities. When an external agency (an observer, experimenter) measures the observable associated with the eigenbasis 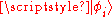 , the state of the wave function changes from the full
, the state of the wave function changes from the full  to only one of the basis states
to only one of the basis states 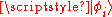 with Born probability |ci|2, that is:
with Born probability |ci|2, that is: .
.All the other terms in the expansion of the wave function have vanished into nothing, hence the name "collapse". When the measurement is made - it yields an outcome, only one will occur, even though more than one could, so when it happens no measurement of the other states can subsequently be made.
If a more general measurement is made that detects the system in a state
 then the system makes a "jump" or quantum leap
then the system makes a "jump" or quantum leapQuantum leap
In physics and chemistry, an atomic electron transition is a change of an electron from one quantum state to another within an atom...
from the original state
 to the final state
to the final state  with probability of
with probability of 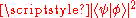 . Quantum leaps and wave function collapse are therefore merely two sides of the same coin.
. Quantum leaps and wave function collapse are therefore merely two sides of the same coin.History and context
By the time John von NeumannJohn von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
wrote his treatise Mathematische Grundlagen der Quantenmechanik in 1932, the phenomenon of "wave function collapse" was accommodated into the mathematical formulation of quantum mechanics
Mathematical formulation of quantum mechanics
The mathematical formulations of quantum mechanics are those mathematical formalisms that permit a rigorous description of quantum mechanics. Such are distinguished from mathematical formalisms for theories developed prior to the early 1900s by the use of abstract mathematical structures, such as...
by postulating that there were two processes of wave function change:
- The probabilisticProbabilityProbability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
, non-unitaryUnitary transformationIn mathematics, a unitary transformation may be informally defined as a transformation that respects the inner product: the inner product of two vectors before the transformation is equal to their inner product after the transformation....
, non-local, discontinuous change brought about by observation and measurement, as outlined above. - The deterministic, unitary, continuous time evolutionTime evolutionTime evolution is the change of state brought about by the passage of time, applicable to systems with internal state . In this formulation, time is not required to be a continuous parameter, but may be discrete or even finite. In classical physics, time evolution of a collection of rigid bodies...
of an isolated system that obeys Schrödinger's equation (or nowadays some relativistic, local equivalent, i.e. Dirac's equation).
In general, quantum systems exist in superpositions
Quantum superposition
Quantum superposition is a fundamental principle of quantum mechanics. It holds that a physical system exists in all its particular, theoretically possible states simultaneously; but, when measured, it gives a result corresponding to only one of the possible configurations.Mathematically, it...
of those basis states that most closely correspond to classical descriptions, and, when not being measured or observed, evolve according to the time dependent Schrödinger equation, relativistic quantum field theory or some form of quantum gravity
Quantum gravity
Quantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
or string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
, which is process (2) mentioned above. However, when the wave function collapses (process (1)), from an observer's perspective the state seems to "leap" or "jump" to just one of the basis states and uniquely acquire the value of the property being measured,
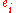 , associated with that particular basis state. After the collapse, the system begins to evolve again according to the Schrödinger equation or some equivalent wave equation.
, associated with that particular basis state. After the collapse, the system begins to evolve again according to the Schrödinger equation or some equivalent wave equation.By explicitly dealing with the interaction of object and measuring instrument, von Neumann has attempted to create consistency of the two processes of wave function change.
He was able to prove the possibility of a quantum mechanical measurement scheme consistent with wave function collapse. However, he did not prove the necessity of such a collapse. Although von Neumann's projection postulate is often presented as a normative description of quantum measurement, it was conceived by taking into account experimental evidence available during the 1930s (in particular the Compton-Simon experiment has been paradigmatic), and many important present-day measurement procedures do not satisfy it (so-called measurements of the second kind).
The existence of the wave function collapse is required in
- the Copenhagen interpretationCopenhagen interpretationThe Copenhagen interpretation is one of the earliest and most commonly taught interpretations of quantum mechanics. It holds that quantum mechanics does not yield a description of an objective reality but deals only with probabilities of observing, or measuring, various aspects of energy quanta,...
- the objective collapse interpretations
- the transactional interpretationTransactional interpretationThe transactional interpretation of quantum mechanics describes quantum interactions in terms of a standing wave formed by retarded and advanced waves. It was first proposed in 1986 by John G...
- the von Neumann interpretation in which consciousness causes collapse.
On the other hand, the collapse is considered as a redundant or optional approximation in
- the Bohm interpretationBohm interpretationThe de Broglie–Bohm theory, also called the pilot-wave theory, Bohmian mechanics, and the causal interpretation, is an interpretation of quantum theory. In addition to a wavefunction on the space of all possible configurations, it also includes an actual configuration, even in situations where...
- the Ensemble InterpretationEnsemble InterpretationThe ensemble interpretation, or statistical interpretation of quantum mechanics, is an interpretation that can be viewed as a minimalist interpretation; it is a quantum mechanical interpretation that claims to make the fewest assumptions associated with the standard mathematical formalization...
- the Many-Worlds InterpretationMany-worlds interpretationThe many-worlds interpretation is an interpretation of quantum mechanics that asserts the objective reality of the universal wavefunction, but denies the actuality of wavefunction collapse. Many-worlds implies that all possible alternative histories and futures are real, each representing an...
- interpretations based on Consistent HistoriesConsistent historiesIn quantum mechanics, the consistent histories approach is intended to give a modern interpretation of quantum mechanics, generalising the conventional Copenhagen interpretation and providing a natural interpretation of quantum cosmology...
The cluster of phenomena described by the expression wave function collapse is a fundamental problem in the interpretation of quantum mechanics, and is known as the measurement problem
Measurement problem
The measurement problem in quantum mechanics is the unresolved problem of how wavefunction collapse occurs. The inability to observe this process directly has given rise to different interpretations of quantum mechanics, and poses a key set of questions that each interpretation must answer...
. The problem is not really confronted by the Copenhagen Interpretation, which postulates that this is a special characteristic of the "measurement" process. The Many-Worlds Interpretation deals with it by discarding the collapse-process, thus reformulating the relation between measurement apparatus and system in such a way that the linear laws of quantum mechanics are universally valid; that is, the only process according to which a quantum system evolves is governed by the Schrödinger equation or some relativistic
Theory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
equivalent. Often tied in with the Many-Worlds Interpretation, but not limited to it, is the physical process of decoherence, which causes an apparent collapse. Decoherence is also important for the interpretation based on Consistent Histories.
A general description of the evolution of quantum mechanical systems is possible by using density operators
Density matrix
In quantum mechanics, a density matrix is a self-adjoint positive-semidefinite matrix of trace one, that describes the statistical state of a quantum system...
and quantum operation
Quantum operation
In quantum mechanics, a quantum operation is a mathematical formalism used to describe a broad class of transformations that a quantum mechanical system can undergo. This was first discussed as a general stochastic transformation for a density matrix by George Sudarshan...
s. In this formalism (which is closely related to the C*-algebraic formalism) the collapse of the wave function corresponds to a non-unitary quantum operation.
The significance ascribed to the wave function varies from interpretation to interpretation, and varies even within an interpretation (such as the Copenhagen Interpretation). If the wave function merely encodes an observer's knowledge of the universe then the wave function collapse corresponds to the receipt of new information. This is somewhat analogous to the situation in classical physics, except that the classical "wave function" does not necessarily obey a wave equation. If the wave function is physically real, in some sense and to some extent, then the collapse of the wave function is also seen as a real process, to the same extent.
See also
- Arrow of timeArrow of timeThe arrow of time, or time’s arrow, is a term coined in 1927 by the British astronomer Arthur Eddington to describe the "one-way direction" or "asymmetry" of time...
- Interpretation of quantum mechanicsInterpretation of quantum mechanicsAn interpretation of quantum mechanics is a set of statements which attempt to explain how quantum mechanics informs our understanding of nature. Although quantum mechanics has held up to rigorous and thorough experimental testing, many of these experiments are open to different interpretations...
- Quantum decoherenceQuantum decoherenceIn quantum mechanics, quantum decoherence is the loss of coherence or ordering of the phase angles between the components of a system in a quantum superposition. A consequence of this dephasing leads to classical or probabilistically additive behavior...
- Quantum interference
- Schrödinger's catSchrödinger's catSchrödinger's cat is a thought experiment, usually described as a paradox, devised by Austrian physicist Erwin Schrödinger in 1935. It illustrates what he saw as the problem of the Copenhagen interpretation of quantum mechanics applied to everyday objects. The scenario presents a cat that might be...
- Zeno effect

