Quantum superposition
Encyclopedia
Quantum superposition is a fundamental principle of quantum mechanics
. It holds that a physical system (say, an electron) exists in all its particular, theoretically possible states (or, configuration of its properties) simultaneously; but, when measured, it gives a result corresponding to only one of the possible configurations.
Mathematically, it refers to a property of solutions to the Schrödinger equation
; since the Schrödinger equation
is linear
, any linear combination of solutions to a particular equation will also be a solution of it. Such solutions are often made to be orthogonal (i.e. the vectors are at right-angles to each other), such as the energy levels of an electron
. By doing so the overlap energy of the states is nullified, and the expectation value of an operator
(any superposition
state) is the expectation value of the operator in the individual states, multiplied by the fraction of the superposition state that is "in" that state.
An example of a directly observable effect of superposition is interference peaks from an electron
wave
in a double-slit experiment
.
The principle was described by Paul Dirac
as follows:
Similarly, probability theory
states that the probability of an event can be described by a combination of the probabilities of certain specific other events (see Mathematical treatment
). For example, the probability of flipping two coins (coin A and coin B) and having at least one land head-up can be expressed as the sum of the probabilities for three specific events: coin A heads with B tails, coin A heads with B heads, and coin A tails with B heads. In this case the probability could be expressed as:
or even:
Probability theory, as with quantum theory, would also require that the sum of the probabilities for all possible events, not just those satisfying the condition, be equal to unity (i.e. to one hundred percent). Thus:
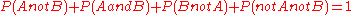
Probability theory also states that the probability distribution along a continuum (i.e. the chance of an object being in a particular position along a continuous set of coordinates) or among discrete events (the example above) can be described using a probability density
or unit vector, respectively, with the probability magnitude being a square of the density function.
In quantum mechanics an additional layer of analysis is introduced, since the probability density function
is now more specifically a wave function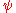
. The wave function is either a complex function of a finite set of real variables or a complex vector formed of a finite or infinite number of components. As the coefficients in the linear combination that describes our probability density
are now complex, the probability must now come from the absolute value of the multiplication of the wave function by its complex conjugate
. In cases where the functions are not complex, the probability of an event occurring which is dependent upon any one of all possible events in a subset occurring is the simple sum of the event probabilities in that subset. For example, if an observer rings a bell whenever one or more coins land heads up in the example above, then the probability of the observer ringing a bell is the same as the sum of the probabilities of each event in which at least one coin lands heads up. This is a simple sum because the square of the probability function is always positive. Using the wave equation, the outcome of multiplication of the function by its complex conjugate (i.e. the result of squaring it) is not always positive, hence may produce counter-intuitive results.
For example, if a photon
in a plus spin
state has a 0.1 amplitude to be absorbed and take an atom to the second energy level, and if the photon in a minus spin state has a −0.1 amplitude to do the same, a photon which has an equal amplitude to be plus or minus would have zero amplitude to take the atom to the second excited state and the atom will not be excited. If the photon's spin is measured before it reaches the atom, whatever the answer - plus or minus - it will have a non zero amplitude to excite the atom, plus or minus 0.1.
Assuming normalization (i.e. that all probabilities in the set do total 100%), the probability density in quantum mechanics is equal to the square of the absolute value of the amplitude of the waveform. The further the amplitude is from zero, the bigger the probability. Where probability distribution is represented as a continuous function, the probability is the integral of the density function over the relevant values. Where the wave equation is represented as a complex vector, the probability will be extracted from the absolute value of an inner-product of the coefficient matrix and its complex conjugate. In the atom example above, the probability that the atom will be excited is zero. But the only occasion on which probability enters the picture is if an observer looks to see which way the atom goes; then the different amplitudes become probabilities for seeing different things. So if you check to see whether the atom has been excited to the second energy level immediately after the photon with zero amplitude reaches it, there is no chance of seeing the atom excited.
Another example: If a particle can be in position A and position B, it can also be in a state where it is an amount "3i/5" in position A and an amount "4/5" in position B. To write this, physicists usually say:
In the description, only the relative size of the different components matter, and their angle to each other on the complex plane. This is usually stated by declaring that two states which are a multiple of one another are the same as far as the description of the situation is concerned.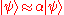
The fundamental law of quantum mechanics is that the evolution is linear
, meaning that if state A turns into A' and B turns into B' after 10 seconds, then after 10 seconds the superposition
turns into a mixture of A' and B' with the same coefficients as A and B.
A particle can have any position, so that there are different states which have any value of the position x. These are written:
The principle of superposition guarantees that there are states which are arbitrary superpositions of all the positions with complex coefficients:
This sum is defined only if the index
is discrete. If the index is over 
, then the sum is not defined and is replaced by an integral instead. The quantity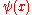 
is called the wavefunction
of the particle.
If a particle can have some discrete orientations of the spin, say the spin can be aligned with the z axis
or against it 
, then the particle can have any state of the form:
If the particle has both position and spin, the state is a superposition of all possibilities for both:
The configuration space of a quantum mechanical system cannot be worked out without some physical knowledge. The input is usually the allowed different classical configurations, but without the duplication of including both position and momentum.
A pair of particles can be in any combination of pairs of positions. A state where one particle is at position x and the other is at position y is written
. The most general state is a superposition of the possibilities:
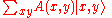
The description of the two particles is much larger than the description of one particle — it is a function in twice the number of dimensions. This is also true in probability, when the statistics of two random things are correlated. If two particles are uncorrelated, the probability distribution for their joint position P(x,y) is a product of the probability of finding one at one position and the other at the other position: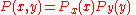
In quantum mechanics, two particles can be in special states where the amplitudes of their position are uncorrelated. For quantum amplitudes, the word entanglement
replaces the word correlation, but the analogy is exact. A disentangled wavefunction has the form:
while an entangled wavefunction does not have this form. Like correlation in probability, there are many more entangled states than disentangled ones. For instance, when two particles which start out with an equal probability to be anywhere in a box have a strong attraction and a way to dissipate energy, they can easily come together to make a bound state. The bound state still has an equal probability to be anywhere, so that each particle is still equally likely to be anywhere, but the two particles are now entangled: so wherever one particle is, the other is too.
there is a similar principle. If a system has a probabilistic description, this description gives the probability of any configuration, and given any two different configurations, there is a state which is partly this and partly that, with positive real number coefficients, the probabilities, which say how much of each there is.
For example, if we have a probability distribution for where a particle is, it is described by the "state"
Where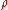
is the probability density
function, a positive number that measures the probability that the particle will be found at a certain location.
The evolution equation is also linear in probability, for fundamental reasons. If the particle has some probability for going from position x to y, and from z to y, the probability of going to y starting from a state which is half-x and half-z is a half-and-half mixture of the probability of going to y from each of the options. This is the principle of linear superposition in probability.
Quantum mechanics is different, because the numbers can be positive or negative. While the complex nature of the numbers is just a doubling, if you consider the real and imaginary parts separately, the sign of the coefficients is important. In probability, two different possible outcomes always add together, so that if there are more options to get to a point z, the probability always goes up. In quantum mechanics, different possibilities can cancel.
In probability theory with a finite number of states, the probabilities can always be multiplied by a positive number to make their sum equal to one. For example, if there is a three state probability system: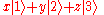
where the probabilities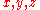
are positive numbers. Rescaling x,y,z so that
The geometry of the state space is a revealed to be a triangle. In general it is a simplex
. There are special points in a triangle or simplex corresponding to the corners, and these points are those where one of the probabilities is equal to 1 and the others are zero. These are the unique locations where the position is known with certainty.
In a quantum mechanical system with three states, the quantum mechanical wavefunction is a superposition of states again, but this time twice as many quantities with no restriction on the sign: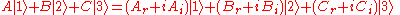
rescaling the variables so that the sum of the squares is 1, the geometry of the space is revealed to be a high dimensional sphere
.
A sphere has a large amount of symmetry, it can be viewed in different coordinate systems or bases
. So unlike a probability theory, a quantum theory has a large number of different bases in which it can be equally well described. The geometry of the phase space can be viewed as a hint that the quantity in quantum mechanics which corresponds to the probability is the absolute square of the coefficient of the superposition.
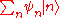
So that the infinite list of amplitudes
completely describes the quantum state of the particle. This list is called the state vector, and formally it is an element of a Hilbert space
, an infinite dimensional complex vector space
. It is usual to represent the state so that the sum of the absolute squares of the amplitudes add up to one: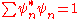
For a particle described by probability theory random walking on a line, the analogous thing is the list of probabilities
, which give the probability of any position. The quantities that describe how they change in time are the transition probabilities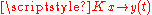 
, which gives the probability that, starting at x, the particle ends up at y after time t. The total probability of ending up at y is given by the sum over all the possibilities
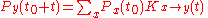
The condition of conservation of probability states that starting at any x, the total probability to end up somewhere must add up to 1:
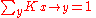
So that the total probability will be preserved, K is what is called a stochastic matrix
.
When no time passes, nothing changes: for zero elapsed time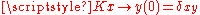
, the K matrix is zero except from a state to itself. So in the case that the time is short, it is better to talk about the rate of change of the probability instead of the absolute change in the probability.
where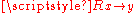
is the time derivative of the K matrix:
.
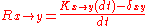The equation for the probabilities is a differential equation which is sometimes called the master equation:
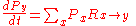
The R matrix is the probability per unit time for the particle to make a transition from x to y. The condition that the K matrix elements add up to one becomes the condition that the R matrix elements add up to zero:
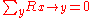
One simple case to study is when the R matrix has an equal probability to go one unit to the left or to the right, describing a particle which has a constant rate of random walking. In this case
is zero unless y is either x+1,x, or x−1, when y is x+1 or x−1, the R matrix has value c, and in order for the sum of the R matrix coefficients to equal zero, the value of 
must be −2c. So the probabilities obey the discretized diffusion equation:
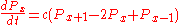
which, when c is scaled appropriately and the P distribution is smooth enough to think of the system in a continuum limit becomes:
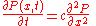
Which is the diffusion equation.
Quantum amplitudes give the rate at which amplitudes change in time, and they are mathematically exactly the same except that they are complex numbers. The analog of the finite time K matrix is called the U matrix:
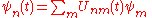
Since the sum of the absolute squares of the amplitudes must be constant,
must be unitary:
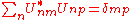
or, in matrix notation,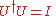
The rate of change of U is called the Hamiltonian
H, up to a traditional factor of i:
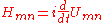
The Hamiltonian gives the rate at which the particle has an amplitude to go from m to n. The reason it is multiplied by i is that the condition that U is unitary translates to the condition:
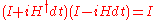
which says that H is Hermitian
. The eigenvalues of the Hermitian matrix H are real quantities which have a physical interpretation as energy levels. If the factor i were absent, the H matrix would be antihermitian and would have purely imaginary eigenvalues, which is not the traditional way quantum mechanics represents observable quantities like the energy.
For a particle which has equal amplitude to move left and right, the Hermitian matrix H is zero except for nearest neighbors, where it has the value c. If the coefficient is everywhere constant, the condition that H is Hermitian demands that the amplitude to move to the left is the complex conjugate of the amplitude to move to the right. The equation of motion for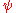
is the time differential equation:
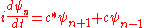
In the case that left and right are symmetric, c is real. By redefining the phase of the wavefunction in time,
, the amplitudes for being at different locations are only rescaled, so that the physical situation is unchanged. But this phase rotation introduces a linear term.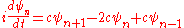
which is the right choice of phase to take the continuum limit. When c is very large and psi is slowly varying so that the lattice can be thought of as a line, this becomes the free Schrödinger equation
:
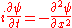
If there is an additional term in the H matrix which is an extra phase rotation which varies from point to point, the continuum limit is the Schrödinger equation with a potential energy: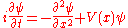
These equations describe the motion of a single particle in non-relativistic quantum mechanics.
, the probability to go between two points after a finite number of time steps can be represented as a sum over all paths of the probability of taking each path:
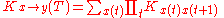
where the sum extends over all paths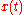
with the property that 
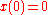and 
. The analogous expression in quantum mechanics is the path integral
.
A generic transition matrix in probability has a stationary distribution, which is the eventual probability to be found at any point no matter what the starting point. If there is a nonzero probability for any two paths to reach the same point at the same time, this stationary distribution does not depend on the initial conditions. In probability theory, the probability m for the stochastic matrix obeys detailed balance
when the stationary distribution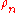
has the property:
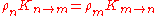
Detailed balance says that the total probability of going from m to n in the stationary distribution, which is the probability of starting at m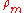
times the probability of hopping from m to n, is equal to the probability of going from n to m, so that the total back-and-forth flow of probability in equilibrium is zero along any hop. The condition is automatically satisfied when n=m, so it has the same form when written as a condition for the transition-probability R matrix.
When the R matrix obeys detailed balance, the scale of the probabilities can be redefined using the stationary distribution so that they no longer sum to 1:
In the new coordinates, the R matrix is rescaled as follows:
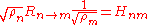
and H is symmetric
This matrix H defines a quantum mechanical system:
whose Hamiltonian has the same eigenvalues as those of the R matrix of the statistical system. The eigenvectors are the same too, except expressed in the rescaled basis. The stationary distribution of the statistical system is the ground state of the Hamiltonian and it has energy exactly zero, while all the other energies are positive. If H is exponentiated to find the U matrix:
and t is allowed to take on complex values, the K' matrix is found by taking time imaginary.
For quantum systems which are invariant under time reversal
the Hamiltonian can be made real and symmetric, so that the action of time-reversal on the wave-function is just complex conjugation. If such a Hamiltonian has a unique lowest energy state with a positive real wave-function, as it often does for physical reasons, it is connected to a stochastic system in imaginary time. This relationship between stochastic systems and quantum systems sheds much light on supersymmetry
.
In quantum computing the phrase "cat state" often refers to the special entanglement of qubit
s wherein the qubits are in an equal superposition of all being 0 and all being 1; i.e.,
.
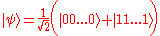to a quantum mechanical particle, the configurations of the particle are all positions, so the superpositions make a complex wave in space. The coefficients of the linear superposition are a wave which describes the particle as best as is possible, and whose amplitude interferes according to the Huygens principle.
For any physical property in quantum mechanics
, there is a list of all the states where that property has some value. These states are necessarily perpendicular to each other using the Euclidean notion of perpendicularity which comes from sums-of-squares length, except that they also must not be i multiples of each other. This list of perpendicular states has an associated value which is the value of the physical property. The superposition principle guarantees that any state can be written as a combination of states of this form with complex coefficients.
Write each state with the value q of the physical quantity as a vector in some basis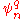
, a list of numbers at each value of n for the vector which has value q for the physical quantity. Now form the outer product of the vectors by multiplying all the vector components and add them with coefficients to make the matrix
where the sum extends over all possible values of q. This matrix is necessarily symmetric because it is formed from the orthogonal states, and has eigenvalues q. The matrix A is called the observable associated to the physical quantity. It has the property that the eigenvalues and eigenvectors determine the physical quantity and the states which have definite values for this quantity.
Every physical quantity has a Hermitian linear operator associated to it, and the states where the value of this physical quantity is definite are the eigenstates of this linear operator. The linear combination of two or more eigenstates results in quantum superposition of two or more values of the quantity. If the quantity is measured, the value of the physical quantity will be random, with a probability equal to the square of the coefficient of the superposition in the linear combination. Immediately after the measurement, the state will be given by the eigenvector corresponding to the measured eigenvalue.
It is natural to ask why "real" (macroscopic, Newtonian) objects and events do not seem to display quantum mechanical features such as superposition. In 1935, Erwin Schrödinger
devised a well-known thought experiment, now known as Schrödinger's cat
, which highlighted the dissonance between quantum mechanics and Newtonian physics, where only one configuration occurs, although a configuration for a particle in Newtonian physics specifies both position and momentum.
In fact, quantum superposition results in many directly observable effects, such as interference peaks from an electron
wave
in a double-slit experiment
. The superpositions, however, persist at all scales, absent a mechanism for removing them. This mechanism can be philosophical as in the Copenhagen interpretation
, or physical.
Recent research indicates that chlorophyll
within plants appears to exploit the feature of quantum superposition to achieve greater efficiency in transporting energy, allowing pigment proteins to be spaced further apart than would otherwise be possible.
If the operators corresponding to two observables do not commute
, they have no simultaneous eigenstates and they obey an uncertainty principle
. A state where one observable has a definite value corresponds to a superposition of many states for the other observable.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. It holds that a physical system (say, an electron) exists in all its particular, theoretically possible states (or, configuration of its properties) simultaneously; but, when measured, it gives a result corresponding to only one of the possible configurations.
Mathematically, it refers to a property of solutions to the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
; since the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
is linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
, any linear combination of solutions to a particular equation will also be a solution of it. Such solutions are often made to be orthogonal (i.e. the vectors are at right-angles to each other), such as the energy levels of an electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
. By doing so the overlap energy of the states is nullified, and the expectation value of an operator
Operator (physics)
In physics, an operator is a function acting on the space of physical states. As a resultof its application on a physical state, another physical state is obtained, very often along withsome extra relevant information....
(any superposition
Superposition
Superposition can refer to:* The superposition principle in physics, mathematics, and engineering, describes the overlapping of waves. Particular applications include :** Quantum superposition, in quantum physics** Superposition theorem, in electronics....
state) is the expectation value of the operator in the individual states, multiplied by the fraction of the superposition state that is "in" that state.
An example of a directly observable effect of superposition is interference peaks from an electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
wave
Wave
In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
in a double-slit experiment
Double-slit experiment
The double-slit experiment, sometimes called Young's experiment, is a demonstration that matter and energy can display characteristics of both waves and particles...
.
Concept
The principle of quantum superposition states that if a physical system may be in some configuration—an arrangement of particles or fields—and if the system could also be in another configuration, then it is in a state which is a superposition of the two, where the amount of each configuration that is in the superposition is specified by a complex number.The principle was described by Paul Dirac
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
as follows:
The general principle of superposition of quantum mechanics applies to the states [that are theoretically possible without mutual interference or contradiction] ... of any one dynamical system. It requires us to assume that between these states there exist peculiar relationships such that whenever the system is definitely in one state we can consider it as being partly in each of two or more other states. The original state must be regarded as the result of a kind of superposition of the two or more new states, in a way that cannot be conceived on classical ideas. Any state may be considered as the result of a superposition of two or more other states, and indeed in an infinite number of ways. Conversely any two or more states may be superposed to give a new state...
The non-classical nature of the superposition process is brought out clearly if we consider the superposition of two states, A and B, such that there exists an observation which, when made on the system in state A, is certain to lead to one particular result, a say, and when made on the system in state B is certain to lead to some different result, b say. What will be the result of the observation when made on the system in the superposed state? The answer is that the result will be sometimes a and sometimes b, according to a probability law depending on the relative weights of A and B in the superposition process. It will never be different from both a and b. The intermediate character of the state formed by superposition thus expresses itself through the probability of a particular result for an observation being intermediate between the corresponding probabilities for the original states, not through the result itself being intermediate between the corresponding results for the original states.
Examples
For an equation describing a physical phenomenon, the superposition principle states that a combination of solutions to a linear equation is also a solution of it. When this is true the equation is said to obey the superposition principle. Thus if functions f1, f2 and f3 each solve the linear equation ψ, then ψ=c1f1+c2f2+c3f3 would also be a solution, in which each c is a coefficient. For example, the electrical field due to a distribution of charged particles can be described by the sum of the contributions of the individual particles.Similarly, probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
states that the probability of an event can be described by a combination of the probabilities of certain specific other events (see Mathematical treatment
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
). For example, the probability of flipping two coins (coin A and coin B) and having at least one land head-up can be expressed as the sum of the probabilities for three specific events: coin A heads with B tails, coin A heads with B heads, and coin A tails with B heads. In this case the probability could be expressed as:
or even:
Probability theory, as with quantum theory, would also require that the sum of the probabilities for all possible events, not just those satisfying the condition, be equal to unity (i.e. to one hundred percent). Thus:
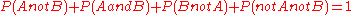
Probability theory also states that the probability distribution along a continuum (i.e. the chance of an object being in a particular position along a continuous set of coordinates) or among discrete events (the example above) can be described using a probability density
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
or unit vector, respectively, with the probability magnitude being a square of the density function.
In quantum mechanics an additional layer of analysis is introduced, since the probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
is now more specifically a wave function
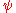. The wave function is either a complex function of a finite set of real variables or a complex vector formed of a finite or infinite number of components. As the coefficients in the linear combination that describes our probability densityProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
are now complex, the probability must now come from the absolute value of the multiplication of the wave function by its complex conjugate
. In cases where the functions are not complex, the probability of an event occurring which is dependent upon any one of all possible events in a subset occurring is the simple sum of the event probabilities in that subset. For example, if an observer rings a bell whenever one or more coins land heads up in the example above, then the probability of the observer ringing a bell is the same as the sum of the probabilities of each event in which at least one coin lands heads up. This is a simple sum because the square of the probability function is always positive. Using the wave equation, the outcome of multiplication of the function by its complex conjugate (i.e. the result of squaring it) is not always positive, hence may produce counter-intuitive results.For example, if a photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
in a plus spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
state has a 0.1 amplitude to be absorbed and take an atom to the second energy level, and if the photon in a minus spin state has a −0.1 amplitude to do the same, a photon which has an equal amplitude to be plus or minus would have zero amplitude to take the atom to the second excited state and the atom will not be excited. If the photon's spin is measured before it reaches the atom, whatever the answer - plus or minus - it will have a non zero amplitude to excite the atom, plus or minus 0.1.
Assuming normalization (i.e. that all probabilities in the set do total 100%), the probability density in quantum mechanics is equal to the square of the absolute value of the amplitude of the waveform. The further the amplitude is from zero, the bigger the probability. Where probability distribution is represented as a continuous function, the probability is the integral of the density function over the relevant values. Where the wave equation is represented as a complex vector, the probability will be extracted from the absolute value of an inner-product of the coefficient matrix and its complex conjugate. In the atom example above, the probability that the atom will be excited is zero. But the only occasion on which probability enters the picture is if an observer looks to see which way the atom goes; then the different amplitudes become probabilities for seeing different things. So if you check to see whether the atom has been excited to the second energy level immediately after the photon with zero amplitude reaches it, there is no chance of seeing the atom excited.
Another example: If a particle can be in position A and position B, it can also be in a state where it is an amount "3i/5" in position A and an amount "4/5" in position B. To write this, physicists usually say:
In the description, only the relative size of the different components matter, and their angle to each other on the complex plane. This is usually stated by declaring that two states which are a multiple of one another are the same as far as the description of the situation is concerned.
The fundamental law of quantum mechanics is that the evolution is linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
, meaning that if state A turns into A' and B turns into B' after 10 seconds, then after 10 seconds the superposition
turns into a mixture of A' and B' with the same coefficients as A and B.A particle can have any position, so that there are different states which have any value of the position x. These are written:
The principle of superposition guarantees that there are states which are arbitrary superpositions of all the positions with complex coefficients:
This sum is defined only if the index
is discrete. If the index is over , then the sum is not defined and is replaced by an integral instead. The quantity 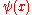is called the wavefunctionWavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
of the particle.
If a particle can have some discrete orientations of the spin, say the spin can be aligned with the z axis
or against it , then the particle can have any state of the form:If the particle has both position and spin, the state is a superposition of all possibilities for both:
The configuration space of a quantum mechanical system cannot be worked out without some physical knowledge. The input is usually the allowed different classical configurations, but without the duplication of including both position and momentum.
A pair of particles can be in any combination of pairs of positions. A state where one particle is at position x and the other is at position y is written
. The most general state is a superposition of the possibilities: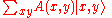The description of the two particles is much larger than the description of one particle — it is a function in twice the number of dimensions. This is also true in probability, when the statistics of two random things are correlated. If two particles are uncorrelated, the probability distribution for their joint position P(x,y) is a product of the probability of finding one at one position and the other at the other position:
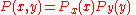
In quantum mechanics, two particles can be in special states where the amplitudes of their position are uncorrelated. For quantum amplitudes, the word entanglement
Quantum entanglement
Quantum entanglement occurs when electrons, molecules even as large as "buckyballs", photons, etc., interact physically and then become separated; the type of interaction is such that each resulting member of a pair is properly described by the same quantum mechanical description , which is...
replaces the word correlation, but the analogy is exact. A disentangled wavefunction has the form:
while an entangled wavefunction does not have this form. Like correlation in probability, there are many more entangled states than disentangled ones. For instance, when two particles which start out with an equal probability to be anywhere in a box have a strong attraction and a way to dissipate energy, they can easily come together to make a bound state. The bound state still has an equal probability to be anywhere, so that each particle is still equally likely to be anywhere, but the two particles are now entangled: so wherever one particle is, the other is too.
Analogy with probability
In probability theoryProbability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
there is a similar principle. If a system has a probabilistic description, this description gives the probability of any configuration, and given any two different configurations, there is a state which is partly this and partly that, with positive real number coefficients, the probabilities, which say how much of each there is.
For example, if we have a probability distribution for where a particle is, it is described by the "state"
Where
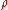is the probability densityProbability density
Probability density may refer to:* Probability density function in probability theory* The product of the probability amplitude with its complex conjugate in quantum mechanics...
function, a positive number that measures the probability that the particle will be found at a certain location.
The evolution equation is also linear in probability, for fundamental reasons. If the particle has some probability for going from position x to y, and from z to y, the probability of going to y starting from a state which is half-x and half-z is a half-and-half mixture of the probability of going to y from each of the options. This is the principle of linear superposition in probability.
Quantum mechanics is different, because the numbers can be positive or negative. While the complex nature of the numbers is just a doubling, if you consider the real and imaginary parts separately, the sign of the coefficients is important. In probability, two different possible outcomes always add together, so that if there are more options to get to a point z, the probability always goes up. In quantum mechanics, different possibilities can cancel.
In probability theory with a finite number of states, the probabilities can always be multiplied by a positive number to make their sum equal to one. For example, if there is a three state probability system:
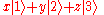
where the probabilities
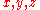are positive numbers. Rescaling x,y,z so thatThe geometry of the state space is a revealed to be a triangle. In general it is a simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
. There are special points in a triangle or simplex corresponding to the corners, and these points are those where one of the probabilities is equal to 1 and the others are zero. These are the unique locations where the position is known with certainty.
In a quantum mechanical system with three states, the quantum mechanical wavefunction is a superposition of states again, but this time twice as many quantities with no restriction on the sign:
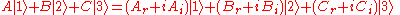
rescaling the variables so that the sum of the squares is 1, the geometry of the space is revealed to be a high dimensional sphere
.A sphere has a large amount of symmetry, it can be viewed in different coordinate systems or bases
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
. So unlike a probability theory, a quantum theory has a large number of different bases in which it can be equally well described. The geometry of the phase space can be viewed as a hint that the quantity in quantum mechanics which corresponds to the probability is the absolute square of the coefficient of the superposition.
Hamiltonian evolution
The numbers that describe the amplitudes for different possibilities define the kinematics, the space of different states. The dynamics describes how these numbers change with time. For a particle that can be in any one of infinitely many discrete positions, a particle on a lattice, the superposition principle tells you how to make a state: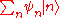So that the infinite list of amplitudes
completely describes the quantum state of the particle. This list is called the state vector, and formally it is an element of a Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
, an infinite dimensional complex vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
. It is usual to represent the state so that the sum of the absolute squares of the amplitudes add up to one:
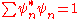
For a particle described by probability theory random walking on a line, the analogous thing is the list of probabilities
, which give the probability of any position. The quantities that describe how they change in time are the transition probabilities 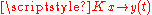, which gives the probability that, starting at x, the particle ends up at y after time t. The total probability of ending up at y is given by the sum over all the possibilities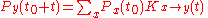The condition of conservation of probability states that starting at any x, the total probability to end up somewhere must add up to 1:
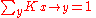
So that the total probability will be preserved, K is what is called a stochastic matrix
Stochastic matrix
In mathematics, a stochastic matrix is a matrix used to describe the transitions of a Markov chain. It has found use in probability theory, statistics and linear algebra, as well as computer science...
.
When no time passes, nothing changes: for zero elapsed time
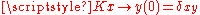, the K matrix is zero except from a state to itself. So in the case that the time is short, it is better to talk about the rate of change of the probability instead of the absolute change in the probability.where
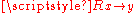is the time derivative of the K matrix: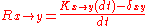.The equation for the probabilities is a differential equation which is sometimes called the master equation:
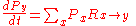
The R matrix is the probability per unit time for the particle to make a transition from x to y. The condition that the K matrix elements add up to one becomes the condition that the R matrix elements add up to zero:
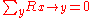
One simple case to study is when the R matrix has an equal probability to go one unit to the left or to the right, describing a particle which has a constant rate of random walking. In this case
is zero unless y is either x+1,x, or x−1, when y is x+1 or x−1, the R matrix has value c, and in order for the sum of the R matrix coefficients to equal zero, the value of must be −2c. So the probabilities obey the discretized diffusion equation: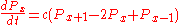which, when c is scaled appropriately and the P distribution is smooth enough to think of the system in a continuum limit becomes:
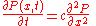
Which is the diffusion equation.
Quantum amplitudes give the rate at which amplitudes change in time, and they are mathematically exactly the same except that they are complex numbers. The analog of the finite time K matrix is called the U matrix:
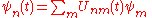
Since the sum of the absolute squares of the amplitudes must be constant,
must be unitary: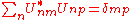or, in matrix notation,
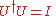
The rate of change of U is called the Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
H, up to a traditional factor of i:
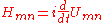
The Hamiltonian gives the rate at which the particle has an amplitude to go from m to n. The reason it is multiplied by i is that the condition that U is unitary translates to the condition:
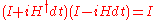
which says that H is Hermitian
Hermitian
A number of mathematical entities are named Hermitian, after the mathematician Charles Hermite:*Hermitian adjoint*Hermitian connection, the unique connection on a Hermitian manifold that satisfies specific conditions...
. The eigenvalues of the Hermitian matrix H are real quantities which have a physical interpretation as energy levels. If the factor i were absent, the H matrix would be antihermitian and would have purely imaginary eigenvalues, which is not the traditional way quantum mechanics represents observable quantities like the energy.
For a particle which has equal amplitude to move left and right, the Hermitian matrix H is zero except for nearest neighbors, where it has the value c. If the coefficient is everywhere constant, the condition that H is Hermitian demands that the amplitude to move to the left is the complex conjugate of the amplitude to move to the right. The equation of motion for
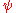is the time differential equation: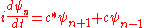In the case that left and right are symmetric, c is real. By redefining the phase of the wavefunction in time,
, the amplitudes for being at different locations are only rescaled, so that the physical situation is unchanged. But this phase rotation introduces a linear term.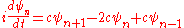which is the right choice of phase to take the continuum limit. When c is very large and psi is slowly varying so that the lattice can be thought of as a line, this becomes the free Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
:
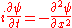
If there is an additional term in the H matrix which is an extra phase rotation which varies from point to point, the continuum limit is the Schrödinger equation with a potential energy:
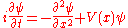
These equations describe the motion of a single particle in non-relativistic quantum mechanics.
Quantum mechanics in imaginary time
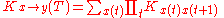
The analogy between quantum mechanics and probability is very strong, so that there are many mathematical links between them. In a statistical system in discrete time, t=1,2,3, described by a transition matrix for one time step, the probability to go between two points after a finite number of time steps can be represented as a sum over all paths of the probability of taking each path:where the sum extends over all paths
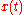with the property that 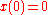and . The analogous expression in quantum mechanics is the path integralPath integral formulation
The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
.
A generic transition matrix in probability has a stationary distribution, which is the eventual probability to be found at any point no matter what the starting point. If there is a nonzero probability for any two paths to reach the same point at the same time, this stationary distribution does not depend on the initial conditions. In probability theory, the probability m for the stochastic matrix obeys detailed balance
Detailed balance
The principle of detailed balance is formulated for kinetic systems which are decomposed into elementary processes : At equilibrium, each elementary process should be equilibrated by its reverse process....
when the stationary distribution
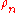has the property: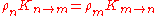Detailed balance says that the total probability of going from m to n in the stationary distribution, which is the probability of starting at m
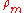times the probability of hopping from m to n, is equal to the probability of going from n to m, so that the total back-and-forth flow of probability in equilibrium is zero along any hop. The condition is automatically satisfied when n=m, so it has the same form when written as a condition for the transition-probability R matrix.When the R matrix obeys detailed balance, the scale of the probabilities can be redefined using the stationary distribution so that they no longer sum to 1:
In the new coordinates, the R matrix is rescaled as follows:
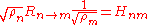
and H is symmetric
This matrix H defines a quantum mechanical system:
whose Hamiltonian has the same eigenvalues as those of the R matrix of the statistical system. The eigenvectors are the same too, except expressed in the rescaled basis. The stationary distribution of the statistical system is the ground state of the Hamiltonian and it has energy exactly zero, while all the other energies are positive. If H is exponentiated to find the U matrix:
and t is allowed to take on complex values, the K' matrix is found by taking time imaginary.
For quantum systems which are invariant under time reversal
Time reversal
Time reversal may refer to:* In physics, T-symmetry - the study of thermodynamics and the symmetry of certain physical laws where the concept of time is reversed — ie...
the Hamiltonian can be made real and symmetric, so that the action of time-reversal on the wave-function is just complex conjugation. If such a Hamiltonian has a unique lowest energy state with a positive real wave-function, as it often does for physical reasons, it is connected to a stochastic system in imaginary time. This relationship between stochastic systems and quantum systems sheds much light on supersymmetry
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
.
Experiments and applications
Successful experiments involving superpositions of relatively large (by the standards of quantum physics) objects have been performed.- A "cat state" has been achieved with photonPhotonIn physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
s. - A berylliumBerylliumBeryllium is the chemical element with the symbol Be and atomic number 4. It is a divalent element which occurs naturally only in combination with other elements in minerals. Notable gemstones which contain beryllium include beryl and chrysoberyl...
ionIonAn ion is an atom or molecule in which the total number of electrons is not equal to the total number of protons, giving it a net positive or negative electrical charge. The name was given by physicist Michael Faraday for the substances that allow a current to pass between electrodes in a...
has been trapped in a superposed state. - A double slit experiment has been performed with molecules as large as buckyballsBuckminsterfullereneBuckminsterfullerene is a spherical fullerene molecule with the formula . It was first intentionally prepared in 1985 by Harold Kroto, James Heath, Sean O'Brien, Robert Curl and Richard Smalley at Rice University...
. - An experiment involving a superconducting quantum interference device ("SQUID") has been linked to theme of the thought experiment: " The superposition state does not correspond to a billion electrons flowing one way and a billion others flowing the other way. Superconducting electrons move en masse. All the superconducting electrons in the SQUID flow both ways around the loop at once when they are in the Schrödinger’s cat state.".
- A piezoelectric "tuning forkTuning forkA tuning fork is an acoustic resonator in the form of a two-pronged fork with the prongs formed from a U-shaped bar of elastic metal . It resonates at a specific constant pitch when set vibrating by striking it against a surface or with an object, and emits a pure musical tone after waiting a...
" has been constructed, which can be placed into a superposition of vibrating and non vibrating states. The resonator comprises about 10 trillion atoms. - An experiment involving a flu virus has been proposed.
In quantum computing the phrase "cat state" often refers to the special entanglement of qubit
Qubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
s wherein the qubits are in an equal superposition of all being 0 and all being 1; i.e.,
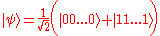.Formal interpretation
Applying the superposition principleSuperposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
to a quantum mechanical particle, the configurations of the particle are all positions, so the superpositions make a complex wave in space. The coefficients of the linear superposition are a wave which describes the particle as best as is possible, and whose amplitude interferes according to the Huygens principle.
For any physical property in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, there is a list of all the states where that property has some value. These states are necessarily perpendicular to each other using the Euclidean notion of perpendicularity which comes from sums-of-squares length, except that they also must not be i multiples of each other. This list of perpendicular states has an associated value which is the value of the physical property. The superposition principle guarantees that any state can be written as a combination of states of this form with complex coefficients.
Write each state with the value q of the physical quantity as a vector in some basis
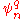, a list of numbers at each value of n for the vector which has value q for the physical quantity. Now form the outer product of the vectors by multiplying all the vector components and add them with coefficients to make the matrixwhere the sum extends over all possible values of q. This matrix is necessarily symmetric because it is formed from the orthogonal states, and has eigenvalues q. The matrix A is called the observable associated to the physical quantity. It has the property that the eigenvalues and eigenvectors determine the physical quantity and the states which have definite values for this quantity.
Every physical quantity has a Hermitian linear operator associated to it, and the states where the value of this physical quantity is definite are the eigenstates of this linear operator. The linear combination of two or more eigenstates results in quantum superposition of two or more values of the quantity. If the quantity is measured, the value of the physical quantity will be random, with a probability equal to the square of the coefficient of the superposition in the linear combination. Immediately after the measurement, the state will be given by the eigenvector corresponding to the measured eigenvalue.
It is natural to ask why "real" (macroscopic, Newtonian) objects and events do not seem to display quantum mechanical features such as superposition. In 1935, Erwin Schrödinger
Erwin Schrödinger
Erwin Rudolf Josef Alexander Schrödinger was an Austrian physicist and theoretical biologist who was one of the fathers of quantum mechanics, and is famed for a number of important contributions to physics, especially the Schrödinger equation, for which he received the Nobel Prize in Physics in 1933...
devised a well-known thought experiment, now known as Schrödinger's cat
Schrödinger's cat
Schrödinger's cat is a thought experiment, usually described as a paradox, devised by Austrian physicist Erwin Schrödinger in 1935. It illustrates what he saw as the problem of the Copenhagen interpretation of quantum mechanics applied to everyday objects. The scenario presents a cat that might be...
, which highlighted the dissonance between quantum mechanics and Newtonian physics, where only one configuration occurs, although a configuration for a particle in Newtonian physics specifies both position and momentum.
In fact, quantum superposition results in many directly observable effects, such as interference peaks from an electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
wave
Wave
In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
in a double-slit experiment
Double-slit experiment
The double-slit experiment, sometimes called Young's experiment, is a demonstration that matter and energy can display characteristics of both waves and particles...
. The superpositions, however, persist at all scales, absent a mechanism for removing them. This mechanism can be philosophical as in the Copenhagen interpretation
Copenhagen interpretation
The Copenhagen interpretation is one of the earliest and most commonly taught interpretations of quantum mechanics. It holds that quantum mechanics does not yield a description of an objective reality but deals only with probabilities of observing, or measuring, various aspects of energy quanta,...
, or physical.
Recent research indicates that chlorophyll
Chlorophyll
Chlorophyll is a green pigment found in almost all plants, algae, and cyanobacteria. Its name is derived from the Greek words χλωρος, chloros and φύλλον, phyllon . Chlorophyll is an extremely important biomolecule, critical in photosynthesis, which allows plants to obtain energy from light...
within plants appears to exploit the feature of quantum superposition to achieve greater efficiency in transporting energy, allowing pigment proteins to be spaced further apart than would otherwise be possible.
If the operators corresponding to two observables do not commute
Commute
Commute, commutation or commutative may refer to:* Commuting, the process of travelling between a place of residence and a place of work* Commutative property, a property of a mathematical operation...
, they have no simultaneous eigenstates and they obey an uncertainty principle
Uncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
. A state where one observable has a definite value corresponds to a superposition of many states for the other observable.
See also
- Wave packetWave packetIn physics, a wave packet is a short "burst" or "envelope" of wave action that travels as a unit. A wave packet can be analyzed into, or can be synthesized from, an infinite set of component sinusoidal waves of different wavenumbers, with phases and amplitudes such that they interfere...
- Quantum computation
- Penrose InterpretationPenrose interpretationThe Penrose interpretation is a prediction of Sir Roger Penrose about the relationship between quantum mechanics and general relativity. Penrose proposes that a quantum state remains in superposition until the difference of space-time curvature attains a significant level...
- Mach-Zehnder interferometerMach-Zehnder interferometerThe Mach–Zehnder interferometer is a device used to determine the relative phase shift between two collimated beams from a coherent light source. The interferometer has been used, amongst other things, to measure small phase shifts in one of the two beams caused by a small sample or the change in...
- Pure qubit state
- Schrödinger's catSchrödinger's catSchrödinger's cat is a thought experiment, usually described as a paradox, devised by Austrian physicist Erwin Schrödinger in 1935. It illustrates what he saw as the problem of the Copenhagen interpretation of quantum mechanics applied to everyday objects. The scenario presents a cat that might be...