Symplectic matrix
Encyclopedia
Let M be a 2n×2n matrix
with real
entries. Then M is called a symplectic matrix if it satisfies the condition
where MT denotes the transpose
of M and Ω is a fixed nonsingular, skew-symmetric matrix
. Typically Ω is chosen to be the block matrix
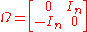
where In is the n×n identity matrix
. Note that Ω has determinant
+1 and has an inverse given by Ω−1 = ΩT = −Ω.
Furthermore, the product
of two symplectic matrices is, again, a symplectic matrix. This gives the set of all symplectic matrices the structure of a group
. There exists a natural manifold
structure on this group which makes it into a (real or complex) Lie group
called the symplectic group
. The symplectic group has dimension n(2n + 1).
It follows easily from the definition that the determinant
of any symplectic matrix is ±1. Actually, it turns out that the determinant is always +1. One way to see this is through the use of the Pfaffian
and the identity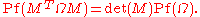
Since
and 
we have that det(M) = 1.
Suppose Ω is given in the standard form and let M be a 2n×2n block matrix
given by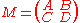
where A, B, C, D are n×n matrices. The condition for M to be symplectic is equivalent to the conditions
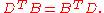
When n = 1 these conditions reduce to the single condition det(M) = 1. Thus a 2×2 matrix is symplectic iff
it has unit determinant.
, matrices are replaced with linear transformation
s of finite-dimensional vector spaces. The abstract analog of a symplectic matrix is a symplectic transformation of a symplectic vector space
. Briefly, a symplectic vector space is a 2n-dimensional vector space V equipped with a nondegenerate, skew-symmetric bilinear form ω called the symplectic form.
A symplectic transformation is then a linear transformation L : V → V which preserves ω, i.e.
Fixing a basis
for V, ω can be written as a matrix Ω and L as a matrix M. The condition that L be a symplectic transformation is precisely the condition that M be a symplectic matrix: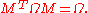
Under a change of basis
, represented by a matrix A, we have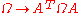
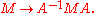
One can always bring Ω to either of the standard forms given in the introduction by a suitable choice of A.
Ω. As explained in the previous section, Ω can be thought of as the coordinate representation of a nondegenerate skew-symmetric bilinear form. It is a basic result in linear algebra
that any two such matrices differ from each other by a change of basis
.
The most common alternative to the standard Ω given above is the block diagonal form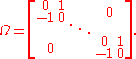
This choice differs from the previous one by a permutation
of basis vectors.
Sometimes the notation J is used instead of Ω for the skew-symmetric matrix. This is a particularly unfortunate choice as it leads to confusion with the notion of a complex structure
, which often has the same coordinate expression as Ω but represents a very different structure. A complex structure J is the coordinate representation of a linear transformation that squares to −1, whereas Ω is the coordinate representation of a nondegenerate skew-symmetric bilinear form. One could easily choose bases in which J is not skew-symmetric or Ω does not square to −1.
Given a hermitian structure on a vector space, J and Ω are related via
where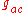
is the metric
. That J and Ω usually have the same coordinate expression (up to an overall sign) is simply a consequence of the fact that the metric g is usually the identity matrix.
with complex
entries, the definition is not standard throughout the literature. Many authors adjust the definition above to
where M* denotes the conjugate transpose
of M. Other authors retain the definition for complex matrices and call matrices satisfying conjugate symplectic.
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
with real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
entries. Then M is called a symplectic matrix if it satisfies the condition
where MT denotes the transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
of M and Ω is a fixed nonsingular, skew-symmetric matrix
Skew-symmetric matrix
In mathematics, and in particular linear algebra, a skew-symmetric matrix is a square matrix A whose transpose is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e...
. Typically Ω is chosen to be the block matrix
Block matrix
In the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...
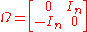
where In is the n×n identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
. Note that Ω has determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
+1 and has an inverse given by Ω−1 = ΩT = −Ω.
Properties
Every symplectic matrix is invertible with the inverse matrix given byFurthermore, the product
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
of two symplectic matrices is, again, a symplectic matrix. This gives the set of all symplectic matrices the structure of a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. There exists a natural manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
structure on this group which makes it into a (real or complex) Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
called the symplectic group
Symplectic group
In mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...
. The symplectic group has dimension n(2n + 1).
It follows easily from the definition that the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of any symplectic matrix is ±1. Actually, it turns out that the determinant is always +1. One way to see this is through the use of the Pfaffian
Pfaffian
In mathematics, the determinant of a skew-symmetric matrix can always be written as the square of a polynomial in the matrix entries. This polynomial is called the Pfaffian of the matrix, The term Pfaffian was introduced by who named them after Johann Friedrich Pfaff...
and the identity
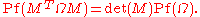
Since
and we have that det(M) = 1.Suppose Ω is given in the standard form and let M be a 2n×2n block matrix
Block matrix
In the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...
given by
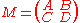
where A, B, C, D are n×n matrices. The condition for M to be symplectic is equivalent to the conditions
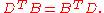
When n = 1 these conditions reduce to the single condition det(M) = 1. Thus a 2×2 matrix is symplectic iff
IFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
it has unit determinant.
Symplectic transformations
In the abstract formulation of linear algebraLinear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, matrices are replaced with linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
s of finite-dimensional vector spaces. The abstract analog of a symplectic matrix is a symplectic transformation of a symplectic vector space
Symplectic vector space
In mathematics, a symplectic vector space is a vector space V equipped with a bilinear form ω : V × V → R that is...
. Briefly, a symplectic vector space is a 2n-dimensional vector space V equipped with a nondegenerate, skew-symmetric bilinear form ω called the symplectic form.
A symplectic transformation is then a linear transformation L : V → V which preserves ω, i.e.
Fixing a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
for V, ω can be written as a matrix Ω and L as a matrix M. The condition that L be a symplectic transformation is precisely the condition that M be a symplectic matrix:
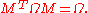
Under a change of basis
Change of basis
In linear algebra, change of basis refers to the conversion of vectors and linear transformations between matrix representations which have different bases.-Expression of a basis:...
, represented by a matrix A, we have
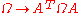
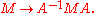
One can always bring Ω to either of the standard forms given in the introduction by a suitable choice of A.
The matrix Ω
Symplectic matrices are defined relative to a fixed nonsingular, skew-symmetric matrixSkew-symmetric matrix
In mathematics, and in particular linear algebra, a skew-symmetric matrix is a square matrix A whose transpose is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e...
Ω. As explained in the previous section, Ω can be thought of as the coordinate representation of a nondegenerate skew-symmetric bilinear form. It is a basic result in linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
that any two such matrices differ from each other by a change of basis
Change of basis
In linear algebra, change of basis refers to the conversion of vectors and linear transformations between matrix representations which have different bases.-Expression of a basis:...
.
The most common alternative to the standard Ω given above is the block diagonal form
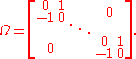
This choice differs from the previous one by a permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
of basis vectors.
Sometimes the notation J is used instead of Ω for the skew-symmetric matrix. This is a particularly unfortunate choice as it leads to confusion with the notion of a complex structure
Linear complex structure
In mathematics, a complex structure on a real vector space V is an automorphism of V that squares to the minus identity, −I. Such a structure on V allows one to define multiplication by complex scalars in a canonical fashion so as to regard V as a complex vector space.Complex structures have...
, which often has the same coordinate expression as Ω but represents a very different structure. A complex structure J is the coordinate representation of a linear transformation that squares to −1, whereas Ω is the coordinate representation of a nondegenerate skew-symmetric bilinear form. One could easily choose bases in which J is not skew-symmetric or Ω does not square to −1.
Given a hermitian structure on a vector space, J and Ω are related via
where
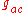is the metricMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
. That J and Ω usually have the same coordinate expression (up to an overall sign) is simply a consequence of the fact that the metric g is usually the identity matrix.
Complex matrices
If instead M is a 2n×2n matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
with complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
entries, the definition is not standard throughout the literature. Many authors adjust the definition above to
where M* denotes the conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
of M. Other authors retain the definition for complex matrices and call matrices satisfying conjugate symplectic.
See also
- symplectic vector spaceSymplectic vector spaceIn mathematics, a symplectic vector space is a vector space V equipped with a bilinear form ω : V × V → R that is...
- symplectic groupSymplectic groupIn mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...
- symplectic representationSymplectic representationIn mathematical field of representation theory, a quaternionic representation is a representation on a complex vector space V with an invariant quaternionic structure, i.e., an antilinear equivariant mapj\colon V\to V\,which satisfiesj^2=-1.\,...
- orthogonal matrixOrthogonal matrixIn linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
- unitary matrix
- Hamiltonian mechanicsHamiltonian mechanicsHamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...