
Skew-symmetric matrix
Encyclopedia
In mathematics, and in particular linear algebra
, a skew-symmetric (or antisymmetric or antimetric) matrix is a square matrix A whose transpose
is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e. then the symmetric condition becomes For example, the following matrix is skew-symmetric:

is not of characteristic
2: that is, that where 1 denotes the multiplicative identity and 0 the additive identity of the given field. Otherwise, a skew-symmetric matrix is just the same thing as a symmetric matrix.
Sums and scalar multiples of skew-symmetric matrices are again skew-symmetric. Hence, the skew-symmetric matrices form a vector space
. Its dimension is n(n−1)/2.
Let Matn denote the space of matrices. A skew-symmetric matrix is determined by n(n − 1)/2 scalars (the number of entries above the main diagonal); a symmetric matrix is determined by n(n + 1)/2 scalars (the number of entries on or above the main diagonal). If Skewn denotes the space of skew-symmetric matrices and Symn denotes the space of symmetric matrices and then since and }, i.e.
where ⊕ denotes the direct sum
. Let then
Notice that and This is true for every square matrix A with entries from any field
whose characteristic
is different from 2.
As to equivalent conditions, notice that the relation of skew-symmetricity, A=-AT, holds for a matrix A if and only if one has xTAy =-yTAx for all vectors x and y. This is also equivalent to xTAx=0 for all x (one implication being obvious, the other a plain consequence of (x+y)TA(x+y)=0 for all x and y).
All main diagonal entries of a skew-symmetric matrix must be zero, so the trace is zero. If is skew-symmetric, ; hence
3x3 skew symmetric matrices can be used to represent cross product
s as matrix multiplications.
of A satisfies
In particular, if n is odd, and since the underlying field is not of characteristic 2, the determinant vanishes. This result is called Jacobi's theorem, after Carl Gustav Jacobi (Eves, 1980).
The even-dimensional case is more interesting. It turns out that the determinant of A for n even can be written as the square of a polynomial
in the entries of A (Theorem by Thomas Muir
):
This polynomial is called the Pfaffian
of A and is denoted Pf(A). Thus the determinant of a real skew-symmetric matrix is always non-negative.
The number of distinct terms s(n) in the expansion of the determinant of a skew-symmetric matrix of order n has been considered already by Cayley, Sylvester, and Pfaff. Due to cancellations, this number is quite small as compared the number of terms of a generic matrix of order n, which is n!. The sequence s(n) is
and it is encoded in the exponential generating function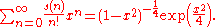
The latter yields to the asymptotics (for n even)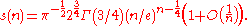
The number of positive and negative terms are approximatively a half of the total, although their difference takes larger and larger positive and negative values as n increases .
and thus are of the form iλ1, −iλ1, iλ2, −iλ2, … where each of the λk are real.
Real skew-symmetric matrices are normal matrices
(they commute with their adjoints) and are thus subject to the spectral theorem
, which states that any real skew-symmetric matrix can be diagonalized by a unitary matrix. Since the eigenvalues of a real skew-symmetric matrix are complex it is not possible to diagonalize one by a real matrix. However, it is possible to bring every skew-symmetric matrix to a block diagonal
form by an orthogonal transformation
. Specifically, every 2n × 2n real skew-symmetric matrix can be written in the form A = Q Σ QT where Q is orthogonal and
for real λk. The nonzero eigenvalues of this matrix are ±iλk. In the odd-dimensional case Σ always has at least one row and column of zeros.
More generally, every complex skew-symmetric matrix can be written in the form A = U Σ UT where U is unitary and Σ has the block-diagonal form given above with complex λk. This is an example of the Youla decomposition of a complex square matrix.
V over a field
K, not of characteristic
2, is defined to be a bilinear form
such that
This defines a form with desirable properties for vector spaces over fields of characteristic not equal to 2, but in a vector space over a field of characteristic 2, the definition fails, as every element is its own additive inverse. That is, symmetric and alternating forms are equivalent, which is clearly false in the case above. However, we may extend the definition to vector spaces over fields of characteristic 2 as follows:
In the case where the vector space
V is over a field of arbitrary characteristic
including characteristic 2, we may state that for all vectors v in V
This reduces to the above case when the field is not of characteristic 2 as seen below
Whence,
Thus, we have a definition that now holds for vector spaces over fields of all characteristics.
Such a φ will be represented by a skew-symmetric matrix A, φ(v, w) = vTAw, once a basis
of V is chosen; and conversely an n×n skew-symmetric matrix A on Kn gives rise to an alternating form sending x to xTAx.
to the real orthogonal group
O(n) at the identity matrix; formally, the special orthogonal Lie algebra. In this sense, then, skew-symmetric matrices can be thought of as infinitesimal rotations.
Another way of saying this is that the space of skew-symmetric matrices forms the Lie algebra
o(n) of the Lie group
O(n).
The Lie bracket on this space is given by the commutator
:
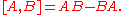
It is easy to check that the commutator of two skew-symmetric matrices is again skew-symmetric:

The matrix exponential
of a skew-symmetric matrix A is then an orthogonal matrix
R:
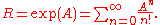
The image of the exponential map
of a Lie algebra always lies in the connected component
of the Lie group that contains the identity element. In the case of the Lie group O(n), this connected component is the special orthogonal group SO(n), consisting of all orthogonal matrices with determinant 1. So R = exp(A) will have determinant +1. Moreover, since the exponential map of a connected compact Lie group is always surjective, it turns out that every orthogonal matrix with unit determinant can be written as the exponential of some skew-symmetric matrix. In the particular important case of dimension n=2, the exponential representation for an orthogonal matrix reduces to the well-known polar form of a complex number of unit modulus. Indeed, if n=2, a special orthogonal matrix has the form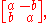
with a2+b2=1. Therefore, putting a=cosθ and b=sinθ, it can be written
which corresponds exactly to the polar form cosθ + isinθ =eiθ of a complex number of unit modulus. The exponential representation of an orthogonal matrix of order n can also be obtained starting from the fact that in dimension n any special orthogonal matrix R can be written as R = Q S QT, where Q is orthogonal and S is a block diagonal matrix with blocks of order 2, plus one of order 1 if n is odd; since each single block of order 2 is also an orthogonal matrix, it admits an exponential form. Correspondingly, the matrix S writes as exponential of a skew-symmetric block matrix Σ of the form above, S=exp(Σ), so that R= Q exp(Σ)QT =exp(Q Σ QT), exponential of the skew-symmetric matrix Q Σ QT. Conversely, the surjectivity of the exponential map, together with the above mentioned block-diagonalization for skew-simmetric matrices, implies the block-diagonalization for orthogonal matrices.
blocks of order 2, plus one of order 1 if n is odd; since each single block of order 2 is also an orthogonal matrix, it admits an exponential form. Correspondingly, the matrix S writes as exponential of a skew-symmetric block matrix Σ of the form above, S=exp(Σ), so that R= Q exp(Σ)QT =exp(Q Σ QT), exponential of the skew-symmetric matrix Q Σ QT. Conversely, the surjectivity of the exponential map, together with the above mentioned block-diagonalization for skew-simmetric matrices, implies the block-diagonalization for orthogonal matrices.
s on the space, which are sums of simple bivectors (2-blades) . The correspondence is given by the map
. The correspondence is given by the map  where
where  is the covector dual to the vector v; in orthonormal coordinates these are exactly the elementary skew-symmetric matrices. This characterization is used in interpreting the curl of a vector field (naturally a 2-vector) as an infinitesimal rotation or "curl", hence the name.
is the covector dual to the vector v; in orthonormal coordinates these are exactly the elementary skew-symmetric matrices. This characterization is used in interpreting the curl of a vector field (naturally a 2-vector) as an infinitesimal rotation or "curl", hence the name.
D and skew-symmetric matrix S such that For real n-by-n matrices, sometimes the condition for D to have positive entries is added.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a skew-symmetric (or antisymmetric or antimetric) matrix is a square matrix A whose transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e. then the symmetric condition becomes For example, the following matrix is skew-symmetric:

Properties
We assume that the underlying fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
is not of characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
2: that is, that where 1 denotes the multiplicative identity and 0 the additive identity of the given field. Otherwise, a skew-symmetric matrix is just the same thing as a symmetric matrix.
Sums and scalar multiples of skew-symmetric matrices are again skew-symmetric. Hence, the skew-symmetric matrices form a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
. Its dimension is n(n−1)/2.
Let Matn denote the space of matrices. A skew-symmetric matrix is determined by n(n − 1)/2 scalars (the number of entries above the main diagonal); a symmetric matrix is determined by n(n + 1)/2 scalars (the number of entries on or above the main diagonal). If Skewn denotes the space of skew-symmetric matrices and Symn denotes the space of symmetric matrices and then since and }, i.e.

where ⊕ denotes the direct sum
Direct sum of modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
. Let then

Notice that and This is true for every square matrix A with entries from any field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
whose characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
is different from 2.
As to equivalent conditions, notice that the relation of skew-symmetricity, A=-AT, holds for a matrix A if and only if one has xTAy =-yTAx for all vectors x and y. This is also equivalent to xTAx=0 for all x (one implication being obvious, the other a plain consequence of (x+y)TA(x+y)=0 for all x and y).
All main diagonal entries of a skew-symmetric matrix must be zero, so the trace is zero. If is skew-symmetric, ; hence
3x3 skew symmetric matrices can be used to represent cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
s as matrix multiplications.
Determinant
Let A be a n×n skew-symmetric matrix. The determinantDeterminant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of A satisfies
- det(A) = det(AT) = det(−A) = (−1)ndet(A). Hence when n is odd.
In particular, if n is odd, and since the underlying field is not of characteristic 2, the determinant vanishes. This result is called Jacobi's theorem, after Carl Gustav Jacobi (Eves, 1980).
The even-dimensional case is more interesting. It turns out that the determinant of A for n even can be written as the square of a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
in the entries of A (Theorem by Thomas Muir
Thomas Muir (mathematician)
Sir Thomas Muir FRS was a Scottish mathematician, remembered as an authority on determinants. He was born in Stonebyres in South Lanarkshire, and brought up in the small town of Biggar. At the University of Glasgow he changed his studies from classics to mathematics after advice from the future...
):
- det(A) = Pf(A)2.
This polynomial is called the Pfaffian
Pfaffian
In mathematics, the determinant of a skew-symmetric matrix can always be written as the square of a polynomial in the matrix entries. This polynomial is called the Pfaffian of the matrix, The term Pfaffian was introduced by who named them after Johann Friedrich Pfaff...
of A and is denoted Pf(A). Thus the determinant of a real skew-symmetric matrix is always non-negative.
The number of distinct terms s(n) in the expansion of the determinant of a skew-symmetric matrix of order n has been considered already by Cayley, Sylvester, and Pfaff. Due to cancellations, this number is quite small as compared the number of terms of a generic matrix of order n, which is n!. The sequence s(n) is
- 1, 0, 2, 0, 6, 0, 120, 0, 5250, 0, 395010, 0, …
and it is encoded in the exponential generating function
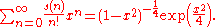
The latter yields to the asymptotics (for n even)
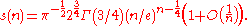
The number of positive and negative terms are approximatively a half of the total, although their difference takes larger and larger positive and negative values as n increases .
Spectral theory
The eigenvalues of a skew-symmetric matrix always come in pairs ±λ (except in the odd-dimensional case where there is an additional unpaired 0 eigenvalue). For a real skew-symmetric matrix the nonzero eigenvalues are all pure imaginaryImaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
and thus are of the form iλ1, −iλ1, iλ2, −iλ2, … where each of the λk are real.
Real skew-symmetric matrices are normal matrices
Normal matrix
A complex square matrix A is a normal matrix ifA^*A=AA^* \ where A* is the conjugate transpose of A. That is, a matrix is normal if it commutes with its conjugate transpose.If A is a real matrix, then A*=AT...
(they commute with their adjoints) and are thus subject to the spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
, which states that any real skew-symmetric matrix can be diagonalized by a unitary matrix. Since the eigenvalues of a real skew-symmetric matrix are complex it is not possible to diagonalize one by a real matrix. However, it is possible to bring every skew-symmetric matrix to a block diagonal
Block matrix
In the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...
form by an orthogonal transformation
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
. Specifically, every 2n × 2n real skew-symmetric matrix can be written in the form A = Q Σ QT where Q is orthogonal and

for real λk. The nonzero eigenvalues of this matrix are ±iλk. In the odd-dimensional case Σ always has at least one row and column of zeros.
More generally, every complex skew-symmetric matrix can be written in the form A = U Σ UT where U is unitary and Σ has the block-diagonal form given above with complex λk. This is an example of the Youla decomposition of a complex square matrix.
Alternating forms
We begin with a special case of the definition. An alternating form φ on a vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K, not of characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
2, is defined to be a bilinear form
- φ : V × V → K
such that
- φ(v,w) = −φ(w,v).
This defines a form with desirable properties for vector spaces over fields of characteristic not equal to 2, but in a vector space over a field of characteristic 2, the definition fails, as every element is its own additive inverse. That is, symmetric and alternating forms are equivalent, which is clearly false in the case above. However, we may extend the definition to vector spaces over fields of characteristic 2 as follows:
In the case where the vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V is over a field of arbitrary characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
including characteristic 2, we may state that for all vectors v in V
- φ(v,v) = 0.
This reduces to the above case when the field is not of characteristic 2 as seen below
- 0 = φ(v + w,v + w) = φ(v,v) + φ(v,w) + φ(w,v) + φ(w,w) = φ(v,w) + φ(w,v)
Whence,
- φ(v,w) = −φ(w,v).
Thus, we have a definition that now holds for vector spaces over fields of all characteristics.
Such a φ will be represented by a skew-symmetric matrix A, φ(v, w) = vTAw, once a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
of V is chosen; and conversely an n×n skew-symmetric matrix A on Kn gives rise to an alternating form sending x to xTAx.
Infinitesimal rotations
Skew-symmetric matrices over the field of real numbers form the tangent spaceTangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
to the real orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
O(n) at the identity matrix; formally, the special orthogonal Lie algebra. In this sense, then, skew-symmetric matrices can be thought of as infinitesimal rotations.
Another way of saying this is that the space of skew-symmetric matrices forms the Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
o(n) of the Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
O(n).
The Lie bracket on this space is given by the commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
:
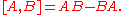
It is easy to check that the commutator of two skew-symmetric matrices is again skew-symmetric:

The matrix exponential
Matrix exponential
In mathematics, the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. Abstractly, the matrix exponential gives the connection between a matrix Lie algebra and the corresponding Lie group....
of a skew-symmetric matrix A is then an orthogonal matrix
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
R:
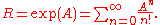
The image of the exponential map
Exponential map
In differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....
of a Lie algebra always lies in the connected component
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
of the Lie group that contains the identity element. In the case of the Lie group O(n), this connected component is the special orthogonal group SO(n), consisting of all orthogonal matrices with determinant 1. So R = exp(A) will have determinant +1. Moreover, since the exponential map of a connected compact Lie group is always surjective, it turns out that every orthogonal matrix with unit determinant can be written as the exponential of some skew-symmetric matrix. In the particular important case of dimension n=2, the exponential representation for an orthogonal matrix reduces to the well-known polar form of a complex number of unit modulus. Indeed, if n=2, a special orthogonal matrix has the form
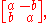
with a2+b2=1. Therefore, putting a=cosθ and b=sinθ, it can be written

which corresponds exactly to the polar form cosθ + isinθ =eiθ of a complex number of unit modulus. The exponential representation of an orthogonal matrix of order n can also be obtained starting from the fact that in dimension n any special orthogonal matrix R can be written as R = Q S QT, where Q is orthogonal and S is a block diagonal matrix with
 blocks of order 2, plus one of order 1 if n is odd; since each single block of order 2 is also an orthogonal matrix, it admits an exponential form. Correspondingly, the matrix S writes as exponential of a skew-symmetric block matrix Σ of the form above, S=exp(Σ), so that R= Q exp(Σ)QT =exp(Q Σ QT), exponential of the skew-symmetric matrix Q Σ QT. Conversely, the surjectivity of the exponential map, together with the above mentioned block-diagonalization for skew-simmetric matrices, implies the block-diagonalization for orthogonal matrices.
blocks of order 2, plus one of order 1 if n is odd; since each single block of order 2 is also an orthogonal matrix, it admits an exponential form. Correspondingly, the matrix S writes as exponential of a skew-symmetric block matrix Σ of the form above, S=exp(Σ), so that R= Q exp(Σ)QT =exp(Q Σ QT), exponential of the skew-symmetric matrix Q Σ QT. Conversely, the surjectivity of the exponential map, together with the above mentioned block-diagonalization for skew-simmetric matrices, implies the block-diagonalization for orthogonal matrices.Coordinate-free
More intrinsically (i.e., without using coordinates), skew-symmetric linear transformations on a vector space V with an inner product may be defined as the bivectorBivector
In mathematics, a bivector or 2-vector is a quantity in geometric algebra or exterior algebra that generalises the idea of a vector. If a scalar is considered a zero dimensional quantity, and a vector is a one dimensional quantity, then a bivector can be thought of as two dimensional. Bivectors...
s on the space, which are sums of simple bivectors (2-blades)
 . The correspondence is given by the map
. The correspondence is given by the map  where
where  is the covector dual to the vector v; in orthonormal coordinates these are exactly the elementary skew-symmetric matrices. This characterization is used in interpreting the curl of a vector field (naturally a 2-vector) as an infinitesimal rotation or "curl", hence the name.
is the covector dual to the vector v; in orthonormal coordinates these are exactly the elementary skew-symmetric matrices. This characterization is used in interpreting the curl of a vector field (naturally a 2-vector) as an infinitesimal rotation or "curl", hence the name.Skew-symmetrizable matrix
An n-by-n matrix A is said to be skew-symmetrizable if there exist an invertible diagonal matrixDiagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
D and skew-symmetric matrix S such that For real n-by-n matrices, sometimes the condition for D to have positive entries is added.
See also
- Symmetric matrix
- Skew-Hermitian matrixSkew-Hermitian matrixIn linear algebra, a square matrix with complex entries is said to be skew-Hermitian or antihermitian if its conjugate transpose is equal to its negative. That is, the matrix A is skew-Hermitian if it satisfies the relationA^\dagger = -A,\;...
- Symplectic matrix
- Symmetry in mathematicsSymmetry in mathematicsSymmetry occurs not only in geometry, but also in other branches of mathematics. It is actually the same as invariance: the property that something does not change under a set of transformations....

