Simple group
Encyclopedia
In mathematics
, a simple group is a nontrivial
group
whose only normal subgroup
s are the trivial group
and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group
, and the process can be repeated. If the group is finite
, then eventually one arrives at uniquely determined simple groups by the Jordan–Hölder theorem.
G = Z/3Z of congruence classes modulo
3 (see modular arithmetic
) is simple. If H is a subgroup of this group, its order (the number of elements) must be a divisor
of the order
of G which is 3. Since 3 is prime, its only divisors are 1 and 3, so either H is G, or H is the trivial group. On the other hand, the group G = Z/12Z is not simple. The set H of congruence classes of 0, 4, and 8 modulo 12 is a subgroup of order 3, and it is a normal subgroup since any subgroup of an abelian group
is normal. Similarly, the additive group Z of integer
s is not simple; the set of even integers is a non-trivial proper normal subgroup.
One may use the same kind of reasoning for any abelian group, to deduce that the only simple abelian groups are the cyclic group
s of prime
order
. The classification of nonabelian simple groups is far less trivial. The smallest nonabelian simple group is the alternating group A5 of order 60, and every simple group of order 60 is isomorphic
to A5. The second smallest nonabelian simple group is the projective special linear group PSL(2,7)
of order 168, and it is possible to prove that every simple group of order 168 is isomorphic to PSL(2,7)
.
s and the infinite Thompson groups
T and V are examples of these.
s are the basic building blocks of the integer
s. This is expressed by the Jordan–Hölder theorem which states that any two composition series
of a given group have the same length and the same factors, up to
permutation
and isomorphism
. In a huge collaborative effort, the classification of finite simple groups
was declared accomplished in 1983 by Daniel Gorenstein
, though some problems surfaced (specifically in the classification of quasithin group
s, which were plugged in 2004).
Briefly, finite simple groups are classified as lying in one of 18 families, or being one of 26 exceptions:
of Feit
and Thompson
states that every group of odd order is solvable
. Therefore every finite simple group has even order unless it is cyclic of prime order.
The Schreier conjecture
asserts that the group of outer automorphisms of every finite simple group is solvable
. This can be proved using the classification theorem.
, where Évariste Galois
realized that the fact that the alternating groups on five or more points was simple (and hence not solvable), which he proved in 1831, was the reason that one could not solve the quintic in radicals. Galois also constructed the projective special linear group of a plane over a prime finite field, PSL(2,p), and remarked that they were simple for p not 2 or 3. This is contained in his last letter to Chevalier, and are the next example of finite simple groups.
The next discoveries were by Camille Jordan
in 1870. Jordan had found 4 families of simple matrix groups over finite field
s of prime order, which are now known as the classical group
s.
At about the same time, it was shown that a family of five groups, called the Mathieu group
s and first described by Émile Léonard Mathieu
in 1861 and 1873, were also simple. Since these five groups were constructed by methods which did not yield infinitely many possibilities, they were called "sporadic
" by William Burnside
in his 1897 textbook.
Later Jordan's results on classical groups were generalized to arbitrary finite fields by Leonard Dickson, following the classification of complex simple Lie algebras by Wilhelm Killing
. Dickson also constructed exception groups of type G2 and E6 as well, but not of types F4, E7, or E8 . In the 1950s the work on groups of Lie type was continued, with Claude Chevalley
giving a uniform construction of the classical groups and the groups of exceptional type in a 1955 paper. This omitted certain known groups (the projective unitary groups), which were obtained by "twisting" the Chevalley construction. The remaining groups of Lie type were produced by Steinberg, Tits, and Herzig (who produced 3D4(q) and 2E6(q)) and by Suzuki and Ree (the Suzuki–Ree groups).
These groups (the groups of Lie type, together with the cyclic groups, alternating groups, and the five exceptional Mathieu groups) were believed to be a complete list, but after a lull of almost a century since the work of Mathieu, in 1964 the first Janko group
was discovered, and the remaining 20 sporadic groups were discovered or conjectured in 1965–1975, culminating in 1981, when Robert Griess announced that he had constructed Bernd Fischer
's "Monster group
". The Monster is the largest sporadic simple group having order of 808,017,424,794,512,875,886,459,904,961,710,757,005,754,368,000,000,000. The Monster has a faithful 196,883-dimensional representation in the 196,884-dimensional Griess algebra
, meaning that each element of the Monster can be expressed as a 196,883 by 196,883 matrix.
of 1962/63, largely lasting until 1983, but only being finished in 2004.
Soon after the construction of the Monster in 1981, a proof, totaling more than 10,000 pages, was supplied that group theorists had successfully listed all finite simple groups, with victory declared in 1983 by Daniel Gorenstein. This was premature – some gaps were later discovered, notably in the classification of quasithin group
s, which were eventually replaced in 2004 by a 1,300 page classification of quasithin groups, which is now generally accepted as complete.
Proof: If n is a prime-power, then a group of order n has a nontrivial center
and, therefore, is not simple. If n is not a prime power, then every Sylow subgroup is proper, and, by Sylow's Third Theorem, we know that the number of Sylow p-subgroups of a group of order n is equal to 1 modulo p and divides n. Since 1 is the only such number, the Sylow p-subgroup is unique, and therefore it is normal. Since it is a proper, non-identity subgroup, the group is not simple.
Burnside: A non-Abelian finite simple group has order divisible by at least three distinct primes. This follows from Burnside's p-q theorem
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a simple group is a nontrivial
Trivial group
In mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
whose only normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
s are the trivial group
Trivial group
In mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
, and the process can be repeated. If the group is finite
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
, then eventually one arrives at uniquely determined simple groups by the Jordan–Hölder theorem.
Examples
For example, the cyclic groupCyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
G = Z/3Z of congruence classes modulo
Modulo operation
In computing, the modulo operation finds the remainder of division of one number by another.Given two positive numbers, and , a modulo n can be thought of as the remainder, on division of a by n...
3 (see modular arithmetic
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
) is simple. If H is a subgroup of this group, its order (the number of elements) must be a divisor
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
of the order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
of G which is 3. Since 3 is prime, its only divisors are 1 and 3, so either H is G, or H is the trivial group. On the other hand, the group G = Z/12Z is not simple. The set H of congruence classes of 0, 4, and 8 modulo 12 is a subgroup of order 3, and it is a normal subgroup since any subgroup of an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
is normal. Similarly, the additive group Z of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s is not simple; the set of even integers is a non-trivial proper normal subgroup.
One may use the same kind of reasoning for any abelian group, to deduce that the only simple abelian groups are the cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
s of prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
. The classification of nonabelian simple groups is far less trivial. The smallest nonabelian simple group is the alternating group A5 of order 60, and every simple group of order 60 is isomorphic
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
to A5. The second smallest nonabelian simple group is the projective special linear group PSL(2,7)
PSL(2,7)
In mathematics, the projective special linear group PSL is a finite simple group that has important applications in algebra, geometry, and number theory. It is the automorphism group of the Klein quartic as well as the symmetry group of the Fano plane...
of order 168, and it is possible to prove that every simple group of order 168 is isomorphic to PSL(2,7)
PSL(2,7)
In mathematics, the projective special linear group PSL is a finite simple group that has important applications in algebra, geometry, and number theory. It is the automorphism group of the Klein quartic as well as the symmetry group of the Fano plane...
.
Infinite simple groups
Simple groups of infinite order also exist: simple Lie groupSimple Lie group
In group theory, a simple Lie group is a connected non-abelian Lie group G which does not have nontrivial connected normal subgroups.A simple Lie algebra is a non-abelian Lie algebra whose only ideals are 0 and itself...
s and the infinite Thompson groups
Thompson groups
In mathematics, the Thompson groups are three groups, commonly denoted F, T and V, which were first studied by the logician Richard Thompson in 1965...
T and V are examples of these.
Finite simple groups
The finite simple groups are important because in a certain sense they are the "basic building blocks" of all finite groups, somewhat similar to the way prime numberPrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s are the basic building blocks of the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s. This is expressed by the Jordan–Hölder theorem which states that any two composition series
Composition series
In abstract algebra, a composition series provides a way to break up an algebraic structure, such as a group or a module, into simple pieces. The need for considering composition series in the context of modules arises from the fact that many naturally occurring modules are not semisimple, hence...
of a given group have the same length and the same factors, up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
and isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
. In a huge collaborative effort, the classification of finite simple groups
Classification of finite simple groups
In mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
was declared accomplished in 1983 by Daniel Gorenstein
Daniel Gorenstein
Daniel E. Gorenstein was an American mathematician. He earned his undergraduate and graduate degrees at Harvard University, where he earned his Ph.D. in 1950 under Oscar Zariski, introducing in his dissertation Gorenstein rings...
, though some problems surfaced (specifically in the classification of quasithin group
Quasithin group
In mathematics, a quasithin group is roughly a finite simple group of characteristic 2 type and width 2. Here characteristic 2 type means that its centralizers of involutions resemble those of groups of Lie type over fields of characteristic 2, and the width is roughly the maximal rank of an...
s, which were plugged in 2004).
Briefly, finite simple groups are classified as lying in one of 18 families, or being one of 26 exceptions:
-
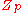– cyclic groupCyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of prime order -
– alternating group for 
- The alternating groups may be considered as groups of Lie type over the field with one elementField with one elementIn mathematics, the field with one element is a suggestive name for an object that should behave similarly to a finite field with a single element, if such a field could exist. This object is denoted F1, or, in a French-English pun, Fun...
, which unites this family with the next, and thus all families of non-abelian finite simple groups may be considered to be of Lie type.
- The alternating groups may be considered as groups of Lie type over the field with one element
- One of 16 families of groups of Lie type
- The Tits groupTits groupIn mathematics, the Tits group 2F4′ is a finite simple group of order 17971200 = 211 · 33 · 52 · 13 found by ....
is generally considered of this form, though strictly speaking it is not of Lie type, but rather index 2 in a group of Lie type.
- The Tits group
- One of 26 exceptions, the sporadic groupSporadic groupIn the mathematical field of group theory, a sporadic group is one of the 26 exceptional groups in the classification of finite simple groups. A simple group is a group G that does not have any normal subgroups except for the subgroup consisting only of the identity element, and G itself...
s, of which 20 are subgroups or subquotientSubquotientIn the mathematical fields of category theory and abstract algebra, a subquotient is a quotient object of a subobject. Subquotients are particularly important in group theory, where they are also known as sections, and in abelian categories....
s of the monster groupMonster groupIn the mathematical field of group theory, the Monster group M or F1 is a group of finite order:...
and are referred to as the "Happy Family", while the remaining 6 are referred to as pariahsPariah groupIn mathematical group theory, the term pariah was introduced by to refer to the six sporadic simple groups that are not subquotients of the monster simple group.These groups are:*Three of the Janko groups: J1, J3, and J4.*The Lyons group...
.
Structure
The famous theoremFeit–Thompson theorem
In mathematics, the Feit–Thompson theorem, or odd order theorem, states that every finite group of odd order is solvable. It was proved by - History : conjectured that every nonabelian finite simple group has even order...
of Feit
Walter Feit
Walter Feit was a Jewish Austrian-American mathematician who worked in finite group theory and representation theory....
and Thompson
John G. Thompson
John Griggs Thompson is a mathematician at the University of Florida noted for his work in the field of finite groups. He was awarded the Fields Medal in 1970, the Wolf Prize in 1992 and the 2008 Abel Prize....
states that every group of odd order is solvable
Solvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
. Therefore every finite simple group has even order unless it is cyclic of prime order.
The Schreier conjecture
Schreier conjecture
In finite group theory, the Schreier conjecture asserts that the group of outer automorphisms of every finite simple group is solvable. It was proposed by Otto Schreier in 1926, and is now known to be true as a result of the classification of finite simple groups, but no simpler proof is known....
asserts that the group of outer automorphisms of every finite simple group is solvable
Solvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
. This can be proved using the classification theorem.
History
There are two threads in the history of simple groups – the discovery and construction of specific simple groups and families, which took place from the work of Galois in the 1820s to the construction of the Monster in 1981; and proof that this list was complete, which began in the 19th century, most significantly took place 1955 through 1983 (when victory was initially declared), but was only generally agreed to be finished in 2004. , work on improving the proofs and understanding continues; see for 19th century history of simple groups.Construction
Simple groups have been studied at least since early Galois theoryGalois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
, where Évariste Galois
Évariste Galois
Évariste Galois was a French mathematician born in Bourg-la-Reine. While still in his teens, he was able to determine a necessary and sufficient condition for a polynomial to be solvable by radicals, thereby solving a long-standing problem...
realized that the fact that the alternating groups on five or more points was simple (and hence not solvable), which he proved in 1831, was the reason that one could not solve the quintic in radicals. Galois also constructed the projective special linear group of a plane over a prime finite field, PSL(2,p), and remarked that they were simple for p not 2 or 3. This is contained in his last letter to Chevalier, and are the next example of finite simple groups.
The next discoveries were by Camille Jordan
Camille Jordan
Marie Ennemond Camille Jordan was a French mathematician, known both for his foundational work in group theory and for his influential Cours d'analyse. He was born in Lyon and educated at the École polytechnique...
in 1870. Jordan had found 4 families of simple matrix groups over finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s of prime order, which are now known as the classical group
Classical group
In mathematics, the classical Lie groups are four infinite families of Lie groups closely related to the symmetries of Euclidean spaces. Their finite analogues are the classical groups of Lie type...
s.
At about the same time, it was shown that a family of five groups, called the Mathieu group
Mathieu group
In the mathematical field of group theory, the Mathieu groups, named after the French mathematician Émile Léonard Mathieu, are five finite simple groups he discovered and reported in papers in 1861 and 1873; these were the first sporadic simple groups discovered...
s and first described by Émile Léonard Mathieu
Émile Léonard Mathieu
Émile Léonard Mathieu was a French mathematician. He is most famous for his work in group theory and mathematical physics. He has given his name to the Mathieu functions, Mathieu groups and Mathieu transformation...
in 1861 and 1873, were also simple. Since these five groups were constructed by methods which did not yield infinitely many possibilities, they were called "sporadic
Sporadic group
In the mathematical field of group theory, a sporadic group is one of the 26 exceptional groups in the classification of finite simple groups. A simple group is a group G that does not have any normal subgroups except for the subgroup consisting only of the identity element, and G itself...
" by William Burnside
William Burnside
William Burnside was an English mathematician. He is known mostly as an early contributor to the theory of finite groups....
in his 1897 textbook.
Later Jordan's results on classical groups were generalized to arbitrary finite fields by Leonard Dickson, following the classification of complex simple Lie algebras by Wilhelm Killing
Wilhelm Killing
Wilhelm Karl Joseph Killing was a German mathematician who made important contributions to the theories of Lie algebras, Lie groups, and non-Euclidean geometry....
. Dickson also constructed exception groups of type G2 and E6 as well, but not of types F4, E7, or E8 . In the 1950s the work on groups of Lie type was continued, with Claude Chevalley
Claude Chevalley
Claude Chevalley was a French mathematician who made important contributions to number theory, algebraic geometry, class field theory, finite group theory, and the theory of algebraic groups...
giving a uniform construction of the classical groups and the groups of exceptional type in a 1955 paper. This omitted certain known groups (the projective unitary groups), which were obtained by "twisting" the Chevalley construction. The remaining groups of Lie type were produced by Steinberg, Tits, and Herzig (who produced 3D4(q) and 2E6(q)) and by Suzuki and Ree (the Suzuki–Ree groups).
These groups (the groups of Lie type, together with the cyclic groups, alternating groups, and the five exceptional Mathieu groups) were believed to be a complete list, but after a lull of almost a century since the work of Mathieu, in 1964 the first Janko group
Janko group
In mathematics, a Janko group is one of the four sporadic simple groups named for Zvonimir Janko. Janko constructed the first Janko group J1 in 1965. At the same time, Janko also predicted the existence of J2 and J3. In 1976, he suggested the existence of J4...
was discovered, and the remaining 20 sporadic groups were discovered or conjectured in 1965–1975, culminating in 1981, when Robert Griess announced that he had constructed Bernd Fischer
Bernd Fischer
Bernd Fischer may refer to:* Bernd Fischer , German mathematician.* Bernd Jürgen Fischer, historian and professor of history at Indiana University-Purdue University Fort Wayne....
's "Monster group
Monster group
In the mathematical field of group theory, the Monster group M or F1 is a group of finite order:...
". The Monster is the largest sporadic simple group having order of 808,017,424,794,512,875,886,459,904,961,710,757,005,754,368,000,000,000. The Monster has a faithful 196,883-dimensional representation in the 196,884-dimensional Griess algebra
Griess algebra
In mathematics, the Griess algebra is a commutative non-associative algebra on a real vector space of dimension 196884 that has the Monster group M as its automorphism group. It is named after mathematician R. L. Griess, who constructed it in 1980 and subsequently used it in 1982 to construct M...
, meaning that each element of the Monster can be expressed as a 196,883 by 196,883 matrix.
Classification
The full classification is generally accepted as starting with the Feit–Thompson theoremFeit–Thompson theorem
In mathematics, the Feit–Thompson theorem, or odd order theorem, states that every finite group of odd order is solvable. It was proved by - History : conjectured that every nonabelian finite simple group has even order...
of 1962/63, largely lasting until 1983, but only being finished in 2004.
Soon after the construction of the Monster in 1981, a proof, totaling more than 10,000 pages, was supplied that group theorists had successfully listed all finite simple groups, with victory declared in 1983 by Daniel Gorenstein. This was premature – some gaps were later discovered, notably in the classification of quasithin group
Quasithin group
In mathematics, a quasithin group is roughly a finite simple group of characteristic 2 type and width 2. Here characteristic 2 type means that its centralizers of involutions resemble those of groups of Lie type over fields of characteristic 2, and the width is roughly the maximal rank of an...
s, which were eventually replaced in 2004 by a 1,300 page classification of quasithin groups, which is now generally accepted as complete.
Tests for nonsimplicity
Sylows' test: Let n be a positive integer that is not prime, and let p be a prime divisor of n. If 1 is the only divisor of n that is equal to 1 modulo p, then there does not exist a simple group of order n.Proof: If n is a prime-power, then a group of order n has a nontrivial center
Center (group theory)
In abstract algebra, the center of a group G, denoted Z,The notation Z is from German Zentrum, meaning "center". is the set of elements that commute with every element of G. In set-builder notation,...
and, therefore, is not simple. If n is not a prime power, then every Sylow subgroup is proper, and, by Sylow's Third Theorem, we know that the number of Sylow p-subgroups of a group of order n is equal to 1 modulo p and divides n. Since 1 is the only such number, the Sylow p-subgroup is unique, and therefore it is normal. Since it is a proper, non-identity subgroup, the group is not simple.
Burnside: A non-Abelian finite simple group has order divisible by at least three distinct primes. This follows from Burnside's p-q theorem
Burnside theorem
In mathematics, Burnside's theorem in group theory states that if G is a finite group of orderp^a q^b\ where p and q are prime numbers, and a and b are non-negative integers, then G is solvable. Hence each...
.
See also
- Almost simple groupAlmost simple groupIn mathematics, a group is said to be almost simple if it contains a non-abelian simple group and is contained within the automorphism group of that simple group: if it fits between a simple group and its automorphism group.More precisely, a group is almost simple if it is isomorphic to such a group...
- Characteristically simple groupCharacteristically simple groupIn mathematics, in the field of group theory, a group is said to be characteristically simple if it has no proper nontrivial characteristic subgroups. Characteristically simple groups are sometimes also termed elementary groups...
- Quasisimple groupQuasisimple groupIn mathematics, a quasisimple group is a group that is a perfect central extension E of a simple group S...
- Semisimple group
- List of finite simple groups