Focal subgroup theorem
Encyclopedia
In abstract algebra
, the focal subgroup theorem describes the fusion of elements in a Sylow subgroup of a finite group
. The focal subgroup theorem was introduced in and is the "first major application of the transfer" according to . The focal subgroup theorem relates the ideas of transfer and fusion such as described in . Various applications of these ideas include local criteria for p-nilpotence and various non-simplicity criterion focussing on showing that a finite group has a normal subgroup
of index p.
of p-groups (respectively, elementary abelian p-groups, abelian p-groups).
Firstly, as these are weaker conditions on the groups K, one obtains the containments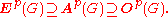
These are further related as:
Op(G) has the following alternative characterization as the subgroup generated by all Sylow q-subgroups of G as q≠p ranges over the prime divisors of the order
of G distinct from p.
Op(G) is used to define the lower p-series of G, similarly to the upper p-series described in p-core.
In other words, the "obvious" homomorphism onto an abelian p-group is in fact the most general such homomorphism.
One can define, as in the focal subgroup of H with respect to G as:
This focal subgroup measures the extent to which elements of H fuse in G, while the previous definition measured certain abelian p-group homomorphic images of the group G. The content of the focal subgroup theorem is that these two definitions of focal subgroup are compatible.
where v is the transfer homomorphism from G to P/[P,P], .
's theorem of Hall subgroup
s in order to prove similar results about the transfer into Hall π-subgroups; taking π = {p} a Hall π-subgroup is a Sylow p-subgroup, and the results of Higman are as presented above.
Interest in the hyperfocal subgroups was renewed by work of in understanding the modular representation theory
of certain well behaved blocks. The hyperfocal subgroup of P in G can defined as P∩γ∞(G) that is, as a Sylow p-subgroup of the nilpotent residual of G. If P is a Sylow p-subgroup of the finite group G, then one gets the standard focal subgroup theorem:
and the local characterization:
This compares to the local characterization of the focal subgroup as:
Puig is interested in the generalization of this situation to fusion systems, a categorical
model of the fusion pattern of a Sylow p-subgroup with respect to a finite group that also models the fusion pattern of a defect group of a p-block in modular representation theory. In fact fusion systems have found a number of surprising applications and inspirations in the area of algebraic topology
known as equivariant
homotopy theory. Some of the major algebraic theorems in this area only have topological proofs at the moment.
The choice of the family C can be made in many ways (C is what is called a "weak conjugation family" in ), and several examples are given: one can take C to be all non-identity subgroups of P, or the smaller choice of just the intersections Q = P ∩ Pg for g in G in which NP(Q) and NPg(Q) are both Sylow p-subgroups of NG(Q). The latter choice is made in . The work of studied aspects of the transfer and fusion as well, resulting in Grün's first theorem:
During the course of the Alperin–Brauer–Gorenstein theorem classifying finite simple group
s with quasi-dihedral Sylow 2-subgroups, it becomes necessary to distinguish four types of groups with quasi-dihedral Sylow 2-subgroups: the 2-nilpotent groups, the Q-type groups whose focal subgroup is a generalized quaternion group of index 2, the D-type groups whose focal subgroup a dihedral group
of index 2, and the QD-type groups whose focal subgroup is the entire quasi-dihedral group. In terms of fusion, the 2-nilpotent groups have 2 classes of involutions, and 2 classes of cyclic subgroups of order 4; the Q-type have 2 classes of involutions and one class of cyclic subgroup of order 4; the QD-type have one class each of involutions and cyclic subgroups of order 4. In other words, finite groups with quasi-dihedral Sylow 2-subgroups can be classified according to their focal subgroup, or equivalently, according to their fusion patterns. The explicit lists of groups with each fusion pattern are contained in .
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, the focal subgroup theorem describes the fusion of elements in a Sylow subgroup of a finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
. The focal subgroup theorem was introduced in and is the "first major application of the transfer" according to . The focal subgroup theorem relates the ideas of transfer and fusion such as described in . Various applications of these ideas include local criteria for p-nilpotence and various non-simplicity criterion focussing on showing that a finite group has a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of index p.
Background
The focal subgroup theorem relates several lines of investigation in finite group theory: normal subgroups of index a power of p, the transfer homomorphism, and fusion of elements.Subgroups
The following three normal subgroups of index a power of p are naturally defined, and arise as the smallest normal subgroups such that the quotient is (a certain kind of) p-group. Formally, they are kernels of the reflection onto the reflective subcategoryReflective subcategory
In mathematics, a subcategory A of a category B is said to be reflective in B when the inclusion functor from A to B has a left adjoint. This adjoint is sometimes called a reflector...
of p-groups (respectively, elementary abelian p-groups, abelian p-groups).
- Ep(G) is the intersection of all index p normal subgroups; G/Ep(G) is an elementary abelian group, and is the largest elementary abelian p-group onto which G surjects.
- Ap(G) (notation from ) is the intersection of all normal subgroups K such that G/K is an abelian p-group (i.e., K is an index
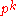normal subgroup that contains the derived group 
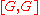): G/Ap(G) is the largest abelian p-group (not necessarily elementary) onto which G surjects. - Op(G) is the intersection of all normal subgroups K of G such that G/K is a (possibly non-abelian) p-group (i.e., K is an index
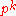normal subgroup): G/Op(G) is the largest p-group (not necessarily abelian) onto which G surjects. Op(G) is also known as the p-residual subgroup.
Firstly, as these are weaker conditions on the groups K, one obtains the containments
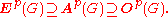These are further related as:
- Ap(G) = Op(G)[G,G].
Op(G) has the following alternative characterization as the subgroup generated by all Sylow q-subgroups of G as q≠p ranges over the prime divisors of the order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
of G distinct from p.
Op(G) is used to define the lower p-series of G, similarly to the upper p-series described in p-core.
Transfer homomorphism
The transfer homomorphism is a homomorphism that can be defined from any group G to the abelian group H/[H,H] defined by a subgroup H ≤ G of finite index, that is [G:H] < ∞. The transfer map from a finite group G into its Sylow p-subgroup has a kernel that is easy to describe:- The kernel of the transfer homomorphism from a finite group G into its Sylow p-subgroup P has Ap(G) as its kernel, .
In other words, the "obvious" homomorphism onto an abelian p-group is in fact the most general such homomorphism.
Fusion
The fusion pattern of a subgroup H in G is the equivalence relation on the elements of H where two elements h, k of H are fused if they are G-conjugate, that is, if there is some g in G such that h = kg. The normal structure of G has an effect on the fusion pattern of its Sylow p-subgroups, and conversely the fusion pattern of its Sylow p-subgroups has an effect on the normal structure of G, .Focal subgroup
If one defines, as in , the focal subgroup of P in G as the intersection P∩[G,G] of the Sylow p-subgroup P of the finite group G with the derived subgroup [G,G] of G, then the focal subgroup is clearly important as it is a Sylow p-subgroup of the derived subgroup. However, more importantly, one gets the following result:- There exists a normal subgroup K of G with G/K an abelianAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
p-groupP-groupIn mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...
isomorphic to P/P∩[G,G] (here K denotes Ap(G)), and - if K is a normal subgroup of G with G/K an abelian p-group, then P∩[G,G] ≤ K, and G/K is a homomorphic image of P/P∩[G,G], .
One can define, as in the focal subgroup of H with respect to G as:
- FocG(H) = ⟨ x−1 y x,y in H and x is G-conjugate to y ⟩.
This focal subgroup measures the extent to which elements of H fuse in G, while the previous definition measured certain abelian p-group homomorphic images of the group G. The content of the focal subgroup theorem is that these two definitions of focal subgroup are compatible.
Statement of the theorem
The focal subgroup of a finite group X with Sylow p-subgroup P is given by:- P∩[G,G] = P∩Ap(G) = P∩ker(v) = FocG(P) = ⟨ x−1 y x,y in P and x is G-conjugate to y ⟩
where v is the transfer homomorphism from G to P/[P,P], .
History and generalizations
This connection between transfer and fusion is credited to , where, in different language, the focal subgroup theorem was proved along with various generalizations. The requirement that G/K be abelian was dropped, so that Higman also studied Op(G) and the nilpotent residual γ∞(G), as so called hyperfocal subgroups. Higman also did not restrict to a single prime p, but rather allowed π-groups for sets of primes π and used Philip HallPhilip Hall
Philip Hall FRS , was an English mathematician.His major work was on group theory, notably on finite groups and solvable groups.-Biography:...
's theorem of Hall subgroup
Hall subgroup
In mathematics, a Hall subgroup of a finite group G is a subgroup whose order is coprime to its index. They are named after the group theorist Philip Hall.- Definitions :A Hall divisor of an integer n is a divisor d of n such that...
s in order to prove similar results about the transfer into Hall π-subgroups; taking π = {p} a Hall π-subgroup is a Sylow p-subgroup, and the results of Higman are as presented above.
Interest in the hyperfocal subgroups was renewed by work of in understanding the modular representation theory
Modular representation theory
Modular representation theory is a branch of mathematics, and that part of representation theory that studies linear representations of finite group G over a field K of positive characteristic...
of certain well behaved blocks. The hyperfocal subgroup of P in G can defined as P∩γ∞(G) that is, as a Sylow p-subgroup of the nilpotent residual of G. If P is a Sylow p-subgroup of the finite group G, then one gets the standard focal subgroup theorem:
- P∩γ∞(G) = P∩Op(G) = ⟨ x−1 y : x,y in P and y = xg for some g in G of order coprime to p ⟩
and the local characterization:
- P∩Op(G) = ⟨ x−1 y : x,y in Q ≤ P and y = xg for some g in NG(Q) of order coprime to p ⟩.
This compares to the local characterization of the focal subgroup as:
- P∩Ap(G) = ⟨ x−1 y : x,y in Q ≤ P and y = xg for some g in NG(Q) ⟩.
Puig is interested in the generalization of this situation to fusion systems, a categorical
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
model of the fusion pattern of a Sylow p-subgroup with respect to a finite group that also models the fusion pattern of a defect group of a p-block in modular representation theory. In fact fusion systems have found a number of surprising applications and inspirations in the area of algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
known as equivariant
Equivariant cohomology
In mathematics, equivariant cohomology is a theory from algebraic topology which applies to spaces with a group action. It can be viewed as a common generalization of group cohomology and an ordinary cohomology theory....
homotopy theory. Some of the major algebraic theorems in this area only have topological proofs at the moment.
Other characterizations
Various mathematicians have presented methods to calculate the focal subgroup from smaller groups. For instance, the influential work develops the idea of a local control of fusion, and as an example application shows that:- P ∩ Ap(G) is generated by the commutator subgroups [Q, NG(Q)] where Q varies over a family C of subgroups of P
The choice of the family C can be made in many ways (C is what is called a "weak conjugation family" in ), and several examples are given: one can take C to be all non-identity subgroups of P, or the smaller choice of just the intersections Q = P ∩ Pg for g in G in which NP(Q) and NPg(Q) are both Sylow p-subgroups of NG(Q). The latter choice is made in . The work of studied aspects of the transfer and fusion as well, resulting in Grün's first theorem:
- P ∩ Ap(G) is generated by P∩[N,N] and P ∩ [Q, Q] where N = NG(P) and Q ranges over the set of Sylow p-subgroups Q = Pg of G .
Applications
The textbook presentations in , , , , all contain various applications of the focal subgroup theorem relating fusion, transfer, and a certain kind of splitting called p-nilpotence.During the course of the Alperin–Brauer–Gorenstein theorem classifying finite simple group
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
s with quasi-dihedral Sylow 2-subgroups, it becomes necessary to distinguish four types of groups with quasi-dihedral Sylow 2-subgroups: the 2-nilpotent groups, the Q-type groups whose focal subgroup is a generalized quaternion group of index 2, the D-type groups whose focal subgroup a dihedral group
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
of index 2, and the QD-type groups whose focal subgroup is the entire quasi-dihedral group. In terms of fusion, the 2-nilpotent groups have 2 classes of involutions, and 2 classes of cyclic subgroups of order 4; the Q-type have 2 classes of involutions and one class of cyclic subgroup of order 4; the QD-type have one class each of involutions and cyclic subgroups of order 4. In other words, finite groups with quasi-dihedral Sylow 2-subgroups can be classified according to their focal subgroup, or equivalently, according to their fusion patterns. The explicit lists of groups with each fusion pattern are contained in .