
Proper map
Encyclopedia
In mathematics
, a continuous function
between topological space
s is called proper if inverse images of compact subsets
are compact. In algebraic geometry
, the analogous concept is called a proper morphism.
f : X → Y between two topological space
s is proper if and only if the preimage of every compact
set in Y is compact in X.
There are several competing descriptions. For instance, a continuous map f is proper if it is a closed map and the pre-image of every point in Y is compact. For a proof of this fact see the end of this section. More abstractly, f is proper if for any space Z the map
is closed. These definitions are equivalent to the previous one if X is Hausdorff
and Y is locally compact
Hausdorff.
An equivalent, possibly more intuitive definition is as follows: we say an infinite sequence of points {pi} in a topological space X escapes to infinity if, for every compact set S ⊂ X only finitely many points pi are in S. Then a map f : X → Y is proper if and only if for every sequence of points {pi} that escapes to infinity in X, {f(pi)} escapes to infinity in Y.
(This equivalent definition may need some more restrictions like f is continuous. Otherwise, it is invalid, i.e. one can not deduce properness from a sequence which escapes to infinity maps to a sequence which escapes to infinity in Y.)
 be a continuous closed map, such that
be a continuous closed map, such that 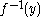 is compact (in X) for all
is compact (in X) for all 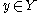 . Let
. Let 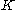 be a compact subset of
be a compact subset of 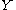 . We will show that
. We will show that 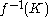 is compact.
is compact.
Let be an open cover of
be an open cover of 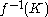 . Then for all
. Then for all 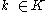 this is also an open cover of
this is also an open cover of 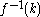 . Since the latter is assumed to be compact, it has a finite subcover. In other words, for all
. Since the latter is assumed to be compact, it has a finite subcover. In other words, for all 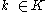 there is a finite set
there is a finite set 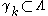 such that
such that 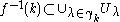 .
.
The set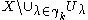 is closed. Its image is closed in Y, because f is a closed map. Hence the set
is closed. Its image is closed in Y, because f is a closed map. Hence the set
 is open in Y. It is easy to check that
is open in Y. It is easy to check that 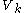 contains the point
contains the point 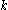 .
.
Now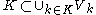 and because K is assumed to be compact, there are finitely many points
and because K is assumed to be compact, there are finitely many points  such that
such that 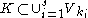 . Furthermore the set
. Furthermore the set 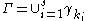 is a finite union of finite sets, thus
is a finite union of finite sets, thus 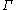 is finite.
is finite.
Now it follows that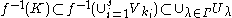 and we have found a finite subcover of
and we have found a finite subcover of 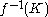 , which completes the proof.
, which completes the proof.
the notion of proper maps of topological spaces to locales
and topoi
, see .
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
between topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s is called proper if inverse images of compact subsets
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
are compact. In algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, the analogous concept is called a proper morphism.
Definition
A functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f : X → Y between two topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s is proper if and only if the preimage of every compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
set in Y is compact in X.
There are several competing descriptions. For instance, a continuous map f is proper if it is a closed map and the pre-image of every point in Y is compact. For a proof of this fact see the end of this section. More abstractly, f is proper if for any space Z the map
- f × idZ: X × Z → Y × Z
is closed. These definitions are equivalent to the previous one if X is Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
and Y is locally compact
Locally compact space
In topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space.-Formal definition:...
Hausdorff.
An equivalent, possibly more intuitive definition is as follows: we say an infinite sequence of points {pi} in a topological space X escapes to infinity if, for every compact set S ⊂ X only finitely many points pi are in S. Then a map f : X → Y is proper if and only if for every sequence of points {pi} that escapes to infinity in X, {f(pi)} escapes to infinity in Y.
(This equivalent definition may need some more restrictions like f is continuous. Otherwise, it is invalid, i.e. one can not deduce properness from a sequence which escapes to infinity maps to a sequence which escapes to infinity in Y.)
Proof of fact
Let be a continuous closed map, such that
be a continuous closed map, such that 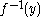 is compact (in X) for all
is compact (in X) for all 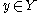 . Let
. Let 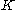 be a compact subset of
be a compact subset of 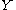 . We will show that
. We will show that 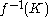 is compact.
is compact.Let
 be an open cover of
be an open cover of 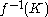 . Then for all
. Then for all 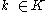 this is also an open cover of
this is also an open cover of 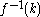 . Since the latter is assumed to be compact, it has a finite subcover. In other words, for all
. Since the latter is assumed to be compact, it has a finite subcover. In other words, for all 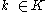 there is a finite set
there is a finite set 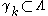 such that
such that 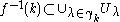 .
.The set
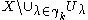 is closed. Its image is closed in Y, because f is a closed map. Hence the set
is closed. Its image is closed in Y, because f is a closed map. Hence the set is open in Y. It is easy to check that
is open in Y. It is easy to check that 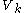 contains the point
contains the point 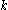 .
.Now
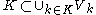 and because K is assumed to be compact, there are finitely many points
and because K is assumed to be compact, there are finitely many points  such that
such that 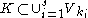 . Furthermore the set
. Furthermore the set 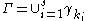 is a finite union of finite sets, thus
is a finite union of finite sets, thus 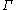 is finite.
is finite.Now it follows that
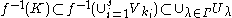 and we have found a finite subcover of
and we have found a finite subcover of 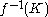 , which completes the proof.
, which completes the proof.Properties
- A topological space is compact if and only if the map from that space to a single point is proper.
- Every continuous map from a compact space to a Hausdorff spaceHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
is both proper and closed. - If f : X → Y is a proper continuous map and Y is a compactly generated Hausdorff space (this includes Hausdorff spaces which are either first-countable or locally compact), then f is closed.
Generalization
It is possible to generalizethe notion of proper maps of topological spaces to locales
Pointless topology
In mathematics, pointless topology is an approach to topology that avoids mentioning points. The name 'pointless topology' is due to John von Neumann...
and topoi
Topos
In mathematics, a topos is a type of category that behaves like the category of sheaves of sets on a topological space...
, see .

