
Oscillation (mathematics)
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, oscillation is the behaviour of a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s or a real-valued function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, which does not converge, but also does not diverge
Divergent series
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....
to +∞ or −∞; that is, oscillation is the failure to have a limit
Limit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
, and is also a quantitative measure for that.
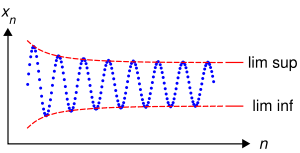
Oscillation is defined as the difference (possibly ∞) between the limit superior and limit inferior
Limit superior and limit inferior
In mathematics, the limit inferior and limit superior of a sequence can be thought of as limiting bounds on the sequence...
. It is undefined if both are +∞ or both are −∞ (that is, if the difference between the superior and inferior limits of the sequence or function is in one of the indeterminate forms +∞ + (-∞) or -∞ - (-∞)). For a sequence, the oscillation is defined at infinity, it is zero if and only if the sequence converges. For a function, the oscillation is defined at every limit point
Limit point
In mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
in (−∞, +∞) of the domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
of the function (apart from the mentioned restriction). It is zero at a point if and only if the function has a finite limit
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
at that point.
Examples

- 1/x has oscillation ∞ at x = 0, and oscillation 0 at other finite x and at −∞ and +∞.
- sin (1/x) (the topologist's sine curveTopologist's sine curveIn the branch of mathematics known as topology, the topologist's sine curve is a topological space with several interesting properties that make it an important textbook example....
) has oscillation 2 at x = 0, and 0 elsewhere. - sin x has oscillation 0 at every finite x, and 2 at −∞ and +∞.
- The sequence 1, −1, 1, −1, 1, −1, ... has oscillation 2.
In the last example the sequence is periodic
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
, and any sequence that is periodic without being constant will have non-zero oscillation. However, non-zero oscillation does not usually indicate periodicity.
Geometrically, the graph of an oscillating function on the real numbers follows some path in the xy-plane, without settling into ever-smaller regions. In well-behaved
Well-behaved
Mathematicians very frequently speak of whether a mathematical object — a function, a set, a space of one sort or another — is "well-behaved" or not. The term has no fixed formal definition, and is dependent on mathematical interests, fashion, and taste...
cases the path might look like a loop coming back on itself, that is, periodic behaviour; in the worst cases quite irregular movement covering a whole region.
Continuity
Oscillation can be used to define continuity of a functionContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, and is easily equivalent to the usual ε-δ definition (in the case of functions defined everywhere on the real line): a function ƒ is continuous at a point x0 if and only if the oscillation is zero; in symbols,
 A benefit of this definition is that it quantifies discontinuity: the oscillation gives how much the function is discontinuous at a point.
A benefit of this definition is that it quantifies discontinuity: the oscillation gives how much the function is discontinuous at a point.For example, in the classification of discontinuities
Classification of discontinuities
Continuous functions are of utmost importance in mathematics and applications. However, not all functions are continuous. If a function is not continuous at a point in its domain, one says that it has a discontinuity there...
:
- in a removable discontinuity, the distance that the value of the function is off by is the oscillation;
- in a jump discontinuity, the size of the jump is the oscillation (assuming that the value at the point lies between these limits from the two sides);
- in an essential discontinuity, oscillation measures the failure of a limit to exist.
This definition is useful in descriptive set theory
Descriptive set theory
In mathematical logic, descriptive set theory is the study of certain classes of "well-behaved" subsets of the real line and other Polish spaces...
to study the set of discontinuities and continuous points – the continuous points are the intersection of the sets where the oscillation is less than ε (hence a Gδ set
G-delta set
In the mathematical field of topology, a Gδ set is a subset of a topological space that is a countable intersection of open sets. The notation originated in Germany with G for Gebiet meaning open set in this case and δ for Durchschnitt .The term inner limiting set is also used...
) – and gives a very quick proof of one direction of the Lebesgue integrability condition.
The oscillation is equivalence to the ε-δ definition by a simple re-arrangement, and by using a limit (lim sup, lim inf) to define oscillation: if (at a given point) for a given ε0 there is no δ that satisfies the ε-δ definition, then the oscillation is at least ε0, and conversely if for every ε there is a desired δ, the oscillation is 0. The oscillation definition can be naturally generalized to maps from a topological space to a metric space.
Generalizations
More generally, if f : X → Y is a function from a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X into a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
Y, then the oscillation of f is defined at each x ∈ X by


