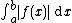In calculus

Calculus

Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...

, an improper integral is the limit

Limit (mathematics)

In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...

 of a definite integral as an endpoint of the interval of integration approaches either a specified real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

 or ∞ or −∞ or, in some cases, as both endpoints approach limits.

Specifically, an improper integral is a limit of the form
or of the form
in which one takes a limit in one or the other (or sometimes both) endpoints . Integrals are also improper if the integrand is undefined at an interior point of the domain of integration, or at multiple such points.

It is often necessary to use improper integrals in order to compute a value for integrals which may not exist in the conventional sense (as a Riemann integral

Riemann integral

In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...

, for instance) because of a singularity in the function, or an infinite endpoint of the domain of integration.

Examples

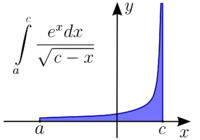
The following integral does not exist as a Riemann integral

Riemann integral

In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...

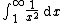
because the domain of integration is unbounded. (The Riemann integral is only well-defined over a bounded domain.) However, it may be assigned a value as an improper integral by interpreting it instead as a limit


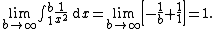
The following integral also fails to exist as a Riemann integral:


Here the function is unbounded, and the Riemann integral is not well-defined for unbounded functions. However, if the integral is instead understood as the limit:


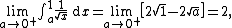
then the limit converges.

Convergence of the integral

An improper integral converges if the limit defining it exists. Thus for example one says that the improper integral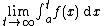
exists and is equal to L if the integrals under the limit exist for all sufficiently large t, and the value of the limit is equal to L.

It is also possible for an improper integral to diverge to infinity. In that case, one may assign the value of ∞ (or −∞) to the integral. For instance
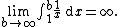
However, other improper integrals may simply diverge in no particular direction, such as
which does not exist, even as an extended real number.

A limitation of the technique of improper integration is that the limit must be taken with respect to one endpoint at a time. Thus, for instance, an improper integral of the form


is defined by taking two separate limits; to wit


provided the double limit is finite. By the properties of the integral, this can also be written as a pair of distinct improper integrals of the first kind:


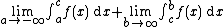
where c is any convenient point at which to start the integration.

It is sometimes possible to define improper integrals where both endpoints are infinite, such as the Gaussian integral

Gaussian integral

The Gaussian integral, also known as the Euler-Poisson integral or Poisson integral, is the integral of the Gaussian function e−x2 over the entire real line.It is named after the German mathematician and...

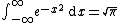 . But one cannot even define other integrals of this kind unambiguously, such as 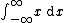, since the double limit diverges: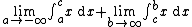


In this case, one can however define an improper integral in the sense of Cauchy principal value

Cauchy principal value

In mathematics, the Cauchy principal value, named after Augustin Louis Cauchy, is a method for assigning values to certain improper integrals which would otherwise be undefined.-Formulation:...

:


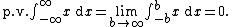
The questions one must address in determining an improper integral are:

• Does the limit exist?
• Can the limit be computed?

The first question is an issue of mathematical analysis

Mathematical analysis

Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...

. The second one can be addressed by calculus techniques, but also in some cases by contour integration, Fourier transform

Fourier transform

In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...

s and other more advanced methods.

Types of integrals

There is more than one theory of integration

Integral

Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...

. From the point of view of calculus, the Riemann integral

Riemann integral

In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...

 theory is usually assumed as the default theory. In using improper integrals, it can matter which integration theory is in play.

• For the Darboux integral
  Darboux integral
  In real analysis, a branch of mathematics, the Darboux integral or Darboux sum is one possible definition of the integral of a function. Darboux integrals are equivalent to Riemann integrals, meaning that a function is Darboux-integrable if and only if it is Riemann-integrable, and the values of...
  
  , improper integration is necessary both for unbounded intervals (since one cannot divide the interval into finitely many subintervals of finite length) and for unbounded functions with finite integral (since, supposing it is unbounded above, then the upper integral will be infinite, but the lower integral will be finite).
• For the Riemann integral
  Riemann integral
  In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
  
  , improper integration is also necessary for unbounded intervals and for unbounded functions, as with the Darboux integral
  Darboux integral
  In real analysis, a branch of mathematics, the Darboux integral or Darboux sum is one possible definition of the integral of a function. Darboux integrals are equivalent to Riemann integrals, meaning that a function is Darboux-integrable if and only if it is Riemann-integrable, and the values of...
  
  .
• The Lebesgue integral deals differently with unbounded domains and unbounded functions, so that often an integral which only exists as an improper Riemann integral will exist as a (proper) Lebesgue integral, such as 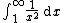. On the other hand, there are also integrals that have an improper Riemann integral but do not have a (proper) Lebesgue integral, such as . The Lebesgue theory does not see this as a deficiency: from the point of view of measure theory, 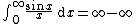and cannot be defined satisfactorily. In some situations, however, it may be convenient to employ improper Lebesgue integrals as is the case, for instance, when defining the Cauchy principal value
  Cauchy principal value
  In mathematics, the Cauchy principal value, named after Augustin Louis Cauchy, is a method for assigning values to certain improper integrals which would otherwise be undefined.-Formulation:...
  
  .
• For the Henstock–Kurzweil integral, improper integration is not necessary, and this is seen as a strength of the theory: it encompasses all Lebesgue integrable and improper Riemann integrable functions.

Improper Riemann integrals and Lebesgue integrals

In some cases, the integral


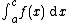
can be defined as an integral (a Lebesgue integral, for instance) without reference to the limit


but cannot otherwise be conveniently computed. This often happens when the function f being integrated from a to c has a vertical asymptote at c, or if c = ∞ (see Figures 1 and 2). In such cases, the improper Riemann integral allows one to calculate the Lebesgue integral of the function. Specifically, the following theorem holds :

• If a function f is Riemann integrable on [a,b] for every b ≥ a, and the partial integrals

are bounded as b → ∞, then the improper Riemann integrals

both exist. Furthermore, f is Lebesgue integrable on [a, ∞), and its Lebesgue integral is equal to its improper Riemann integral.

For example, the integral
can be interpreted alternatively as the improper integral
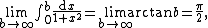
or it may be interpreted instead as a Lebesgue integral over the set (0, ∞). Since both of these kinds of integral agree, one is free to choose the first method to calculate the value of the integral, even if one ultimately wishes to regard it as a Lebesgue integral. Thus improper integrals are clearly useful tools for obtaining the actual values of integrals.

In other cases, however, the integral from a to c is not even defined, because the integrals of the positive and negative parts of f(x) \mathrm{d}x from a to c are both infinite, but nonetheless the limit may exist. Such cases are "properly improper" integrals, i.e. their values cannot be defined except as such limits. For example,


cannot be interpreted as a Lebesgue integral, since


This is therefore a "properly" improper integral, whose value is given by

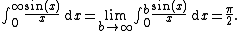
Singularities

One can speak of the singularities of an improper integral, meaning those points of the extended real number line

Extended real number line

In mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...

 at which limits are used.

Such an integral is often written symbolically just like a standard definite integral, perhaps with infinity as a limit of integration. But that conceals the limiting process. By using the more advanced Lebesgue integral, rather than the Riemann integral, one can in some cases bypass this requirement, but if one simply wants to evaluate the limit to a definite answer, that technical fix may not necessarily help. It is more or less essential in the theoretical treatment for the Fourier transform, with pervasive use of integrals over the whole real line.

Cauchy principal value

Consider the difference in values of two limits: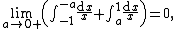



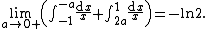
The former is the Cauchy principal value of the otherwise ill-defined expression


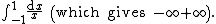
Similarly, we have


but


The former is the principal value of the otherwise ill-defined expression


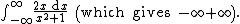
All of the above limits are cases of the indeterminate form

Indeterminate form

In calculus and other branches of mathematical analysis, an indeterminate form is an algebraic expression obtained in the context of limits. Limits involving algebraic operations are often performed by replacing subexpressions by their limits; if the expression obtained after this substitution...

 ∞ − ∞.

These pathologies

Pathological (mathematics)

In mathematics, a pathological phenomenon is one whose properties are considered atypically bad or counterintuitive; the opposite is well-behaved....

 do not affect "Lebesgue-integrable" functions, that is, functions the integrals of whose absolute value

Absolute value

In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...

s are finite.

Summability

An indefinite integral may diverge in the sense that the limit defining it may not exist. In this case, there are more sophisticated definitions of the limit which can produce a convergent value for the improper integral. These are called summability methods.

One summability method, popular in Fourier analysis, is that of Cesàro summation

Cesàro summation

In mathematical analysis, Cesàro summation is an alternative means of assigning a sum to an infinite series. If the series converges in the usual sense to a sum A, then the series is also Cesàro summable and has Cesàro sum A...

. The integral


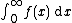
is Cesàro summable (C, α) if


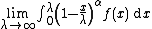
exists and is finite . The value of this limit, should it exist, is the (C, α) sum of the integral.

An integral is (C, 0) summable precisely when it exists as an improper integral. However, there are integrals which are (C, α) summable for α > 0 which fail to converge as improper integrals (in the sense of Riemann or Lebesgue). One example is the integral


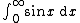
which fails to exist as an improper integral, but is (C,α) summable for every α > 0, with value 1. This is an integral version of Grandi's series.

External links

• Numerical Methods to Solve Improper Integrals at Holistic Numerical Methods Institute
• Improper integrals -- chapter from an online textbook