Jordan measure
Encyclopedia
In mathematics
, the Peano–Jordan measure (also known as the Jordan content) is an extension of the notion of size (length
, area, volume
) to shapes more complicated than, for example, a triangle
, disk
, or parallelepiped
.
It turns out that for a set to have Jordan measure it should be well-behaved
in a certain restrictive sense. For this reason, it is now more common to work with the Lebesgue measure
, which is an extension of the Jordan measure to a larger class of sets. Historically speaking, the Jordan measure came first, towards the end of the nineteenth century.
The Jordan measure is named after its originators, the French
mathematician
Camille Jordan
, and the Italian
mathematician
Giuseppe Peano
.
Rn. One starts by considering products of bounded
intervals
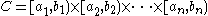
which are closed at the left end and open at the right end (half-open intervals is a technical choice; as we see below, one can use closed or open intervals if preferred). Such a set will be called a n-dimensional rectangle, or simply a rectangle. One defines the Jordan measure of such a rectangle to be the product of the lengths of the intervals:
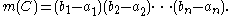
Next, one considers simple sets, sometimes called polyrectangles, which are finite unions
of rectangles,
for any k≥1. One cannot define the Jordan measure of S as simply the sum of the measures of the individual rectangles, because such a representation of S is far from unique, and there could be significant overlaps between the rectangles. Luckily, any such simple set S can be rewritten as a union of another finite family of rectangles, rectangles which this time are mutually disjoint, and then one defines the Jordan measure m(S) as the sum of measures of the disjoint rectangles. One can show that this definition of the Jordan measure of S is independent of the representation of S as a finite union of disjoint rectangles. It is in the "rewriting" step that the assumption of rectangles being made of half-open intervals is used.
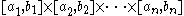
is not a simple set, and neither is a ball
. Thus, so far the set of Jordan measurable sets is still very limited. The key step is then defining a bounded set to be Jordan measurable if it is "well-approximated" by simple sets, exactly in the same way as a function is Riemann integrable
if it is well-approximated by piecewise-constant functions.
Formally, for a bounded set B, define its inner Jordan measure as
and its outer measure as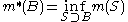
where the infimum
and supremum are taken over simple sets S. The set B is said to be Jordan measurable if the inner measure of B equals the outer measure. The common value of the two measures is then simply called the Jordan measure of B.
It turns out that all rectangles (open or closed), as well all balls, simplex
es, etc., are Jordan measurable. Also, if one considers two continuous function
s, the set of points between the graphs of those functions is Jordan measurable as long as that set is bounded and the common domain of the two functions is Jordan measurable. Any finite union and intersection of Jordan measurable sets is Jordan measurable, as well as the set difference of any two Jordan measurable sets. A compact set is not necessarily Jordan measurable. For example, the fat Cantor set is not. Its inner Jordan measure vanishes, since its complement
is dense
; however, its outer Jordan measure does not vanish, since it cannot be less than (in fact, is equal to) its Lebesgue measure. Also, a bounded open set
is not necessarily Jordan measurable. For example, the complement of the fat Cantor set (within the interval) is not. A bounded set is Jordan measurable if and only if its indicator function is Riemann-integrable
.http://planetmath.org/encyclopedia/Volume.html
Equivalently, for a bounded set B the inner Jordan measure of B is the Lebesgue measure of the interior
of B and the outer Jordan measure is the Lebesgue measure of the closure
. From this it follows that a bounded set is Jordan measurable if and only if its boundary
has Lebesgue measure zero. (Or equivalently, if the boundary has Jordan measure zero; the equivalence holds due to compactness of the boundary.)
s contained in the interval [0,1] is then not Jordan measurable, as its boundary is [0,1] which is not of Jordan measure zero. Intuitively however, the set of rational numbers is a "small" set, as it is countable, and it should have "size" zero. That is indeed true, but only if one replaces the Jordan measure with the Lebesgue measure
. The Lebesgue measure of a set is the same as its Jordan measure as long as that set has a Jordan measure. However, the Lebesgue measure is defined for a much wider class of sets, like the set of rational numbers in an interval mentioned earlier, and also for sets which may be unbounded or fractals. Also, the Lebesgue measure, unlike the Jordan measure, is a true measure
, that is, any countable union of Lebesgue measurable sets is Lebesgue measurable, whereas countable unions of Jordan measurable sets need not be Jordan measurable.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Peano–Jordan measure (also known as the Jordan content) is an extension of the notion of size (length
Length
In geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire...
, area, volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
) to shapes more complicated than, for example, a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
, disk
Disk (mathematics)
In geometry, a disk is the region in a plane bounded by a circle.A disk is said to be closed or open according to whether or not it contains the circle that constitutes its boundary...
, or parallelepiped
Parallelepiped
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts...
.
It turns out that for a set to have Jordan measure it should be well-behaved
Well-behaved
Mathematicians very frequently speak of whether a mathematical object — a function, a set, a space of one sort or another — is "well-behaved" or not. The term has no fixed formal definition, and is dependent on mathematical interests, fashion, and taste...
in a certain restrictive sense. For this reason, it is now more common to work with the Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
, which is an extension of the Jordan measure to a larger class of sets. Historically speaking, the Jordan measure came first, towards the end of the nineteenth century.
The Jordan measure is named after its originators, the French
France
The French Republic , The French Republic , The French Republic , (commonly known as France , is a unitary semi-presidential republic in Western Europe with several overseas territories and islands located on other continents and in the Indian, Pacific, and Atlantic oceans. Metropolitan France...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Camille Jordan
Camille Jordan
Marie Ennemond Camille Jordan was a French mathematician, known both for his foundational work in group theory and for his influential Cours d'analyse. He was born in Lyon and educated at the École polytechnique...
, and the Italian
Italy
Italy , officially the Italian Republic languages]] under the European Charter for Regional or Minority Languages. In each of these, Italy's official name is as follows:;;;;;;;;), is a unitary parliamentary republic in South-Central Europe. To the north it borders France, Switzerland, Austria and...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Giuseppe Peano
Giuseppe Peano
Giuseppe Peano was an Italian mathematician, whose work was of philosophical value. The author of over 200 books and papers, he was a founder of mathematical logic and set theory, to which he contributed much notation. The standard axiomatization of the natural numbers is named the Peano axioms in...
.
Jordan measure of "simple sets"
Consider the Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn. One starts by considering products of bounded
Bounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
intervals
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
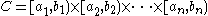
which are closed at the left end and open at the right end (half-open intervals is a technical choice; as we see below, one can use closed or open intervals if preferred). Such a set will be called a n-dimensional rectangle, or simply a rectangle. One defines the Jordan measure of such a rectangle to be the product of the lengths of the intervals:
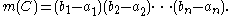
Next, one considers simple sets, sometimes called polyrectangles, which are finite unions
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of rectangles,
for any k≥1. One cannot define the Jordan measure of S as simply the sum of the measures of the individual rectangles, because such a representation of S is far from unique, and there could be significant overlaps between the rectangles. Luckily, any such simple set S can be rewritten as a union of another finite family of rectangles, rectangles which this time are mutually disjoint, and then one defines the Jordan measure m(S) as the sum of measures of the disjoint rectangles. One can show that this definition of the Jordan measure of S is independent of the representation of S as a finite union of disjoint rectangles. It is in the "rewriting" step that the assumption of rectangles being made of half-open intervals is used.
Extension to more complicated sets
Notice that a set which is a product of closed intervals,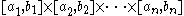
is not a simple set, and neither is a ball
Ball (mathematics)
In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
. Thus, so far the set of Jordan measurable sets is still very limited. The key step is then defining a bounded set to be Jordan measurable if it is "well-approximated" by simple sets, exactly in the same way as a function is Riemann integrable
Riemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
if it is well-approximated by piecewise-constant functions.
Formally, for a bounded set B, define its inner Jordan measure as

and its outer measure as
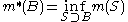
where the infimum
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
and supremum are taken over simple sets S. The set B is said to be Jordan measurable if the inner measure of B equals the outer measure. The common value of the two measures is then simply called the Jordan measure of B.
It turns out that all rectangles (open or closed), as well all balls, simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
es, etc., are Jordan measurable. Also, if one considers two continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s, the set of points between the graphs of those functions is Jordan measurable as long as that set is bounded and the common domain of the two functions is Jordan measurable. Any finite union and intersection of Jordan measurable sets is Jordan measurable, as well as the set difference of any two Jordan measurable sets. A compact set is not necessarily Jordan measurable. For example, the fat Cantor set is not. Its inner Jordan measure vanishes, since its complement
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
is dense
Dense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
; however, its outer Jordan measure does not vanish, since it cannot be less than (in fact, is equal to) its Lebesgue measure. Also, a bounded open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
is not necessarily Jordan measurable. For example, the complement of the fat Cantor set (within the interval) is not. A bounded set is Jordan measurable if and only if its indicator function is Riemann-integrable
Riemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
.http://planetmath.org/encyclopedia/Volume.html
Equivalently, for a bounded set B the inner Jordan measure of B is the Lebesgue measure of the interior
Interior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
of B and the outer Jordan measure is the Lebesgue measure of the closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
. From this it follows that a bounded set is Jordan measurable if and only if its boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
has Lebesgue measure zero. (Or equivalently, if the boundary has Jordan measure zero; the equivalence holds due to compactness of the boundary.)
The Lebesgue measure
This last property greatly limits the types of sets which are Jordan measurable. For example, the set of rational numberRational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s contained in the interval [0,1] is then not Jordan measurable, as its boundary is [0,1] which is not of Jordan measure zero. Intuitively however, the set of rational numbers is a "small" set, as it is countable, and it should have "size" zero. That is indeed true, but only if one replaces the Jordan measure with the Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
. The Lebesgue measure of a set is the same as its Jordan measure as long as that set has a Jordan measure. However, the Lebesgue measure is defined for a much wider class of sets, like the set of rational numbers in an interval mentioned earlier, and also for sets which may be unbounded or fractals. Also, the Lebesgue measure, unlike the Jordan measure, is a true measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
, that is, any countable union of Lebesgue measurable sets is Lebesgue measurable, whereas countable unions of Jordan measurable sets need not be Jordan measurable.