In
mathematicsMathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an
indicator function or a
characteristic function is a
functionIn mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
defined on a set
that indicates membership of an element in a
subsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of
, having the value 1 for all elements of
A and the value 0 for all elements of
X not in
A.
Definition
The indicator function of a subset
of a set
is a function
defined as
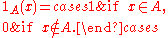
The
Iverson bracket allows the equivalent notation,
, to be used instead of
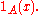
The function
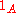is sometimes denoted
or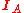
or even just
. (The
Greek letterThe Greek alphabet is the script that has been used to write the Greek language since at least 730 BC . The alphabet in its classical and modern form consists of 24 letters ordered in sequence from alpha to omega...
χ appears because it is the initial letter of the Greek word
characteristic.)
Remark on notation and terminology
- The notation
may signify the identity functionIn mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
.
- The notation
may signify the characteristic functionIn the field of mathematics known as convex analysis, the characteristic function of a set is a convex function that indicates the membership of a given element in that set...
in convex analysisConvex analysis is the branch of mathematics devoted to the study of properties of convex functions and convex sets, often with applications in convex minimization, a subdomain of optimization theory....
.
A related concept in
statisticsStatistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
is that of a dummy variable (this must not be confused with "dummy variables" as that term is usually used in mathematics, also called a
bound variableIn mathematics, and in other disciplines involving formal languages, including mathematical logic and computer science, a free variable is a notation that specifies places in an expression where substitution may take place...
).
The term "
characteristic functionIn mathematics, characteristic function can refer to any of several distinct concepts:* The most common and universal usage is as a synonym for indicator function, that is the function* In probability theory, the characteristic function of any probability distribution on the real line is given by...
" has an unrelated meaning in
probability theoryProbability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
. For this reason, probabilists use the term
indicator function for the function defined here almost exclusively, while mathematicians in other fields are more likely to use the term
characteristic function to describe the function which indicates membership in a set.
Basic properties
The
indicator or
characteristic function of a subset
of some set
, maps elements of
to the range
.
This mapping is surjective only when
is a non-empty proper subset of
. If
, then
. By a similar argument, if
then
.
In the following, the dot represents multiplication, 1·1 = 1, 1·0 = 0 etc. "+" and "−" represent addition and subtraction. "
" and "
" is intersection and union, respectively.
If
and
are two subsets of
, then
and the indicator function of the
complementIn set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of A i.e. A
C is:
More generally, suppose
is a collection of subsets of
. For any
,
is clearly a product of
s and
s. This product has the value 1 at
precisely those
which belong to none of the sets
and
is
otherwise. That is
Expanding the product on the left hand side,
-
where
is the cardinality of
. This is one form of the principle of inclusion-exclusion.
As suggested by the previous example, the indicator function is a useful notational device in
combinatoricsCombinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
. The notation is used in other places as well, for instance in
probability theoryProbability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
: if
is a
probability spaceIn probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
with probability measure
and
is a
measurable setIn mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
, then
becomes a
random variableIn probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
whose
expected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
is equal to the probability of
This identity is used in a simple proof of
Markov's inequalityIn probability theory, Markov's inequality gives an upper bound for the probability that a non-negative function of a random variable is greater than or equal to some positive constant...
.
In many cases, such as
order theoryOrder theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
, the inverse of the indicator function may be defined. This is commonly called the generalized Möbius function, as a generalization of the inverse of the indicator function in elementary
number theoryNumber theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the
Möbius functionThe classical Möbius function μ is an important multiplicative function in number theory and combinatorics. The German mathematician August Ferdinand Möbius introduced it in 1832...
. (See paragraph below about the use of the inverse in classical recursion theory.)
Mean, variance and covariance
Given a
probability spaceIn probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
with
, the indicator random variable
is defined by
if
otherwise
- Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
: 
- Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
: 
- Covariance
In probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
: 
Characteristic function in recursion theory, Gödel's and Kleene's representing function
Kurt GödelKurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
described the
representing function in his 1934 paper "On Undecidable Propositions of Formal Mathematical Systems". (The paper appears on pp. 41-74 in
Martin DavisMartin David Davis, is an American mathematician, known for his work on Hilbert's tenth problem . He received his Ph.D. from Princeton University in 1950, where his adviser was Alonzo Church . He is Professor Emeritus at New York University. He is the co-inventor of the Davis-Putnam and the DPLL...
ed.
The Undecidable):
- "There shall correspond to each class or relation R a representing function φ(x1, . . ., xn) = 0 if R(x1, . . ., xn) and φ(x1, . . ., xn)=1 if ~R(x1, . . ., xn)." (p. 42; the "~" indicates logical inversion i.e. "NOT")
Stephen Kleene (1952) (p. 227) offers up the same definition in the context of the
primitive recursive functionThe primitive recursive functions are defined using primitive recursion and composition as central operations and are a strict subset of the total µ-recursive functions...
s as a function φ of a predicate P, takes on values 0 if the predicate is true and 1 if the predicate is false.
For example, because the product of characteristic functions φ
1*φ
2* . . . *φ
n = 0 whenever any one of the functions equals 0, it plays the role of logical OR: IF φ
1=0 OR φ
2=0 OR . . . OR φ
n=0 THEN their product is 0. What appears to the modern reader as the representing function's logical-inversion, i.e. the representing function is 0 when the function R is "true" or satisfied", plays a useful role in Kleene's definition of the logical functions OR, AND, and IMPLY (p. 228), the bounded- (p. 228) and unbounded- (p. 279ff)
mu operatorIn computability theory, the μ operator, minimization operator, or unbounded search operator searches for the least natural number with a given property.- Definition :...
s (Kleene (1952)) and the CASE function (p. 229).
Characteristic function in fuzzy set theory
In classical mathematics, characteristic functions of sets only take values 1 (members) or 0 (non-members). In fuzzy set theory, characteristic functions are generalized to take value in the real unit interval [0, 1], or more generally, in some
algebraUniversal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
or
structureIn universal algebra and in model theory, a structure consists of a set along with a collection of finitary operations and relations which are defined on it....
(usually required to be at least a
posetIn mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
or
latticeIn mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
). Such generalized characteristic functions are more usually called
membership functionThe membership function of a fuzzy set is a generalization of the indicator function in classical sets. In fuzzy logic, it represents the degree of truth as an extension of valuation. Degrees of truth are often confused with probabilities, although they are conceptually distinct, because fuzzy...
s, and the corresponding "sets" are called
fuzzy sets. Fuzzy sets model the gradual change in the membership
degree seen in many real-world predicates like "tall", "warm", etc.
See also
- Dirac delta
- Extension (predicate logic)
The extension of a predicatea truth-valued functionis the set of tuples of values that, used as arguments, satisfy the predicate. Such a set of tuples is a relation.For example the statement "d2 is the weekday following d1"...
- Free variables and bound variables
In mathematics, and in other disciplines involving formal languages, including mathematical logic and computer science, a free variable is a notation that specifies places in an expression where substitution may take place...
- Heaviside step function
The Heaviside step function, or the unit step function, usually denoted by H , is a discontinuous function whose value is zero for negative argument and one for positive argument....
- Iverson bracket
- Kronecker delta, a function that can be viewed as an indicator for the identity relation
- Multiset
In mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
- Membership function
The membership function of a fuzzy set is a generalization of the indicator function in classical sets. In fuzzy logic, it represents the degree of truth as an extension of valuation. Degrees of truth are often confused with probabilities, although they are conceptually distinct, because fuzzy...
- Simple function
In the mathematical field of real analysis, a simple function is a real-valued function over a subset of the real line which attains only a finite number of values...