Pseudovector
Encyclopedia
In physics
and mathematics
, a pseudovector (or axial vector) is a quantity that transforms like a vector under a proper rotation
, but gains an additional sign flip under an improper rotation
such as a reflection
. Geometrically it is the opposite, of equal magnitude but in the opposite direction, of its mirror image
. This is as opposed to a true or polar vector (more formally, a contravariant vector), which on reflection matches its mirror image.
In three dimensions the pseudovector p is associated with the cross product
of two polar vectors a and b:
The vector p calculated this way is a pseudovector. One example is the normal to a plane. A plane can be defined by two non-parallel vectors, a and b, which can be said to span the plane. The vector a × b is a normal to the plane (there are two normals, one on each side – which can be determined by the right-hand rule
), and is a pseudovector. This has consequences in computer graphics where it has to be considered when transforming surface normals.
A number of quantities in physics behave as pseudovectors rather than polar vectors, including magnetic field
and angular velocity
. In mathematics pseudovectors are equivalent to three dimensional bivector
s, from which the transformation rules of pseudovectors can be derived. More generally in n-dimensional geometric algebra
pseudovectors are the elements of the algebra with dimension , written Λn−1Rn. The label 'pseudo' can be further generalized to pseudoscalar
s and pseudotensor
s, both of which gain an extra sign flip under improper rotations compared to a true scalar
or tensor
.
, torque
, vorticity, and the angular momentum
.
Often, the distinction between vectors and pseudovectors is overlooked, but it becomes important in understanding and exploiting the effect of symmetry on the solution to physical systems
. For example, consider the case of an electrical current loop in the z = 0 plane, which has a magnetic field at z = 0 that is oriented in the z direction. This system is symmetric (invariant) under mirror reflections through the plane (an improper rotation), so the magnetic field should be unchanged by the reflection. But reflecting the magnetic field through that plane naively appears to change its sign if it is viewed as a vector field—this contradiction is resolved by realizing that the mirror reflection of the field induces an extra sign flip because of its pseudovector nature, so the mirror flip in the end leaves the magnetic field unchanged as expected.
As another example, consider the pseudovector angular momentum
L = r × p. Driving in a car, and looking forward, each of the wheels has an angular momentum vector pointing to the left. If the world is reflected in a mirror which switches the left and right side of the car, the "reflection" of this angular momentum "vector" (viewed as an ordinary vector) points to the right, but the actual angular momentum vector of the wheel still points to the left, corresponding to the extra minus sign in the reflection of a pseudovector. This reflects the fact that the wheels are still turning forward. In comparison, the behaviour of a regular vector, such as the position of the car, is quite different.
To the extent that physical laws would be the same if the universe were reflected in a mirror (equivalently, invariant under parity
), the sum of a vector and a pseudovector is not meaningful. However, the weak force, which governs beta decay
, does depend on the chirality
of the universe, and in this case pseudovectors and vectors are added.
). Under the physics definition, a "vector" is required to have components
that "transform" in a certain way under a proper rotation
: In particular, if everything in the universe were rotated, the vector would rotate in exactly the same way. (The coordinate system is fixed in this discussion; in other words this is the perspective of active transformations
.) Mathematically, if everything in the universe undergoes a rotation described by a rotation matrix R, so that a displacement vector x is transformed to x′ = Rx, then any "vector" v must be similarly transformed to v′ = Rv. This important requirement is what distinguishes a vector (which might be composed of, for example, the x, y, and z-components of velocity
) from any other triplet of physical quantities (For example, the length, width, and height of a rectangular box cannot be considered the three components of a vector, since rotating the box does not appropriately transform these three components.)
(In the language of differential geometry, this requirement is equivalent to defining a vector to be a tensor
of contravariant rank one.)
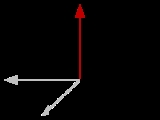
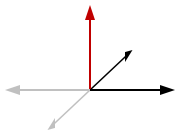
The discussion so far only relates to proper rotations, i.e. rotations about an axis. However, one can also consider improper rotation
s, i.e. a mirror-reflection possibly followed by a proper rotation. (One example of an improper rotation is inversion.) Suppose everything in the universe undergoes an improper rotation described by the rotation matrix R, so that a position vector x is transformed to x′ = Rx. If the vector v is a polar vector, it will be transformed to v′ = Rv. If it is a pseudovector, it will be transformed to v′ = -Rv.
The transformation rules for polar vectors and pseudovectors can be compactly stated as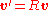
(polar vector)
(pseudovector)
where the symbols are as described above, and the rotation matrix R can be either proper or improper. The symbol det denotes determinant
; this formula works because the determinant of proper and improper rotation matrices are +1 and -1, respectively.
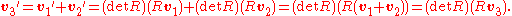
So v3 is also a pseudovector. Similarly one can show that the difference between two pseudovectors is a pseudovector, that the sum or difference of two polar vectors is a polar vector, that multiplying a polar vector by any real number yields another polar vector, and that multiplying a pseudovector by any real number yields another pseudovector.
On the other hand, suppose v1 is known to be a polar vector, v2 is known to be a pseudovector, and v3 is defined to be their sum, v3=v1+v2. If the universe is transformed by a rotation matrix R, then v3 is transformed to
Therefore, v3 is neither a polar vector nor a pseudovector. For an improper rotation, v3 does not in general even keep the same magnitude:
but 
.
If the magnitude of v3 were to describe a measurable physical quantity, that would mean that the laws of physics would not appear the same if the universe was viewed in a mirror. In fact, this is exactly what happens in the weak interaction
: Certain radioactive decays treat "left" and "right" differently, a phenomenon which can be traced to the summation of a polar vector with a pseudovector in the underlying theory. (See parity violation.)
For a rotation matrix R, either proper or improper, the following mathematical equation is always true: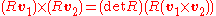
,
where v1 and v2 are any three-dimensional vectors. (This equation can be proven either through a geometric argument or through an algebraic calculation, and is well known.)
Suppose v1 and v2 are known polar vectors, and v3 is defined to be their cross product, v3=v1×v2. If the universe is transformed by a rotation matrix R, then v3 is transformed to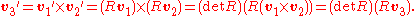
So v3 is a pseudovector. Similarly, one can show:
s. An alternate approach, more along the lines of passive transformation
s, is to keep the universe fixed, but switch "right-hand rule
" with "left-hand rule" and vice-versa everywhere in physics, in particular in the definition of the cross product
. Any polar vector (e.g., a translation vector) would be unchanged, but pseudovectors (e.g., the magnetic field vector at a point) would switch signs. Nevertheless, there would be no physical consequences, apart from in the parity-violating phenomena such as certain radioactive decay
s.
the basic elements are vectors, and these are used to build a hierarchy of elements using the definitions of products in this algebra. In particular, the algebra builds pseudovectors from vectors.
The basic multiplication in the geometric algebra is the geometric product, denoted by simply juxtaposing two vectors as in ab. This product is expressed as:
where the leading term is the customary vector dot product
and the second term is called the wedge product. Using the postulates of the algebra, all combinations of dot and wedge products can be evaluated. A terminology to describe the various combinations is provided. For example, a multivector is a summation of k-fold wedge products of various k-values. A k-fold wedge product also is referred to as a k-blade.
In the present context the pseudovector is one of these combinations. This term is attached to a different mulitvector depending upon the dimension
s of the space (that is, the number of linearly independent vectors in the space). In three dimensions, the most general 2-blade or bivector
can be expressed as a single wedge product and is a pseudovector. In four dimensions, however, the pseudovectors are trivectors
. In general, it is a (n - 1)-blade, where n is the dimension of the space and algebra. An n-dimensional space has n vectors and also n pseudovectors. Each pseudovector is formed from the outer (wedge) product of all but one of the n vectors. For instance, in four dimensions where the vectors are: {e1, e2, e3, e4}, the pseudovectors can be written as: {e234, e134, e124, e123}.
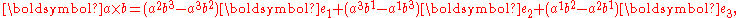
where superscripts label vector components. On the other hand, the plane of the two vectors is represented by the exterior product or wedge product, denoted by . In this context of geometric algebra, this bivector
is called a pseudovector, and is the dual of the cross product. The dual of e1 is introduced as e23 ≡ e2e3 = , and so forth. That is, the dual of e1 is the subspace perpendicular to e1, namely the subspace spanned by e2 and e3. With this understanding,
For details see Hodge dual. Comparison shows that the cross product and wedge product are related by:
where i = is called the unit pseudoscalar. It has the property:
Using the above relations, it is seen that if the vectors a and b are inverted by changing the signs of their components while leaving the basis vectors fixed, both the pseudovector and the cross product are invariant. On the other hand, if the components are fixed and the basis vectors eℓ are inverted, then the pseudovector is invariant, but the cross product changes sign. This behavior of cross products is consistent with their definition as vector-like elements that change sign under transformation from a right-handed to a left-handed coordinate system, unlike polar vectors.
Another important note is that pseudovectors, despite their name, are "vectors" in the common mathematical sense, i.e. elements of a vector space
. The idea that "a pseudovector is different from a vector" is only true with a different and more specific definition of the term "vector" as discussed above.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a pseudovector (or axial vector) is a quantity that transforms like a vector under a proper rotation
Rotation (mathematics)
In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...
, but gains an additional sign flip under an improper rotation
Improper rotation
In 3D geometry, an improper rotation, also called rotoreflection or rotary reflection is, depending on context, a linear transformation or affine transformation which is the combination of a rotation about an axis and a reflection in a plane perpendicular to the axis.Equivalently it is the...
such as a reflection
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
. Geometrically it is the opposite, of equal magnitude but in the opposite direction, of its mirror image
Mirror image
A mirror image is a reflected duplication of an object that appears identical but reversed. As an optical effect it results from reflection off of substances such as a mirror or water. It is also a concept in geometry and can be used as a conceptualization process for 3-D structures...
. This is as opposed to a true or polar vector (more formally, a contravariant vector), which on reflection matches its mirror image.
In three dimensions the pseudovector p is associated with the cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
of two polar vectors a and b:
The vector p calculated this way is a pseudovector. One example is the normal to a plane. A plane can be defined by two non-parallel vectors, a and b, which can be said to span the plane. The vector a × b is a normal to the plane (there are two normals, one on each side – which can be determined by the right-hand rule
Right-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
), and is a pseudovector. This has consequences in computer graphics where it has to be considered when transforming surface normals.
A number of quantities in physics behave as pseudovectors rather than polar vectors, including magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
and angular velocity
Angular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
. In mathematics pseudovectors are equivalent to three dimensional bivector
Bivector
In mathematics, a bivector or 2-vector is a quantity in geometric algebra or exterior algebra that generalises the idea of a vector. If a scalar is considered a zero dimensional quantity, and a vector is a one dimensional quantity, then a bivector can be thought of as two dimensional. Bivectors...
s, from which the transformation rules of pseudovectors can be derived. More generally in n-dimensional geometric algebra
Geometric algebra
Geometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
pseudovectors are the elements of the algebra with dimension , written Λn−1Rn. The label 'pseudo' can be further generalized to pseudoscalar
Pseudoscalar
In physics, a pseudoscalar is a quantity that behaves like a scalar, except that it changes sign under a parity inversion such as improper rotations while a true scalar does not.The prototypical example of a pseudoscalar is the scalar triple product...
s and pseudotensor
Pseudotensor
In physics and mathematics, a pseudotensor is usually a quantity that transforms like a tensor under an orientation preserving coordinate transformation , but gains an additional sign flip under an orientation reversing coordinate transformation In physics and mathematics, a pseudotensor is usually...
s, both of which gain an extra sign flip under improper rotations compared to a true scalar
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
or tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
.
Physical examples
Physical examples of pseudovectors include the magnetic fieldMagnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
, torque
Torque
Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....
, vorticity, and the angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
.
Often, the distinction between vectors and pseudovectors is overlooked, but it becomes important in understanding and exploiting the effect of symmetry on the solution to physical systems
Symmetry in physics
In physics, symmetry includes all features of a physical system that exhibit the property of symmetry—that is, under certain transformations, aspects of these systems are "unchanged", according to a particular observation...
. For example, consider the case of an electrical current loop in the z = 0 plane, which has a magnetic field at z = 0 that is oriented in the z direction. This system is symmetric (invariant) under mirror reflections through the plane (an improper rotation), so the magnetic field should be unchanged by the reflection. But reflecting the magnetic field through that plane naively appears to change its sign if it is viewed as a vector field—this contradiction is resolved by realizing that the mirror reflection of the field induces an extra sign flip because of its pseudovector nature, so the mirror flip in the end leaves the magnetic field unchanged as expected.
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
L = r × p. Driving in a car, and looking forward, each of the wheels has an angular momentum vector pointing to the left. If the world is reflected in a mirror which switches the left and right side of the car, the "reflection" of this angular momentum "vector" (viewed as an ordinary vector) points to the right, but the actual angular momentum vector of the wheel still points to the left, corresponding to the extra minus sign in the reflection of a pseudovector. This reflects the fact that the wheels are still turning forward. In comparison, the behaviour of a regular vector, such as the position of the car, is quite different.
To the extent that physical laws would be the same if the universe were reflected in a mirror (equivalently, invariant under parity
Parity (physics)
In physics, a parity transformation is the flip in the sign of one spatial coordinate. In three dimensions, it is also commonly described by the simultaneous flip in the sign of all three spatial coordinates:...
), the sum of a vector and a pseudovector is not meaningful. However, the weak force, which governs beta decay
Beta decay
In nuclear physics, beta decay is a type of radioactive decay in which a beta particle is emitted from an atom. There are two types of beta decay: beta minus and beta plus. In the case of beta decay that produces an electron emission, it is referred to as beta minus , while in the case of a...
, does depend on the chirality
Chirality (physics)
A chiral phenomenon is one that is not identical to its mirror image . The spin of a particle may be used to define a handedness for that particle. A symmetry transformation between the two is called parity...
of the universe, and in this case pseudovectors and vectors are added.
Details
The definition of a "vector" in physics (including both polar vectors and pseudovectors) is more specific than the mathematical definition of "vector" (namely, any element of an abstract vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
). Under the physics definition, a "vector" is required to have components
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
that "transform" in a certain way under a proper rotation
Rotation (mathematics)
In geometry and linear algebra, a rotation is a transformation in a plane or in space that describes the motion of a rigid body around a fixed point. A rotation is different from a translation, which has no fixed points, and from a reflection, which "flips" the bodies it is transforming...
: In particular, if everything in the universe were rotated, the vector would rotate in exactly the same way. (The coordinate system is fixed in this discussion; in other words this is the perspective of active transformations
Active and passive transformation
In the physical sciences, an active transformation is one which actually changes the physical position of a system, and makes sense even in the absence of a coordinate system whereas a passive transformation is a change in the coordinate description of the physical system . The distinction between...
.) Mathematically, if everything in the universe undergoes a rotation described by a rotation matrix R, so that a displacement vector x is transformed to x′ = Rx, then any "vector" v must be similarly transformed to v′ = Rv. This important requirement is what distinguishes a vector (which might be composed of, for example, the x, y, and z-components of velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
) from any other triplet of physical quantities (For example, the length, width, and height of a rectangular box cannot be considered the three components of a vector, since rotating the box does not appropriately transform these three components.)
(In the language of differential geometry, this requirement is equivalent to defining a vector to be a tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
of contravariant rank one.)
The discussion so far only relates to proper rotations, i.e. rotations about an axis. However, one can also consider improper rotation
Improper rotation
In 3D geometry, an improper rotation, also called rotoreflection or rotary reflection is, depending on context, a linear transformation or affine transformation which is the combination of a rotation about an axis and a reflection in a plane perpendicular to the axis.Equivalently it is the...
s, i.e. a mirror-reflection possibly followed by a proper rotation. (One example of an improper rotation is inversion.) Suppose everything in the universe undergoes an improper rotation described by the rotation matrix R, so that a position vector x is transformed to x′ = Rx. If the vector v is a polar vector, it will be transformed to v′ = Rv. If it is a pseudovector, it will be transformed to v′ = -Rv.
The transformation rules for polar vectors and pseudovectors can be compactly stated as
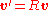(polar vector) (pseudovector)where the symbols are as described above, and the rotation matrix R can be either proper or improper. The symbol det denotes determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
; this formula works because the determinant of proper and improper rotation matrices are +1 and -1, respectively.
Behavior under addition, subtraction, scalar multiplication
Suppose v1 and v2 are known pseudovectors, and v3 is defined to be their sum, v3=v1+v2. If the universe is transformed by a rotation matrix R, then v3 is transformed to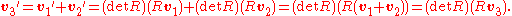So v3 is also a pseudovector. Similarly one can show that the difference between two pseudovectors is a pseudovector, that the sum or difference of two polar vectors is a polar vector, that multiplying a polar vector by any real number yields another polar vector, and that multiplying a pseudovector by any real number yields another pseudovector.
On the other hand, suppose v1 is known to be a polar vector, v2 is known to be a pseudovector, and v3 is defined to be their sum, v3=v1+v2. If the universe is transformed by a rotation matrix R, then v3 is transformed to
Therefore, v3 is neither a polar vector nor a pseudovector. For an improper rotation, v3 does not in general even keep the same magnitude:
but .If the magnitude of v3 were to describe a measurable physical quantity, that would mean that the laws of physics would not appear the same if the universe was viewed in a mirror. In fact, this is exactly what happens in the weak interaction
Weak interaction
Weak interaction , is one of the four fundamental forces of nature, alongside the strong nuclear force, electromagnetism, and gravity. It is responsible for the radioactive decay of subatomic particles and initiates the process known as hydrogen fusion in stars...
: Certain radioactive decays treat "left" and "right" differently, a phenomenon which can be traced to the summation of a polar vector with a pseudovector in the underlying theory. (See parity violation.)
Behavior under cross products
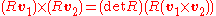,where v1 and v2 are any three-dimensional vectors. (This equation can be proven either through a geometric argument or through an algebraic calculation, and is well known.)
Suppose v1 and v2 are known polar vectors, and v3 is defined to be their cross product, v3=v1×v2. If the universe is transformed by a rotation matrix R, then v3 is transformed to
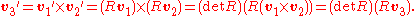
So v3 is a pseudovector. Similarly, one can show:
- polar vector × polar vector = pseudovector
- pseudovector × pseudovector = pseudovector
- polar vector × pseudovector = polar vector
- pseudovector × polar vector = polar vector
Examples
From the definition, it is clear that a displacement vector is a polar vector. The velocity vector is a displacement vector (a polar vector) divided by time (a scalar), so is also a polar vector. Likewise, the momentum vector is the velocity vector (a polar vector) times mass (a scalar), so is a polar vector. Angular momentum is the cross product of a displacement (a polar vector) and momentum (a polar vector), and is therefore a pseudovector. Continuing this way, it is straightforward to classify any vector as either a pseudovector or polar vector.The right-hand rule
Above, pseudovectors have been discussed using active transformationActive and passive transformation
In the physical sciences, an active transformation is one which actually changes the physical position of a system, and makes sense even in the absence of a coordinate system whereas a passive transformation is a change in the coordinate description of the physical system . The distinction between...
s. An alternate approach, more along the lines of passive transformation
Active and passive transformation
In the physical sciences, an active transformation is one which actually changes the physical position of a system, and makes sense even in the absence of a coordinate system whereas a passive transformation is a change in the coordinate description of the physical system . The distinction between...
s, is to keep the universe fixed, but switch "right-hand rule
Right-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
" with "left-hand rule" and vice-versa everywhere in physics, in particular in the definition of the cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
. Any polar vector (e.g., a translation vector) would be unchanged, but pseudovectors (e.g., the magnetic field vector at a point) would switch signs. Nevertheless, there would be no physical consequences, apart from in the parity-violating phenomena such as certain radioactive decay
Radioactive decay
Radioactive decay is the process by which an atomic nucleus of an unstable atom loses energy by emitting ionizing particles . The emission is spontaneous, in that the atom decays without any physical interaction with another particle from outside the atom...
s.
Geometric algebra
In geometric algebraGeometric algebra
Geometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
the basic elements are vectors, and these are used to build a hierarchy of elements using the definitions of products in this algebra. In particular, the algebra builds pseudovectors from vectors.
The basic multiplication in the geometric algebra is the geometric product, denoted by simply juxtaposing two vectors as in ab. This product is expressed as:
where the leading term is the customary vector dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
and the second term is called the wedge product. Using the postulates of the algebra, all combinations of dot and wedge products can be evaluated. A terminology to describe the various combinations is provided. For example, a multivector is a summation of k-fold wedge products of various k-values. A k-fold wedge product also is referred to as a k-blade.
In the present context the pseudovector is one of these combinations. This term is attached to a different mulitvector depending upon the dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s of the space (that is, the number of linearly independent vectors in the space). In three dimensions, the most general 2-blade or bivector
Bivector
In mathematics, a bivector or 2-vector is a quantity in geometric algebra or exterior algebra that generalises the idea of a vector. If a scalar is considered a zero dimensional quantity, and a vector is a one dimensional quantity, then a bivector can be thought of as two dimensional. Bivectors...
can be expressed as a single wedge product and is a pseudovector. In four dimensions, however, the pseudovectors are trivectors
Multivector
In multilinear algebra, a multivector or clif is an element of the exterior algebra on a vector space, \Lambda^* V. This algebra consists of linear combinations of simple k-vectors v_1\wedge\cdots\wedge v_k."Multivector" may mean either homogeneous elements In multilinear algebra, a multivector...
. In general, it is a (n - 1)-blade, where n is the dimension of the space and algebra. An n-dimensional space has n vectors and also n pseudovectors. Each pseudovector is formed from the outer (wedge) product of all but one of the n vectors. For instance, in four dimensions where the vectors are: {e1, e2, e3, e4}, the pseudovectors can be written as: {e234, e134, e124, e123}.
Transformations in three dimensions
The transformation properties of the pseudovector in three dimensions has been compared to that of the vector cross product by Baylis. He says: "The terms axial vector and pseudovector are often treated as synonymous, but it is quite useful to be able to distinguish a bivector ⋯ from its dual ⋯." To paraphrase Baylis: Given two polar vectors (that is, true vectors) a and b in three dimensions, the cross product composed from a and b is the vector normal to their plane given by c = . Given a set of right-handed orthonormal basis vectors }, the cross product is expressed in terms of its components as: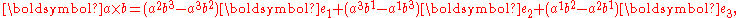where superscripts label vector components. On the other hand, the plane of the two vectors is represented by the exterior product or wedge product, denoted by . In this context of geometric algebra, this bivector
Bivector
In mathematics, a bivector or 2-vector is a quantity in geometric algebra or exterior algebra that generalises the idea of a vector. If a scalar is considered a zero dimensional quantity, and a vector is a one dimensional quantity, then a bivector can be thought of as two dimensional. Bivectors...
is called a pseudovector, and is the dual of the cross product. The dual of e1 is introduced as e23 ≡ e2e3 = , and so forth. That is, the dual of e1 is the subspace perpendicular to e1, namely the subspace spanned by e2 and e3. With this understanding,
For details see Hodge dual. Comparison shows that the cross product and wedge product are related by:
where i = is called the unit pseudoscalar. It has the property:
Using the above relations, it is seen that if the vectors a and b are inverted by changing the signs of their components while leaving the basis vectors fixed, both the pseudovector and the cross product are invariant. On the other hand, if the components are fixed and the basis vectors eℓ are inverted, then the pseudovector is invariant, but the cross product changes sign. This behavior of cross products is consistent with their definition as vector-like elements that change sign under transformation from a right-handed to a left-handed coordinate system, unlike polar vectors.
Note on usage
As an aside, it may be noted that not all authors in the field of geometric algebra use the term pseudovector, and some authors follow the terminology that does not distinguish between the pseudovector and the cross product. However, because the cross product does not generalize beyond three dimensions, the notion of pseudovector based upon the cross product also cannot be extended to higher dimensions. The pseudovector as the (n–1)-blade of an n-dimensional space is not so restricted.Another important note is that pseudovectors, despite their name, are "vectors" in the common mathematical sense, i.e. elements of a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
. The idea that "a pseudovector is different from a vector" is only true with a different and more specific definition of the term "vector" as discussed above.
See also
- Grassmann algebra
- Clifford algebraClifford algebraIn mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
- Orientation (mathematics)Orientation (mathematics)In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
- Description of oriented spaces, necessary for pseudovectors - OrientabilityOrientabilityIn mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
- Discussion about non-orientable spaces.