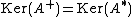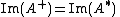Pseudoinverse
Encyclopedia
In mathematics
, and in particular linear algebra
, a pseudoinverse of a matrix
is a generalization
of the inverse matrix. The most widely known type of matrix pseudoinverse is the Moore–Penrose pseudoinverse, which was independently described by E. H. Moore
in 1920, Arne Bjerhammar
in 1951 and Roger Penrose
in 1955. Earlier, Fredholm
had introduced the concept of a pseudoinverse of integral operators in 1903. When referred to a matrix, the term pseudoinverse, without further specification, is often used to indicate the Moore–Penrose pseudoinverse. The term generalized inverse
is sometimes used as a synonym for pseudoinverse.
A common use of the Moore–Penrose pseudoinverse (hereafter, just pseudoinverse) is to compute a 'best fit' (least squares
) solution to a system of linear equations that lacks a unique solution (see below under Applications).
Another use is to find the minimum (Euclidean
) norm solution to a system of linear equations with multiple solutions.
The pseudoinverse is defined and unique for all matrices whose entries are real
or complex
numbers. It can be computed using the singular value decomposition
.
,
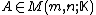a Moore–Penrose pseudoinverse (hereafter, just pseudoinverse) of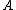
is defined as a matrix
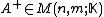
satisfying all of the following four criteria:
A matrix satisfying the first two conditions of the definition is known as a generalized inverse
. Generalized inverses always exist but are not in general unique. Uniqueness is a consequence of the last two conditions.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and in particular linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a pseudoinverse of a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
is a generalization
Generalized inverse
In mathematics, a generalized inverse or pseudoinverse of a matrix A is a matrix that has some properties of the inverse matrix of A but not necessarily all of them...
of the inverse matrix. The most widely known type of matrix pseudoinverse is the Moore–Penrose pseudoinverse, which was independently described by E. H. Moore
E. H. Moore
Eliakim Hastings Moore was an American mathematician.-Life:Moore, the son of a Methodist minister and grandson of US Congressman Eliakim H. Moore, discovered mathematics through a summer job at the Cincinnati Observatory while in high school. He learned mathematics at Yale University, where he was...
in 1920, Arne Bjerhammar
Arne Bjerhammar
Arne Bjerhammar was a Swedish geodesist. He was professor at Royal Institute of Technology in Stockholm. He was born in Båstad, Scania in the south of Sweden.His research covered many fields of geodesy...
in 1951 and Roger Penrose
Roger Penrose
Sir Roger Penrose OM FRS is an English mathematical physicist and Emeritus Rouse Ball Professor of Mathematics at the Mathematical Institute, University of Oxford and Emeritus Fellow of Wadham College...
in 1955. Earlier, Fredholm
Erik Ivar Fredholm
Erik Ivar Fredholm was a Swedish mathematician who established the modern theory of integral equations. His 1903 paper in Acta Mathematica is considered to be one of the major landmarks in the establishment of operator theory.The lunar crater Fredholm is named after him.-List of publications:* E.I...
had introduced the concept of a pseudoinverse of integral operators in 1903. When referred to a matrix, the term pseudoinverse, without further specification, is often used to indicate the Moore–Penrose pseudoinverse. The term generalized inverse
Generalized inverse
In mathematics, a generalized inverse or pseudoinverse of a matrix A is a matrix that has some properties of the inverse matrix of A but not necessarily all of them...
is sometimes used as a synonym for pseudoinverse.
A common use of the Moore–Penrose pseudoinverse (hereafter, just pseudoinverse) is to compute a 'best fit' (least squares
Linear least squares
In statistics and mathematics, linear least squares is an approach to fitting a mathematical or statistical model to data in cases where the idealized value provided by the model for any data point is expressed linearly in terms of the unknown parameters of the model...
) solution to a system of linear equations that lacks a unique solution (see below under Applications).
Another use is to find the minimum (Euclidean
Euclidean
Euclidean relates to Euclid , a town or others. It may refer to:Geometry...
) norm solution to a system of linear equations with multiple solutions.
The pseudoinverse is defined and unique for all matrices whose entries are real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
numbers. It can be computed using the singular value decomposition
Singular value decomposition
In linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
.
Notation
In the following discussion, the following conventions are adopted.
will denote one of the fields of real or complex numbers, denoted 
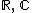, respectively. The ring of 
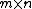matrices over 
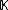is denoted by 
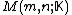.- For
, 
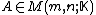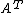and 
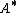denote the transpose and Hermitian transpose (also called conjugate transposeConjugate transposeIn mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
) respectively. If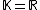
, then 
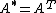. - For
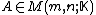, then 
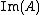denotes the rangeRange (mathematics)In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
(image) of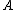
(the space spanned by the column vectors of 
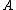) and 
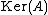denotes the kernel (null space) of 
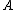. - Finally, for any positive integer
, 
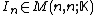denotes the 
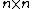identity matrixIdentity matrixIn linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
.
Definition
For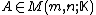,a Moore–Penrose pseudoinverse (hereafter, just pseudoinverse) of
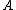is defined as a matrix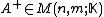satisfying all of the following four criteria:
-
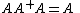( need not be the general identity matrix, but it maps all column vectors of to themselves); -
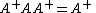( is a weak inverse for the multiplicative semigroupSemigroupIn mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
); -
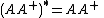( is Hermitian); and -
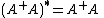( is also Hermitian).
Properties
Proofs for some of these facts may be found on a separate page here.Existence and uniqueness
- The Moore–Penrose pseudoinverse exists and is unique: for any matrix
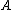, there is precisely one matrix 
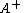, that satisfies the four properties of the definition.
A matrix satisfying the first two conditions of the definition is known as a generalized inverse
Generalized inverse
In mathematics, a generalized inverse or pseudoinverse of a matrix A is a matrix that has some properties of the inverse matrix of A but not necessarily all of them...
. Generalized inverses always exist but are not in general unique. Uniqueness is a consequence of the last two conditions.
Basic properties
- If
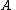has real entries, then so does 
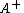. - If
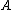is invertible, the pseudoinverse and the inverse coincide: 
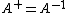. - The pseudoinverse of a zero matrix is its transpose.
- The pseudoinverse of the pseudoinverse is the original matrix:
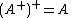. - Pseudoinversion commutes with transposition, conjugation, and taking the conjugate transpose:
-
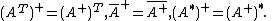
- The pseudoinverse of a scalar multiple of is the reciprocal multiple of :
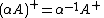for 
.
Identities
The following identities can be used to cancel certain subexpressions or expand expressions involving pseudoinverses. Proofs for these properties can be found in the proofs subpage.-
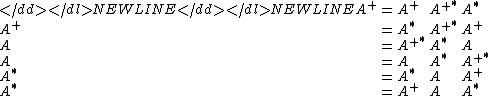
Reduction to Hermitian case
.
.
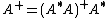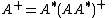Products
If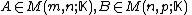
and either,
-
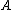has orthonormal columns (i.e. 
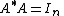) or, -
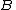has orthonormal rows (i.e. 
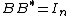) or, -
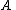has all columns linearly independent (full column rank) and 
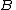has all rows linearly independent (full row rank),
then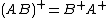
.
Projectors
If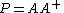
and 
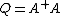are
orthogonal projection operatorsProjection (linear algebra)In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself such that P2 = P. It leaves its image unchanged....
i.e.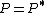
, 
, 
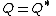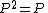and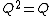 
i.e. they are Hermitian and idempotent.
Then the following hol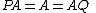d:
and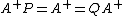 
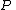is the orthogonal projector onto the rangeRange (mathematics)In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
of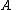
(which equals the orthogonal complement of the kernel of 
).
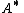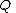is the orthogonal projector onto the rangeRange (mathematics)In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
of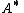
(which equals the orthogonal complement of the kernel of 
).
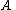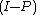is the orthogonal projector onto the kernel of 
.
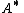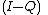is the orthogonal projector onto the kernel of 
.
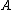Subspaces
Limit relations
- The pseudoinverse can also be computed via limiting processes:
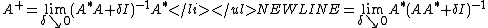. These limits exist even if 
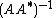or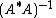 
do not exist.
Continuity
- In contrast to ordinary matrix inversion, the process of taking pseudoinverses is not continuousContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
: if the sequence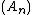
converges to the matrix (in the maximum norm or Frobenius norm, say), then need not converge to . However, if all the matrices have the same rank, will converge to .
Scalars
It is also possible to define a pseudoinverse for scalars and vectors. This amounts to treating these as matrices. The pseudoinverse of a scalar is zero if is zero and the reciprocal of otherwise: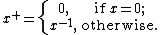
Vectors
The pseudoinverse of the null (all zero) vector is the transposed null vector. The pseudoinverse of a non-null vector is the conjugate transposed vector divided by its squared magnitude: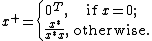
Linearly independent columns
If the columns of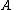
are linearly independentLinear independenceIn linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
(so that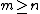
), then
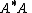is invertible. In this case, an explicit formula is:
.
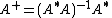It follows that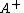
is then a left inverse of
: 
.
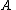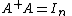Linearly independent rows
If the rows of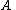
are linearly independent (so that 
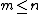), then
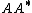is invertible. In this case, an explicit formula is:
.
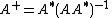It follows that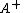
is a right inverse of
: 
.
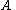Orthonormal columns or rows
This is a special case of either full column rank or full row rank (treated above).
If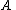
has orthonormal columns (
)
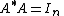or orthonormal rows (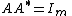
),
then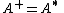
.
Circulant matrices
For a Circulant matrixCirculant matrixIn linear algebra, a circulant matrix is a special kind of Toeplitz matrix where each row vector is rotated one element to the right relative to the preceding row vector. In numerical analysis, circulant matrices are important because they are diagonalized by a discrete Fourier transform, and hence...
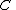, the singular value decomposition is given by the Fourier transformFourier transformIn mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
,
that is the singular values are the Fourier coefficients.
Let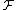
be the Discrete Fourier Transform (DFT) matrixDFT matrixA DFT matrix is an expression of a discrete Fourier transform as a matrix multiplication.-Definition:An N-point DFT is expressed as an N-by-N matrix multiplication as X = W x, where x is the original input signal, and X is the DFT of the signal.The transformation W of size N\times N can be defined...
, then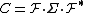
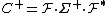
Rank decomposition
Let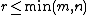
denote the rank of
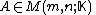. Then 
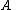can be (rank) decomposedRank factorizationGiven an m \times n matrix A of rank r, a rank decomposition or rank factorization of A is a product A=CF, where C is an m \times r matrix and F is an r \times n matrix....
as
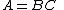where
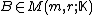and
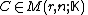are of rank 
.
Then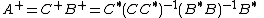
.
The QR method
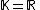For
or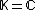 
computing the product
or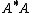 
and their inverses explicitly is often a source of numerical rounding errors and computational cost in practice.
An alternative approach using the QR decompositionQR decompositionIn linear algebra, a QR decomposition of a matrix is a decomposition of a matrix A into a product A=QR of an orthogonal matrix Q and an upper triangular matrix R...
of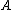
may be used instead.
Considering the case when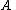
is of full column rank, so that
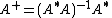. then the Cholesky decompositionCholesky decompositionIn linear algebra, the Cholesky decomposition or Cholesky triangle is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose. It was discovered by André-Louis Cholesky for real matrices...
,
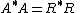where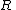
is an upper triangular matrix, may be used.
Multiplication by the inverse is then done easily by solving a system with multiple right-hand-sides,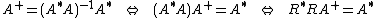
which may be solved by forward substitution followed by back substitution.
The Cholesky decomposition may be computed without forming
explicitly, by alternatively using the QR decompositionQR decompositionIn linear algebra, a QR decomposition of a matrix is a decomposition of a matrix A into a product A=QR of an orthogonal matrix Q and an upper triangular matrix R...
of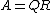
,
where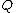
has orthonormal columns, 
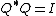, and
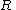is upper triangular. Then
,
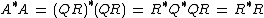so is the Cholesky factor of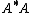
.
The case of full row rank is treated similarly by using the formula
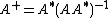and using a similar argument, swapping the roles of 
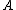and
.
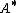Singular value decomposition (SVD)
A computationally simple and accurate way to compute the pseudoinverse is by using the singular value decompositionSingular value decompositionIn linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
. If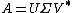
is the singular value decomposition of , then 
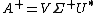. For a diagonal matrixDiagonal matrixIn linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
such as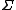
, we get the pseudoinverse by taking the reciprocal of each non-zero element on the diagonal, leaving the zeros in place, and transposing the resulting matrix. In numerical computation, only elements larger than some small tolerance are taken to be nonzero, and the others are replaced by zeros. For example, in the MATLABMATLABMATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
or NumPy function pinv, the tolerance is taken to be , where ε is the machine epsilonMachine epsilonMachine epsilon gives an upper bound on the relative error due to rounding in floating point arithmetic. This value characterizes computer arithmetic in the field of numerical analysis, and by extension in the subject of computational science...
.
The computational cost of this method is dominated by the cost of computing the SVD, which is several times higher than matrix-matrix multiplication, even if a state-of-the art implementation (such as that of LAPACKLAPACK-External links:* : a modern replacement for PLAPACK and ScaLAPACK* on Netlib.org* * * : a modern replacement for LAPACK that is MultiGPU ready* on Sourceforge.net* * optimized LAPACK for Solaris OS on SPARC/x86/x64 and Linux* * *...
) is used.
The above procedure shows why taking the pseudoinverse is not a continuous operation: if the original matrix has a singular value 0 (a diagonal entry of the matrix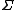
above), then modifying slightly may turn this zero into a tiny positive number, thereby affecting the pseudoinverse dramatically as we now have to take the reciprocal of a tiny number.
Block matrices
Optimized approachesBlock matrix pseudoinverseIn mathematics, block matrix pseudoinverse is a formula of pseudoinverse of a partitioned matrix. This is useful for decomposing or approximating many algorithms updating parameters in signal processing, which are based on least squares method.- Derivation :...
exist for calculating the pseudoinverse of block structured matrices.
The iterative method of Ben-Israel and Cohen
Another method for computing the pseudoinverse uses the recursion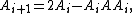
which is sometimes referred to as hyper-power sequence. This recursion produces a sequence converging quadratically to the pseudoinverse of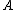
if it is started with an appropriate 
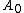satisfying 
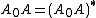. The choice 
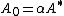(where 
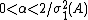, with 
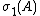denoting the largest singular value of 
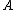) has been argued not to be competitive to the method using the SVD mentioned above, because even for moderately ill-conditioned matrices it takes a long time before 
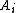enters the region of quadratic convergence. However, if started with 
already close to the Moore–Penrose pseudoinverse and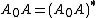 
, for example 
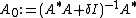, convergence is fast (quadratic).
Updating the pseudoinverse
For the cases where has full row or column rank, and the inverse of the correlation matrix (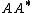
for with full row rank or 
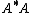for full column rank) is already known, the pseudoinverse for matrices related to 
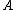can be computed by applying the Sherman–Morrison–Woodbury formula to update the inverse of the correlation matrix, which may need less work. In particular, if the related matrix differs from the original one by only a changed, added or deleted row or column, incremental algorithms exist that exploit the relationship.
Similarly, it is possible to update the Cholesky factor when a row or column is added, without creating the inverse of the correlation matrix explicitly. However, updating the pseudoinverse in the general rank-deficient case is much more complicated.
Software libraries
The package NumPy provides a pseudo-inverse calculation through its functions matrix.I and linalg.pinv. High quality implementations of SVD, QR, and back substitution are available in standard libraries, such as LAPACKLAPACK-External links:* : a modern replacement for PLAPACK and ScaLAPACK* on Netlib.org* * * : a modern replacement for LAPACK that is MultiGPU ready* on Sourceforge.net* * optimized LAPACK for Solaris OS on SPARC/x86/x64 and Linux* * *...
. Writing one's own implementation of SVD is a major programming project that requires a significant numerical expertise. In special circumstances, such as parallel computingParallel computingParallel computing is a form of computation in which many calculations are carried out simultaneously, operating on the principle that large problems can often be divided into smaller ones, which are then solved concurrently . There are several different forms of parallel computing: bit-level,...
or embedded computing, however, alternative implementations by QR or even the use of an explicit inverse might be preferable, and custom implementations may be unavoidable.
Linear least-squares
The pseudoinverse provides a least squaresLinear least squaresIn statistics and mathematics, linear least squares is an approach to fitting a mathematical or statistical model to data in cases where the idealized value provided by the model for any data point is expressed linearly in terms of the unknown parameters of the model...
solution to a system of linear equations.
For
, given a system of linear equations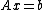
,
in general, a vector
which solves the system may not exist, or if one exists, it may not be unique. The pseudoinverse solves the "least-squares" problem as follows:
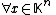, we have 
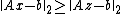where 
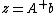and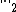 
denotes the Euclidean norm. This weak inequality holds with equality if and only if 
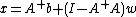for any vector w; this provides an infinitude of minimizing solutions unless A has full column rank, in which case 
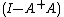is a zero matrix.
This result is easily extended to systems with multiple right-hand sides, when the Euclidean norm is replaced by
the Frobenius norm. Let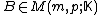
.
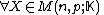, we have 
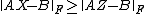where 
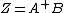and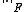 
denotes the Frobenius norm.
Obtaining all solutions of a linear system
If the linear system
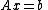
has any solutions, they are all given by
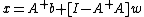
for arbitrary vector w. Solution(s) exist if and only if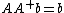
. If the latter holds, then the solution is unique if and only if A has full column rank, in which case 
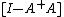is a zero matrix.
Minimum-norm solution to a linear system
For linear systems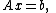
with non-unique solutions (such as under-determined systems), the pseudoinverse may be used to construct the solution of minimum Euclidean norm
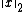among all solutions.
- If
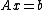is satisfiable, the vector 
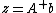is a solution, and satisfies 
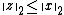for all solutions.
This result is easily extended to systems with multiple right-hand sides, when the Euclidean norm is replaced by
the Frobenius norm. Let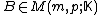
.
- If
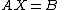is satisfiable, the matrix 
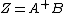is a solution, and satisfies 
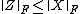for all solutions.
Geometric construction
This description suggests the following geometric construction for the result of applying the pseudoinverse of an × matrix to a vector. To find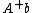
for given in , first project orthogonally onto the range of , finding a point in the range. Then form , i.e. find those vectors in that sends to . This will be an affine subspace of parallel to the kernel of . The element of this subspace that has the smallest length (i.e. is closest to the origin) is the answer 
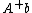we are looking for. It can be found by taking an arbitrary member of and projecting it orthogonally onto the orthogonal complement of the kernel of .
Condition number
Using the pseudoinverse and a matrix norm, one can define a condition numberCondition numberIn the field of numerical analysis, the condition number of a function with respect to an argument measures the asymptotically worst case of how much the function can change in proportion to small changes in the argument...
for any matrix: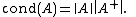
A large condition number implies that the problem of finding least-squares solutions to the corresponding system of linear equations is ill-conditioned in the sense that small errors in the entries of can lead to huge errors in the entries of the solution.
Generalizations
In order to solve more general least-squares problems, one could try to define Moore–Penrose pseudoinverses for all continuous linear operators between two Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s and , using the same four conditions as in our definition above. It turns out that not every continuous linear operator has a continuous linear pseudo-inverse in this sense. Those that do are precisely the ones whose range is closedClosed setIn geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
in .
In abstract algebraAbstract algebraAbstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a Moore–Penrose pseudoinverse may be defined on a *-regular semigroup. This abstract definition coincides with the one in linear algebra.
See also
- Proofs involving the Moore–Penrose pseudoinverse
- Drazin inverseDrazin inverseIn mathematics, the Drazin inverse, named after Michael P. Drazin, is a kind of generalized inverse of a matrix.Let A be a square matrix. The index of A is the least nonnegative integer k such that rank = rank...
- Hat matrixHat matrixIn statistics, the hat matrix, H, maps the vector of observed values to the vector of fitted values. It describes the influence each observed value has on each fitted value...
- Inverse elementInverse elementIn abstract algebra, the idea of an inverse element generalises the concept of a negation, in relation to addition, and a reciprocal, in relation to multiplication. The intuition is of an element that can 'undo' the effect of combination with another given element...
- Linear least squaresLinear least squaresIn statistics and mathematics, linear least squares is an approach to fitting a mathematical or statistical model to data in cases where the idealized value provided by the model for any data point is expressed linearly in terms of the unknown parameters of the model...
- Pseudo-determinantPseudo-determinantIn linear algebra and statistics, the pseudo-determinant is the product of all non-zero eigenvalues of a square matrix. It coincides with the regular determinant when the matrix is non-singular.- Definition :...
- Von Neumann regular ringVon Neumann regular ringIn mathematics, a von Neumann regular ring is a ring R such that for every a in R there exists an x in R withOne may think of x as a "weak inverse" of a...
External links
- In contrast to ordinary matrix inversion, the process of taking pseudoinverses is not continuous
