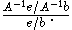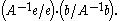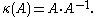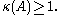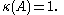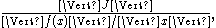Condition number
Encyclopedia
In the field of numerical analysis
, the condition number of a function with respect to an argument measures the asymptotically worst case of how much the function can change in proportion to small changes in the argument. The "function" is the solution of a problem and the "arguments" are the data in the problem.
A problem with a low condition number is said to be well-conditioned, while a problem with a high condition number is said to be ill-conditioned.
The condition number is a property of the problem. Paired with the problem are any number of algorithms that can be used to solve the problem, that is, to calculate the solution. Some algorithms have a property called backward stability
. In general, a backward stable algorithm can be expected to accurately solve well-conditioned problems. Numerical analysis textbooks give formulas for the condition numbers of problems and identify the backward stable algorithms.
As a general rule of thumb, if the condition number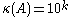
, then you may lose up to 
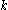digits of accuracy on top of what would be lost to the numerical method due to loss of precision from arithmetic methods. However, the condition number does not give the exact value of the maximum inaccuracy that may occur in the algorithm. It generally just bounds it with an estimate (whose computed value depends on the choice of the norm to measure the inaccuracy).
Ax = b gives a bound on how inaccurate the solution x will be after approximate solution. Note that this is before the effects of round-off error
are taken into account; conditioning is a property of the matrix, not the algorithm
or floating point
accuracy of the computer used to solve the corresponding system. In particular, one should think of the condition number as being (very roughly) the rate at which the solution, x, will change with respect to a change in b. Thus, if the condition number is large, even a small error in b may cause a large error in x. On the other hand, if the condition number is small then the error in x will not be much bigger than the error in b.
The condition number is defined more precisely to be the maximum ratio of the relative error in x divided by the relative error in b.
Let e be the error in b. Assuming that A is a square matrix, the error in the solution A−1b is A−1e. The ratio of the relative error in the solution to the relative error in b is
This is easily transformed to
The maximum value (for nonzero b and e) is easily seen to be the product of the two operator norm
s:
The same definition is used for any consistent norm, i.e. one that satisfies
When the condition number is exactly one, then the algorithm may find an approximation of the solution with an arbitrary precision. However it does not mean that the algorithm will converge rapidly to this solution, just that it won't diverge arbitrarily because of inaccuracy on the source data (backward error), provided that the forward error introduced by the algorithm does not diverge as well because of accumulating intermediate rounding errors.
The condition number may also be infinite, in which case the algorithm will not reliably find a solution to the problem, not even a weak approximation of it (and not even its order of magnitude) with any reasonable and provable accuracy.
Of course, this definition depends on the choice of norm:
[e.g. an n-tuple of real numbers ƒ(x)], where both the domain and codomain are Banach space
s. They express how sensitive that function is to small changes (or small errors) in its arguments. This is crucial in assessing the sensitivity and potential accuracy difficulties of numerous computational problems, for example polynomial
root finding or computing eigenvalues.
The condition number of ƒ at a point x (specifically, its relative condition number) is then defined to be the maximum ratio of the fractional change in ƒ(x) to any fractional change in x, in the limit where the change δx in x becomes infinitesimally small:
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, the condition number of a function with respect to an argument measures the asymptotically worst case of how much the function can change in proportion to small changes in the argument. The "function" is the solution of a problem and the "arguments" are the data in the problem.
A problem with a low condition number is said to be well-conditioned, while a problem with a high condition number is said to be ill-conditioned.
The condition number is a property of the problem. Paired with the problem are any number of algorithms that can be used to solve the problem, that is, to calculate the solution. Some algorithms have a property called backward stability
Numerical stability
In the mathematical subfield of numerical analysis, numerical stability is a desirable property of numerical algorithms. The precise definition of stability depends on the context, but it is related to the accuracy of the algorithm....
. In general, a backward stable algorithm can be expected to accurately solve well-conditioned problems. Numerical analysis textbooks give formulas for the condition numbers of problems and identify the backward stable algorithms.
As a general rule of thumb, if the condition number
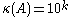, then you may lose up to 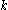digits of accuracy on top of what would be lost to the numerical method due to loss of precision from arithmetic methods. However, the condition number does not give the exact value of the maximum inaccuracy that may occur in the algorithm. It generally just bounds it with an estimate (whose computed value depends on the choice of the norm to measure the inaccuracy).Matrices
For example, the condition number associated with the linear equationLinear equation
A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable....
Ax = b gives a bound on how inaccurate the solution x will be after approximate solution. Note that this is before the effects of round-off error
Round-off error
A round-off error, also called rounding error, is the difference between the calculated approximation of a number and its exact mathematical value. Numerical analysis specifically tries to estimate this error when using approximation equations and/or algorithms, especially when using finitely many...
are taken into account; conditioning is a property of the matrix, not the algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
or floating point
Floating point
In computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
accuracy of the computer used to solve the corresponding system. In particular, one should think of the condition number as being (very roughly) the rate at which the solution, x, will change with respect to a change in b. Thus, if the condition number is large, even a small error in b may cause a large error in x. On the other hand, if the condition number is small then the error in x will not be much bigger than the error in b.
The condition number is defined more precisely to be the maximum ratio of the relative error in x divided by the relative error in b.
Let e be the error in b. Assuming that A is a square matrix, the error in the solution A−1b is A−1e. The ratio of the relative error in the solution to the relative error in b is
This is easily transformed to
The maximum value (for nonzero b and e) is easily seen to be the product of the two operator norm
Operator norm
In mathematics, the operator norm is a means to measure the "size" of certain linear operators. Formally, it is a norm defined on the space of bounded linear operators between two given normed vector spaces.- Introduction and definition :...
s:
The same definition is used for any consistent norm, i.e. one that satisfies
When the condition number is exactly one, then the algorithm may find an approximation of the solution with an arbitrary precision. However it does not mean that the algorithm will converge rapidly to this solution, just that it won't diverge arbitrarily because of inaccuracy on the source data (backward error), provided that the forward error introduced by the algorithm does not diverge as well because of accumulating intermediate rounding errors.
The condition number may also be infinite, in which case the algorithm will not reliably find a solution to the problem, not even a weak approximation of it (and not even its order of magnitude) with any reasonable and provable accuracy.
Of course, this definition depends on the choice of norm:
- If
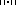is the norm (usually noted as 
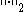) defined in the square-summable sequence spaceSequence spaceIn functional analysis and related areas of mathematics, a sequence space is a vector space whose elements are infinite sequences of real or complex numbers. Equivalently, it is a function space whose elements are functions from the natural numbers to the field K of real or complex numbers...
ℓ2Lp spaceIn mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
(which also matches the usual distance in a continuous and isotropic cartesian space), then-
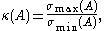
- where
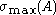and 
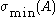are maximal and minimal singular values of 
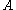respectively. - Hence
- If
is normalNormal matrixA complex square matrix A is a normal matrix ifA^*A=AA^* \ where A* is the conjugate transpose of A. That is, a matrix is normal if it commutes with its conjugate transpose.If A is a real matrix, then A*=AT...
then-
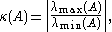
- where
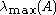and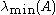 
are maximal and minimal (by moduli) eigenvalues of 
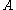respectively.
-
- If
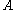is unitary then
-
- If
- This number arises so often in numerical linear algebraLinear algebraLinear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
that it is given a name, the condition number of a matrix.
-
- If
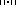is the norm (usually noted as 
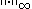) defined in the sequence spaceSequence spaceIn functional analysis and related areas of mathematics, a sequence space is a vector space whose elements are infinite sequences of real or complex numbers. Equivalently, it is a function space whose elements are functions from the natural numbers to the field K of real or complex numbers...
ℓ∞Lp spaceIn mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
of all boundedBounded operatorIn functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
sequences (which also matches the non-linear distance measured as the maximum of distances measured on projections into the base subspaces, without requiring the space to be isotropic or even just linear, but only continuous, such norm being definable on all Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s), and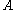
is lower triangularTriangular matrixIn the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
non-singular (i.e.,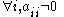
) then
-
- The condition number computed with this norm is generally larger than the condition number computed with square-summable sequences, but it can be evaluated more easily (and this is often the only measurable condition number, when the problem to solve involves a non-linear algebra, for example when approximating irrational and transcendental functions or numbers with numerical methods.)
-
Other contexts
Condition numbers can be defined for any function ƒ mapping its data from some domain (e.g. an m-tuple of real numbers x) into some codomainCodomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
[e.g. an n-tuple of real numbers ƒ(x)], where both the domain and codomain are Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s. They express how sensitive that function is to small changes (or small errors) in its arguments. This is crucial in assessing the sensitivity and potential accuracy difficulties of numerous computational problems, for example polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
root finding or computing eigenvalues.
The condition number of ƒ at a point x (specifically, its relative condition number) is then defined to be the maximum ratio of the fractional change in ƒ(x) to any fractional change in x, in the limit where the change δx in x becomes infinitesimally small:
-
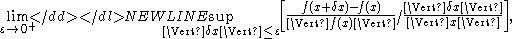
where
is a normNorm (mathematics)In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
on the domain/codomain of ƒ(x).
If ƒ is differentiable, this is equivalent to:
where J denotes the Jacobian matrix of partial derivativePartial derivativeIn mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s of ƒ and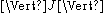
is the induced norm on the matrix.
External links
- Condition Number of a Matrix at Holistic Numerical Methods Institute
-
