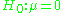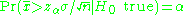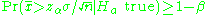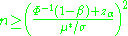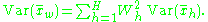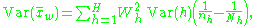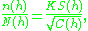Sample size
Encyclopedia
Sample size determination is the act of choosing the number of observations to include in a statistical sample. The sample size is an important feature of any empirical study in which the goal is to make inferences
about a population
from a sample. In practice, the sample size used in a study is determined based on the expense of data collection, and the need to have sufficient statistical power
. In complicated studies there may be several different sample sizes involved in the study: for example, in as survey sampling
involving stratified sampling
there would be different sample sizes for each population. In a census
, data are collected on the entire population, hence the sample size is equal to the population size. In experimental design, where a study may be divided into different treatment groups, there may be different sample sizes for each group.
Sample sizes may be chosen in several different ways:
How samples are collected is discussed in sampling (statistics)
and survey data collection
.
when estimating unknown parameters. For example, if we wish to know the proportion of a certain species of fish that is infected with a pathogen, we would generally have a more accurate estimate of this proportion if we sampled and examined 200, rather than 100 fish. Several fundamental facts of mathematical statistics describe this phenomenon, including the law of large numbers
and the central limit theorem
.
In some situations, the increase in accuracy for larger sample sizes is minimal, or even non-existent. This can result from the presence of systematic error
s or strong dependence in the data, or if the data follow a heavy-tailed distribution.
Sample sizes are judged based on the quality of the resulting estimates. For example, if a proportion is being estimated, one may wish to have the 95% confidence interval
be less than 0.06 units wide. Alternatively, sample size may be assessed based on the power
of a hypothesis test. For example, if we are comparing the support for a certain political candidate among women with the support for that candidate among men, we may wish to have 80% power to detect a difference in the support levels of 0.04 units.
. For example, we may wish to estimate the proportion of residents in a community who are at least 65 years old.
The estimator
of a proportion
is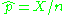
, where X is the number of 'positive' observations (e.g. the number of people out of the n sampled people who are at least 65 years old). When the observations are independent, this estimator has a (scaled) binomial distribution (and is also the sample
mean
of data from a Bernoulli distribution). The maximum variance
of this distribution is 0.25/n, which occurs when the true parameter
is p = 0.5. In practice, since p is unknown, the maximum variance is often used to for sample size assessments.
For sufficiently large n, the distribution of
will be closely approximated by a normal distribution with the same mean and variance. Using this approximation, it can be shown that around 95% of this distribution's probability lies within 2 standard deviations of the mean. Because of this, an interval of the form
will form a 95% confidence interval for the true proportion. If this interval needs to be no more than W units wide, the equation
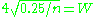
can be solved for n, yielding n = 4/W2 = 1/B2 where B is the error bound on the estimate, i.e., the estimate is usually given as within ± B. So, for B = 10% one requires n = 100, for B = 5% one needs n = 400, for B = 3% the requirement approximates to n = 1000, while for B = 1% a sample size of n = 10000 is required. These numbers are quoted often in news reports of opinion poll
s and other sample surveys.
of the sample mean is:
This expression describes quantitatively how the estimate becomes more precise as the sample size increases. Using the central limit theorem
to justify approximating the sample mean with a normal distribution yields an approximate 95% confidence interval of the form
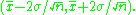
If we wish to have a confidence interval that is W units in width, we would solve
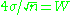
for n, yielding the sample size n = 16σ2/W2.
For example, if we are interested in estimating the amount by which a drug lowers a subject's blood pressure with a confidence interval that is six units wide, and we know that the standard deviation of blood pressure in the population is 15, then the required sample size is 100.
for a test, given a predetermined Type I error rate α. As follows, this can be estimated by pre-determined tables for certain values, by Mead's resource equation, or, more generalized, by the cumulative distribution function
:
The table shown at right can be used to in a two-sample t-test to estimate the sample sizes of an experimental group and a control group that are of equal size, that is, the total number of individuals in the trial is twice that of the number given, and the desired significance level is 0.05. The parameters used are:
All the parameters in the equation are in fact the degrees of freedom
of the number of their concepts, and hence, their numbers are subtracted by 1 before insertion into the equation.
The equation is:
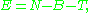
where:
For example, if a study using laboratory animals is planned with four treatment groups (T=3), with eight animals per group, making 32 animals total (N=31), without any further stratification
(B=0), then E would equal 28, which is above the cutoff of 20, indicating that sample size may be a bit too large, and six animals per group might be more appropriate.
:
and an alternative hypothesis:
for some 'smallest significant difference' μ* >0. This is the smallest value for which we care about observing a difference. Now, if we wish to (1) reject H0 with a probability of at least 1-β when
Ha is true (i.e. a power
of 1-β), and (2) reject H0 with probability α when H0 is true, then we need the following:
If zα is the upper α percentage point of the standard normal distribution, then
and so
is a decision rule
which satisfies (2). (Note, this is a 1-tailed test)
Now we wish for this to happen with a probability at least 1-β when
Ha is true. In this case, our sample average will come from a Normal distribution with mean μ*. Therefore we require
Through careful manipulation, this can be shown to happen when
where
is the normal cumulative distribution function
.
, the sample can often be split up into sub-samples. Typically, if there are k such sub-samples (from k different strata) then each of them will have a sample size ni, i = 1, 2, ..., k. These ni must conform to the rule that n1 + n2 + ... + nk = n (i.e. that the total sample size is given by the sum of the sub-sample sizes). Selecting these ni optimally can be done in various ways, using (for example) Neyman's optimal allocation.
There are many reasons to use stratified sampling: to decrease variances of sample estimates, to use partly non-random methods, or to study strata individually.
A useful, partly non-random method would be to sample individuals where easily accessible, but, where not, sample clusters to save travel costs.
In general, for H strata, a weighted sample mean is
with
The weights, W(h), frequently, but not always, represent the proportions of
the population elements in the strata, and W(h)=N(h)/N. For a fixed sample
size, that is n=Sum{n(h)},
which can be made a minimum if the sampling rate
within each stratum is made
proportional to the standard deviation within each stratum: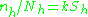
.
An "optimum allocation" is reached when the sampling rates within the strata
are made directly proportional to the standard deviations within the strata
and inversely proportional to the square roots of the costs per element
within the strata:
or, more generally, when
Statistical inference
In statistics, statistical inference is the process of drawing conclusions from data that are subject to random variation, for example, observational errors or sampling variation...
about a population
Statistical population
A statistical population is a set of entities concerning which statistical inferences are to be drawn, often based on a random sample taken from the population. For example, if we were interested in generalizations about crows, then we would describe the set of crows that is of interest...
from a sample. In practice, the sample size used in a study is determined based on the expense of data collection, and the need to have sufficient statistical power
Statistical power
The power of a statistical test is the probability that the test will reject the null hypothesis when the null hypothesis is actually false . The power is in general a function of the possible distributions, often determined by a parameter, under the alternative hypothesis...
. In complicated studies there may be several different sample sizes involved in the study: for example, in as survey sampling
Survey sampling
In statistics, survey sampling describes the process of selecting a sample of elements from a target population in order to conduct a survey.A survey may refer to many different types or techniques of observation, but in the context of survey sampling it most often involves a questionnaire used to...
involving stratified sampling
Stratified sampling
In statistics, stratified sampling is a method of sampling from a population.In statistical surveys, when subpopulations within an overall population vary, it is advantageous to sample each subpopulation independently. Stratification is the process of dividing members of the population into...
there would be different sample sizes for each population. In a census
Census
A census is the procedure of systematically acquiring and recording information about the members of a given population. It is a regularly occurring and official count of a particular population. The term is used mostly in connection with national population and housing censuses; other common...
, data are collected on the entire population, hence the sample size is equal to the population size. In experimental design, where a study may be divided into different treatment groups, there may be different sample sizes for each group.
Sample sizes may be chosen in several different ways:
- expedience - For example, include those items readily available or convenient to collect. A choice of small sample sizes, though sometimes necessary, can result in wide confidence intervalConfidence intervalIn statistics, a confidence interval is a particular kind of interval estimate of a population parameter and is used to indicate the reliability of an estimate. It is an observed interval , in principle different from sample to sample, that frequently includes the parameter of interest, if the...
s or risks of errors in statistical hypothesis testingStatistical hypothesis testingA statistical hypothesis test is a method of making decisions using data, whether from a controlled experiment or an observational study . In statistics, a result is called statistically significant if it is unlikely to have occurred by chance alone, according to a pre-determined threshold...
. - using a target variance for an estimate to be derived from the sample eventually obtained
- using a target for the power of a statistical testStatistical hypothesis testingA statistical hypothesis test is a method of making decisions using data, whether from a controlled experiment or an observational study . In statistics, a result is called statistically significant if it is unlikely to have occurred by chance alone, according to a pre-determined threshold...
to be applied once the sample is collected.
How samples are collected is discussed in sampling (statistics)
Sampling (statistics)
In statistics and survey methodology, sampling is concerned with the selection of a subset of individuals from within a population to estimate characteristics of the whole population....
and survey data collection
Survey data collection
The methods involved in survey data collection are any of a number of ways in which data can be collected for a statistical survey. These are methods that are used to collect information from a sample of individuals in a systematic way....
.
Introduction
Larger sample sizes generally lead to increased precisionAccuracy and precision
In the fields of science, engineering, industry and statistics, the accuracy of a measurement system is the degree of closeness of measurements of a quantity to that quantity's actual value. The precision of a measurement system, also called reproducibility or repeatability, is the degree to which...
when estimating unknown parameters. For example, if we wish to know the proportion of a certain species of fish that is infected with a pathogen, we would generally have a more accurate estimate of this proportion if we sampled and examined 200, rather than 100 fish. Several fundamental facts of mathematical statistics describe this phenomenon, including the law of large numbers
Law of large numbers
In probability theory, the law of large numbers is a theorem that describes the result of performing the same experiment a large number of times...
and the central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
.
In some situations, the increase in accuracy for larger sample sizes is minimal, or even non-existent. This can result from the presence of systematic error
Systematic error
Systematic errors are biases in measurement which lead to the situation where the mean of many separate measurements differs significantly from the actual value of the measured attribute. All measurements are prone to systematic errors, often of several different types...
s or strong dependence in the data, or if the data follow a heavy-tailed distribution.
Sample sizes are judged based on the quality of the resulting estimates. For example, if a proportion is being estimated, one may wish to have the 95% confidence interval
Confidence interval
In statistics, a confidence interval is a particular kind of interval estimate of a population parameter and is used to indicate the reliability of an estimate. It is an observed interval , in principle different from sample to sample, that frequently includes the parameter of interest, if the...
be less than 0.06 units wide. Alternatively, sample size may be assessed based on the power
Statistical power
The power of a statistical test is the probability that the test will reject the null hypothesis when the null hypothesis is actually false . The power is in general a function of the possible distributions, often determined by a parameter, under the alternative hypothesis...
of a hypothesis test. For example, if we are comparing the support for a certain political candidate among women with the support for that candidate among men, we may wish to have 80% power to detect a difference in the support levels of 0.04 units.
Estimating proportions and means
A relatively simple situation is estimation of a proportionProportionality (mathematics)
In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, are proportional if the ratio \tfrac yx is constant. We also say that one...
. For example, we may wish to estimate the proportion of residents in a community who are at least 65 years old.
The estimator
Estimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
of a proportion
Proportionality (mathematics)
In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, are proportional if the ratio \tfrac yx is constant. We also say that one...
is
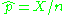, where X is the number of 'positive' observations (e.g. the number of people out of the n sampled people who are at least 65 years old). When the observations are independent, this estimator has a (scaled) binomial distribution (and is also the sampleSample (statistics)
In statistics, a sample is a subset of a population. Typically, the population is very large, making a census or a complete enumeration of all the values in the population impractical or impossible. The sample represents a subset of manageable size...
mean
Arithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
of data from a Bernoulli distribution). The maximum variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of this distribution is 0.25/n, which occurs when the true parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
is p = 0.5. In practice, since p is unknown, the maximum variance is often used to for sample size assessments.
For sufficiently large n, the distribution of
will be closely approximated by a normal distribution with the same mean and variance. Using this approximation, it can be shown that around 95% of this distribution's probability lies within 2 standard deviations of the mean. Because of this, an interval of the formwill form a 95% confidence interval for the true proportion. If this interval needs to be no more than W units wide, the equation
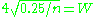
can be solved for n, yielding n = 4/W2 = 1/B2 where B is the error bound on the estimate, i.e., the estimate is usually given as within ± B. So, for B = 10% one requires n = 100, for B = 5% one needs n = 400, for B = 3% the requirement approximates to n = 1000, while for B = 1% a sample size of n = 10000 is required. These numbers are quoted often in news reports of opinion poll
Opinion poll
An opinion poll, sometimes simply referred to as a poll is a survey of public opinion from a particular sample. Opinion polls are usually designed to represent the opinions of a population by conducting a series of questions and then extrapolating generalities in ratio or within confidence...
s and other sample surveys.
Estimation of means
A proportion is a special case of a mean. When estimating the population mean using an independent and identically distributed (iid) sample of size n, where each data value has variance σ2, the standard errorStandard error (statistics)
The standard error is the standard deviation of the sampling distribution of a statistic. The term may also be used to refer to an estimate of that standard deviation, derived from a particular sample used to compute the estimate....
of the sample mean is:
This expression describes quantitatively how the estimate becomes more precise as the sample size increases. Using the central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
to justify approximating the sample mean with a normal distribution yields an approximate 95% confidence interval of the form
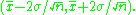
If we wish to have a confidence interval that is W units in width, we would solve
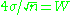
for n, yielding the sample size n = 16σ2/W2.
For example, if we are interested in estimating the amount by which a drug lowers a subject's blood pressure with a confidence interval that is six units wide, and we know that the standard deviation of blood pressure in the population is 15, then the required sample size is 100.
Required sample sizes for hypothesis tests
A common problem facing statisticians is calculating the sample size required to yield a certain powerStatistical power
The power of a statistical test is the probability that the test will reject the null hypothesis when the null hypothesis is actually false . The power is in general a function of the possible distributions, often determined by a parameter, under the alternative hypothesis...
for a test, given a predetermined Type I error rate α. As follows, this can be estimated by pre-determined tables for certain values, by Mead's resource equation, or, more generalized, by the cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
:
By tables
Power Statistical power The power of a statistical test is the probability that the test will reject the null hypothesis when the null hypothesis is actually false . The power is in general a function of the possible distributions, often determined by a parameter, under the alternative hypothesis... | | Cohen's d | ||
|---|---|---|---|
| 0.2 | 0.5 | 0.8 | |
| 0.25 | 84 | 14 | 6 |
| 0.50 | 193 | 32 | 13 |
| 0.60 | 246 | 40 | 16 |
| 0.70 | 310 | 50 | 20 |
| 0.80 | 393 | 64 | 26 |
| 0.90 | 526 | 85 | 34 |
| 0.95 | 651 | 105 | 42 |
| 0.99 | 920 | 148 | 58 |
The table shown at right can be used to in a two-sample t-test to estimate the sample sizes of an experimental group and a control group that are of equal size, that is, the total number of individuals in the trial is twice that of the number given, and the desired significance level is 0.05. The parameters used are:
- The desired statistical powerStatistical powerThe power of a statistical test is the probability that the test will reject the null hypothesis when the null hypothesis is actually false . The power is in general a function of the possible distributions, often determined by a parameter, under the alternative hypothesis...
of the trial, shown in column to the left. - Cohen's d, which is the expected difference between the meanMeanIn statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
s of the target values between the experimental group and the control group, divided by the expected standard deviationStandard deviationStandard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
.
Mead's resource equation
Mead's resource equation is often used for estimating sample sizes of laboratory animals, as well as in many other laboratory experiments. It may not be as accurate as using other methods in estimating sample size, but gives a hint of what is the appropriate sample size where parameters such as expected standard deviations or expected differences in values between groups are unknown or very hard to estimate.All the parameters in the equation are in fact the degrees of freedom
Degrees of freedom
Degrees of freedom can mean:* Degrees of freedom , independent displacements and/or rotations that specify the orientation of the body or system...
of the number of their concepts, and hence, their numbers are subtracted by 1 before insertion into the equation.
The equation is:
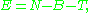
where:
- N is the total number of individuals or units in the study (minus 1)
- B is the blocking component, representing environmental effects allowed for in the design (minus 1)
- T is the treatment component, corresponding to the number of treatment groupsTreatment groupsIn the design of experiments, treatments are applied to experimental units in the treatment group, while no treatments would be applied to members of a control group....
(including control group) being used, or the number of questions being asked (minus 1) - E is the degrees of freedom of the error component, and should be somewhere between 10 and 20.
For example, if a study using laboratory animals is planned with four treatment groups (T=3), with eight animals per group, making 32 animals total (N=31), without any further stratification
Stratified sampling
In statistics, stratified sampling is a method of sampling from a population.In statistical surveys, when subpopulations within an overall population vary, it is advantageous to sample each subpopulation independently. Stratification is the process of dividing members of the population into...
(B=0), then E would equal 28, which is above the cutoff of 20, indicating that sample size may be a bit too large, and six animals per group might be more appropriate.
By cumulative distribution function
Let Xi, i = 1, 2, ..., n be independent observations taken from a normal distribution with unknown mean μ and known variance σ2. Let us consider two hypotheses, a null hypothesisNull hypothesis
The practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
:
and an alternative hypothesis:
for some 'smallest significant difference' μ* >0. This is the smallest value for which we care about observing a difference. Now, if we wish to (1) reject H0 with a probability of at least 1-β when
Ha is true (i.e. a power
Statistical power
The power of a statistical test is the probability that the test will reject the null hypothesis when the null hypothesis is actually false . The power is in general a function of the possible distributions, often determined by a parameter, under the alternative hypothesis...
of 1-β), and (2) reject H0 with probability α when H0 is true, then we need the following:
If zα is the upper α percentage point of the standard normal distribution, then
and so
- 'Reject H0 if our sample average (
) is more than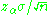 
'
is a decision rule
Decision rule
In decision theory, a decision rule is a function which maps an observation to an appropriate action. Decision rules play an important role in the theory of statistics and economics, and are closely related to the concept of a strategy in game theory....
which satisfies (2). (Note, this is a 1-tailed test)
Now we wish for this to happen with a probability at least 1-β when
Ha is true. In this case, our sample average will come from a Normal distribution with mean μ*. Therefore we require
Through careful manipulation, this can be shown to happen when
where
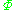is the normal cumulative distribution functionCumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
.
Stratified sample size
With more complicated sampling techniques, such as stratified samplingStratified sampling
In statistics, stratified sampling is a method of sampling from a population.In statistical surveys, when subpopulations within an overall population vary, it is advantageous to sample each subpopulation independently. Stratification is the process of dividing members of the population into...
, the sample can often be split up into sub-samples. Typically, if there are k such sub-samples (from k different strata) then each of them will have a sample size ni, i = 1, 2, ..., k. These ni must conform to the rule that n1 + n2 + ... + nk = n (i.e. that the total sample size is given by the sum of the sub-sample sizes). Selecting these ni optimally can be done in various ways, using (for example) Neyman's optimal allocation.
There are many reasons to use stratified sampling: to decrease variances of sample estimates, to use partly non-random methods, or to study strata individually.
A useful, partly non-random method would be to sample individuals where easily accessible, but, where not, sample clusters to save travel costs.
In general, for H strata, a weighted sample mean is
with
The weights, W(h), frequently, but not always, represent the proportions of
the population elements in the strata, and W(h)=N(h)/N. For a fixed sample
size, that is n=Sum{n(h)},
which can be made a minimum if the sampling rate
Sampling rate
The sampling rate, sample rate, or sampling frequency defines the number of samples per unit of time taken from a continuous signal to make a discrete signal. For time-domain signals, the unit for sampling rate is hertz , sometimes noted as Sa/s...
within each stratum is made
proportional to the standard deviation within each stratum:
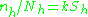.An "optimum allocation" is reached when the sampling rates within the strata
are made directly proportional to the standard deviations within the strata
and inversely proportional to the square roots of the costs per element
within the strata:
or, more generally, when
See also
- Degrees of freedom (statistics)Degrees of freedom (statistics)In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
- Design of experimentsDesign of experimentsIn general usage, design of experiments or experimental design is the design of any information-gathering exercises where variation is present, whether under the full control of the experimenter or not. However, in statistics, these terms are usually used for controlled experiments...
- Replication (statistics)Replication (statistics)In engineering, science, and statistics, replication is the repetition of an experimental condition so that the variability associated with the phenomenon can be estimated. ASTM, in standard E1847, defines replication as "the repetition of the set of all the treatment combinations to be compared in...
- Sampling (statistics)Sampling (statistics)In statistics and survey methodology, sampling is concerned with the selection of a subset of individuals from within a population to estimate characteristics of the whole population....
- Statistical powerStatistical powerThe power of a statistical test is the probability that the test will reject the null hypothesis when the null hypothesis is actually false . The power is in general a function of the possible distributions, often determined by a parameter, under the alternative hypothesis...
- Stratified SamplingStratified samplingIn statistics, stratified sampling is a method of sampling from a population.In statistical surveys, when subpopulations within an overall population vary, it is advantageous to sample each subpopulation independently. Stratification is the process of dividing members of the population into...
- Engineering response surface example under Stepwise regressionStepwise regressionIn statistics, stepwise regression includes regression models in which the choice of predictive variables is carried out by an automatic procedure...
.
Further reading
- NIST: Selecting Sample Sizes
- Raven Analytics: Sample Size Calculations
- ASTM E122-07: Standard Practice for Calculating Sample Size to Estimate, With Specified Precision, the Average for a Characteristic of a Lot or Process