
Separation axiom
Encyclopedia
In topology
and related fields of mathematics
, there are several restrictions that one often makes on the kinds of topological space
s that one wishes to consider. Some of these restrictions are given by the separation axioms. These are sometimes called Tychonoff separation axioms, after Andrey Tychonoff.
The separation axioms are axiom
s only in the sense that, when defining the notion of topological space
, one could add these conditions as extra axioms to get a more restricted notion of what a topological space is. The modern approach is to fix once and for all the axiomatization of topological space and then speak of kinds of topological spaces.
However, the term "separation axiom" has stuck. The separation axioms are denoted with the letter "T" after the German
Trennungsaxiom, which means separation axiom.
The precise meanings of the terms associated with the separation axioms has varied over time, as explained in History of the separation axioms
. Especially when reading older literature, be sure to get the authors' definition of each condition mentioned to make sure that you know exactly what they mean.
s. (But separated sets are not the same as separated spaces, defined in the next section.)
The separation axioms are about the use of topological means to distinguish disjoint sets and distinct points. It's not enough for elements of a topological space to be distinct; we may want them to be topologically distinguishable. Similarly, it's not enough for subset
s of a topological space to be disjoint; we may want them to be separated (in any of various ways). The separation axioms all say, in one way or another, that points or sets that are distinguishable or separated in some weak sense must also be distinguishable or separated in some stronger sense.
Let X be a topological space. Then two points x and y in X are topologically distinguishable if they do not have exactly the same neighbourhood
s; that is, at least one of them has a neighbourhood that is not a neighbourhood of the other. If x and y are topologically distinguishable points, then the singleton sets {x} and {y} must be disjoint.
Two points x and y are separated if each of them has a neighbourhood that is not a neighbourhood of the other; that is, neither belongs to the other's closure. More generally, two subsets A and B of X are separated if each is disjoint from the other's closure
. (The closures themselves do not have to be disjoint.) The points x and y are separated if and only if their singleton sets {x} and {y} are separated; all of the remaining conditions for sets may also be applied to points (or to a point and a set) by using singleton sets.
To continue, subsets A and B are separated by neighbourhoods if they have disjoint neighbourhoods. They are separated by closed neighbourhoods if they have disjoint closed neighbourhoods. They are separated by a function if there exists a continuous function
f from the space X to the real line
R such that the image f(A) equals {0} and f(B) equals {1}. Finally, they are precisely separated by a function if there exists a continuous function f from X to R such that the preimage f -1({0}) equals A and f -1({1}) equals B.
These conditions are given in order of increasing strength:
Any two topologically distinguishable points must be distinct, and any two separated points must be topologically distinguishable. Furthermore, any two separated sets must be disjoint, any two sets separated by neighbourhoods must be separated, and so on.
For more on these conditions (including their use outside the separation axioms),
see the articles Separated sets
and Topological distinguishability.
Many of these names have alternative meanings in some of mathematical literature, as explained on History of the separation axioms
; for example, the meanings of "normal" and "T4" are sometimes interchanged, similarly "regular" and "T3", etc. Many of the concepts also have several names; however, the one listed first is always least likely to be ambiguous.
Most of these axioms have alternative definitions with the same meaning; the definitions given here fall into a consistent pattern that relates the various notions of separation defined in the previous section. Other possible definitions can be found in the individual articles.
In all of the following definitions, X is again a topological space
, and all functions are supposed to be continuous.
In this table, you go from the right side to the left side by adding the requirement of T0, and you go from the left side to the right side by removing that requirement, using the Kolmogorov quotient operation. (The names in parentheses given on the left side of this table are generally ambiguous or at least less well known; but they are used in the diagram below.)
Other than the inclusion or exclusion of T0, the relationships between the separation axioms are indicated in the following diagram:
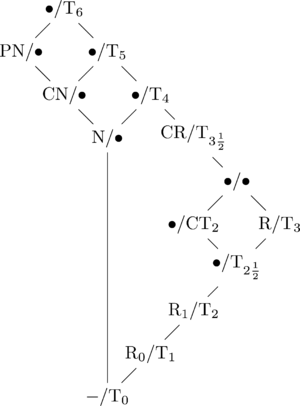 In this diagram, the non-T0 version of a condition is on the left side of the slash, and the T0 version is on the right side. Letters are used for abbreviation
In this diagram, the non-T0 version of a condition is on the left side of the slash, and the T0 version is on the right side. Letters are used for abbreviation
as follows:
"P" = "perfectly", "C" = "completely", "N" = "normal", and "R" (without a subscript) = "regular".
A bullet indicates that there is no special name for a space at that spot. The dash at the bottom indicates no condition.
You can combine two properties using this diagram by following the diagram upwards until both branches meet. For example, if a space is both completely normal ("CN") and completely Hausdorff ("CT2"), then following both branches up, you find the spot "•/T5".
Since completely Hausdorff spaces are T0 (even though completely normal spaces may not be), you take the T0 side of the slash, so a completely normal completely Hausdorff space is the same as a T5 space (less ambiguously known as a completely normal Hausdorff space, as you can see in the table above).
As you can see from the diagram, normal and R0 together imply a host of other properties, since combining the two properties leads you to follow a path through the many nodes on the rightside branch. Since regularity is the most well known of these, spaces that are both normal and R0 are typically called "normal regular spaces". In a somewhat similar fashion, spaces that are both normal and T1 are often called "normal Hausdorff spaces" by people that wish to avoid the ambiguous "T" notation. These conventions can be generalised to other regular spaces and Hausdorff spaces.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and related fields of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, there are several restrictions that one often makes on the kinds of topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s that one wishes to consider. Some of these restrictions are given by the separation axioms. These are sometimes called Tychonoff separation axioms, after Andrey Tychonoff.
The separation axioms are axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s only in the sense that, when defining the notion of topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, one could add these conditions as extra axioms to get a more restricted notion of what a topological space is. The modern approach is to fix once and for all the axiomatization of topological space and then speak of kinds of topological spaces.
However, the term "separation axiom" has stuck. The separation axioms are denoted with the letter "T" after the German
German language
German is a West Germanic language, related to and classified alongside English and Dutch. With an estimated 90 – 98 million native speakers, German is one of the world's major languages and is the most widely-spoken first language in the European Union....
Trennungsaxiom, which means separation axiom.
The precise meanings of the terms associated with the separation axioms has varied over time, as explained in History of the separation axioms
History of the separation axioms
In general topology, the separation axioms have had a convoluted history, with many competing meanings for the same term, and many competing terms for the same concept.- Origins :...
. Especially when reading older literature, be sure to get the authors' definition of each condition mentioned to make sure that you know exactly what they mean.
Preliminary definitions
Before we define the separation axioms themselves, we give concrete meaning to the concept of separated sets (and points) in topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s. (But separated sets are not the same as separated spaces, defined in the next section.)
The separation axioms are about the use of topological means to distinguish disjoint sets and distinct points. It's not enough for elements of a topological space to be distinct; we may want them to be topologically distinguishable. Similarly, it's not enough for subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of a topological space to be disjoint; we may want them to be separated (in any of various ways). The separation axioms all say, in one way or another, that points or sets that are distinguishable or separated in some weak sense must also be distinguishable or separated in some stronger sense.
Let X be a topological space. Then two points x and y in X are topologically distinguishable if they do not have exactly the same neighbourhood
Neighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
s; that is, at least one of them has a neighbourhood that is not a neighbourhood of the other. If x and y are topologically distinguishable points, then the singleton sets {x} and {y} must be disjoint.
Two points x and y are separated if each of them has a neighbourhood that is not a neighbourhood of the other; that is, neither belongs to the other's closure. More generally, two subsets A and B of X are separated if each is disjoint from the other's closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
. (The closures themselves do not have to be disjoint.) The points x and y are separated if and only if their singleton sets {x} and {y} are separated; all of the remaining conditions for sets may also be applied to points (or to a point and a set) by using singleton sets.
To continue, subsets A and B are separated by neighbourhoods if they have disjoint neighbourhoods. They are separated by closed neighbourhoods if they have disjoint closed neighbourhoods. They are separated by a function if there exists a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
f from the space X to the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
R such that the image f(A) equals {0} and f(B) equals {1}. Finally, they are precisely separated by a function if there exists a continuous function f from X to R such that the preimage f -1({0}) equals A and f -1({1}) equals B.
These conditions are given in order of increasing strength:
Any two topologically distinguishable points must be distinct, and any two separated points must be topologically distinguishable. Furthermore, any two separated sets must be disjoint, any two sets separated by neighbourhoods must be separated, and so on.
For more on these conditions (including their use outside the separation axioms),
see the articles Separated sets
Separated sets
In topology and related branches of mathematics, separated sets are pairs of subsets of a given topological space that are related to each other in a certain way....
and Topological distinguishability.
Main definitions
These definitions all use essentially the preliminary definitions above.Many of these names have alternative meanings in some of mathematical literature, as explained on History of the separation axioms
History of the separation axioms
In general topology, the separation axioms have had a convoluted history, with many competing meanings for the same term, and many competing terms for the same concept.- Origins :...
; for example, the meanings of "normal" and "T4" are sometimes interchanged, similarly "regular" and "T3", etc. Many of the concepts also have several names; however, the one listed first is always least likely to be ambiguous.
Most of these axioms have alternative definitions with the same meaning; the definitions given here fall into a consistent pattern that relates the various notions of separation defined in the previous section. Other possible definitions can be found in the individual articles.
In all of the following definitions, X is again a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, and all functions are supposed to be continuous.
- X is T0, or Kolmogorov, if any two distinct points in X are topologically distinguishable. (It will be a common theme among the separation axioms to have one version of an axiom that requires T0 and one version that doesn't.)
- X is R0, or symmetric, if any two topologically distinguishable points in X are separated.
- X is T1T1 spaceIn topology and related branches of mathematics, a T1 space is a topological space in which, for every pair of distinct points, each has an open neighborhood not containing the other. An R0 space is one in which this holds for every pair of topologically distinguishable points...
, or accessible or Fréchet, if any two distinct points in X are separated. Thus, X is T1 if and only if it is both T0 and R0. (Although you may say such things as "T1 space", "Fréchet topology", and "Suppose that the topological space X is Fréchet", avoid saying "Fréchet space" in this context, since there is another entirely different notion of Fréchet spaceFréchet spaceIn functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces...
in functional analysisFunctional analysisFunctional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
.)
- X is R1, or preregular, if any two topologically distinguishable points in X are separated by neighbourhoods. An R1 space must also be R0.
- X is HausdorffHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
, or T2 or separated, if any two distinct points in X are separated by neighbourhoods. Thus, X is Hausdorff if and only if it is both T0 and R1. A Hausdorff space must also be T1.
- X is T2½, or Urysohn, if any two distinct points in X are separated by closed neighbourhoods. A T2½ space must also be Hausdorff.
- X is completely HausdorffCompletely Hausdorff spaceIn topology, an Urysohn space, or T2½ space, is a topological space in which any two distinct points can be separated by closed neighborhoods. A completely Hausdorff space, or functionally Hausdorff space, is a topological space in which any two distinct points can be separated by a continuous...
, or completely T2, if any two distinct points in X are separated by a function. A completely Hausdorff space must also be T2½.
- X is regularRegular spaceIn topology and related fields of mathematics, a topological space X is called a regular space if every non-empty closed subset C of X and a point p not contained in C admit non-overlapping open neighborhoods. Thus p and C...
if, given any point x and closed set F in X, if x does not belong to F, then they are separated by neighbourhoods. (In fact, in a regular space, any such x and F will also be separated by closed neighbourhoods.) A regular space must also be R1.
- X is regular Hausdorff, or T3, if it is both T0 and regular. A regular Hausdorff space must also be T2½.
- X is completely regular if, given any point x and closed set F in X, if x does not belong to F, then they are separated by a function. A completely regular space must also be regular.
- X is TychonoffTychonoff spaceIn topology and related branches of mathematics, Tychonoff spaces and completely regular spaces are kinds of topological spaces.These conditions are examples of separation axioms....
, or T3½, completely T3, or completely regular Hausdorff, if it is both T0 and completely regular. A Tychonoff space must also be both regular Hausdorff and completely Hausdorff.
- X is normalNormal spaceIn topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
if any two disjoint closed subsets of X are separated by neighbourhoods. (In fact, in a normal space, any two disjoint closed sets will also be separated by a function; this is Urysohn's lemmaUrysohn's lemmaIn topology, Urysohn's lemma is a lemma that states that a topological space is normal if and only if any two disjoint closed subsets can be separated by a function....
.)
- X is normal Hausdorff, or T4, if it is both T1 and normal. A normal Hausdorff space must also be both Tychonoff and normal regular.
- X is completely normal if any two separated sets are separated by neighbourhoods. A completely normal space must also be normal.
- X is completely normal Hausdorff, or T5 or completely T4, if it is both completely normal and T1. A completely normal Hausdorff space must also be normal Hausdorff.
- X is perfectly normal if any two disjoint closed sets are precisely separated by a function. A perfectly normal space must also be completely normal.
- X is perfectly normal Hausdorff, or T6 or perfectly T4, if it is both perfectly normal and T1. A perfectly normal Hausdorff space must also be completely normal Hausdorff.
Relationships between the axioms
The T0 axiom is special in that it can not only be added to a property (so that completely regular plus T0 is Tychonoff) but also subtracted from a property (so that Hausdorff minus T0 is R1), in a fairly precise sense; see Kolmogorov quotient for more information. When applied to the separation axioms, this leads to the relationships in the table below:| T0 version | Non-T0 version |
|---|---|
| T0 | (No requirement) |
| T1 | R0 |
| Hausdorff (T2) | R1 |
| T2½ | (No special name) |
| Completely Hausdorff | (No special name) |
| Regular Hausdorff (T3) | Regular |
| Tychonoff (T3½) | Completely regular |
| Normal T0 | Normal |
| Normal Hausdorff (T4) | Normal regular |
| Completely normal T0 | Completely normal |
| Completely normal Hausdorff (T5) | Completely normal regular |
| Perfectly normal T0 | Perfectly normal |
| Perfectly normal Hausdorff (T6) | Perfectly normal regular |
In this table, you go from the right side to the left side by adding the requirement of T0, and you go from the left side to the right side by removing that requirement, using the Kolmogorov quotient operation. (The names in parentheses given on the left side of this table are generally ambiguous or at least less well known; but they are used in the diagram below.)
Other than the inclusion or exclusion of T0, the relationships between the separation axioms are indicated in the following diagram:

Abbreviation
An abbreviation is a shortened form of a word or phrase. Usually, but not always, it consists of a letter or group of letters taken from the word or phrase...
as follows:
"P" = "perfectly", "C" = "completely", "N" = "normal", and "R" (without a subscript) = "regular".
A bullet indicates that there is no special name for a space at that spot. The dash at the bottom indicates no condition.
You can combine two properties using this diagram by following the diagram upwards until both branches meet. For example, if a space is both completely normal ("CN") and completely Hausdorff ("CT2"), then following both branches up, you find the spot "•/T5".
Since completely Hausdorff spaces are T0 (even though completely normal spaces may not be), you take the T0 side of the slash, so a completely normal completely Hausdorff space is the same as a T5 space (less ambiguously known as a completely normal Hausdorff space, as you can see in the table above).
As you can see from the diagram, normal and R0 together imply a host of other properties, since combining the two properties leads you to follow a path through the many nodes on the rightside branch. Since regularity is the most well known of these, spaces that are both normal and R0 are typically called "normal regular spaces". In a somewhat similar fashion, spaces that are both normal and T1 are often called "normal Hausdorff spaces" by people that wish to avoid the ambiguous "T" notation. These conventions can be generalised to other regular spaces and Hausdorff spaces.
Other separation axioms
There are some other conditions on topological spaces that are sometimes classified with the separation axioms, but these don't fit in with the usual separation axioms as completely. Other than their definitions, they aren't discussed here; see their individual articles.- X is semiregularSemiregular spaceA semiregular space is a topological space whose regular open sets form a base.Every regular space is semiregular, and every topological space may be embedded into a semiregular space....
if the regular open sets form a baseBase (topology)In mathematics, a base B for a topological space X with topology T is a collection of open sets in T such that every open set in T can be written as a union of elements of B. We say that the base generates the topology T...
for the open sets of X. Any regular space must also be semiregular. - X is quasi-regular if for any nonempty open set G, there is a nonempty open set H such that the closure of H is contained in G.
- X is fully normal if every open cover has an open star refinementStar refinementIn mathematics, specifically in the study of topology and open covers of a topological space X, a star refinement is a particular kind of refinement of an open cover of X....
. X is fully T4, or fully normal Hausdorff, if it is both T1 and fully normal. Every fully normal space is normal and every fully T4 space is T4. Moreover, one can show that every fully T4 space is paracompact. In fact, fully normal spaces actually have more to do with paracompactness than with the usual separation axioms. - X is soberSober spaceIn mathematics, a sober space is a topological spacesuch that every irreducible closed subset of X is the closure of exactly one point of X: that is, has a unique generic point.-Properties and examples :...
if, for every closed set C that is not the (possibly nondisjoint) union of two smaller closed sets, there is a unique point p such that the closure of {p} equals C. More briefly, every irreducible closed set has a unique generic point. Any Hausdorff space must be sober, and any sober space must be T0.
Sources
-
- has Ri axioms (among others)
- Stephen Willard, General Topology, Addison-Wesley, 1970. Reprinted by Dover Publications, New York, 2004. ISBN 0-486-43479-6 (Dover edition).
- has all of the non-Ri axioms mentioned in this article, with these definitions
- There are several other good books on general topologyGeneral topologyIn mathematics, general topology or point-set topology is the branch of topology which studies properties of topological spaces and structures defined on them...
, but beware that some use slightly different definitions.

