Identity (mathematics)
Encyclopedia
In mathematics
, the term identity has several different important meanings:
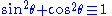
which is true for all complex
values of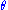
(since the complex numbers 
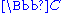are the domain of sin and cos), as opposed to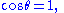
which is true only for some values of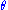
, not all. For example, the latter equation is true when 
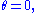false when 
.
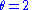See also list of mathematical identities.
.
The number 0 is the "additive identity" for integers, real numbers, and complex numbers. For the real numbers, for all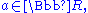
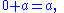
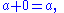and
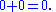
Similarly, The number 1 is the "multiplicative identity" for integers, real numbers, and complex numbers. For the real numbers, for all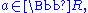
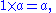
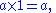and
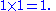
, which sends each element of the set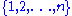
to itself or 
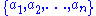to itself in natural order.
of permutations of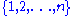
under composition
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the term identity has several different important meanings:
- An identity is a relation which is tautologicallyTautology (logic)In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of the involved variables. Definitions are often indicated by the 'triple barTriple barThe triple bar, ≡, is a symbol used in formal logic. It has the appearance of a "=" sign with a third line.Logically, it has a similar meaning to the if and only if coupler ⇔...
' symbol ≡, such as A2 ≡ x·x. The symbol ≡ can also be used with other meanings, but these can usually be interpreted in some way as a definition, or something which is otherwise tautologically true (for example, a congruence relationCongruence relationIn abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
).
- In algebraAlgebraAlgebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, an identity or identity elementIdentity elementIn mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
of a set S with a binary operationBinary operationIn mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
· is an element e that, when combined with any element x of S, produces that same x. That is, for all x in S. An example of this is the identity matrixIdentity matrixIn linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
.
- The identity functionIdentity functionIn mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
from a set S to itself, often denoted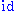
or 
, is the function which maps every element to itself. In other words,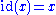 
for all x in S. This function serves as the identity element in the set of all functions from S to itself with respect to function compositionFunction compositionIn mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
.
Identity relation
A common example of the first meaning is the trigonometric identity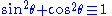which is true for all complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
values of
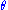(since the complex numbers 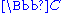are the domain of sin and cos), as opposed to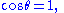which is true only for some values of
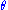, not all. For example, the latter equation is true when 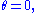false when 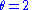.See also list of mathematical identities.
Identity element
The concepts of "additive identity" and "multiplicative identity" are central to the Peano axiomsPeano axioms
In mathematical logic, the Peano axioms, also known as the Dedekind–Peano axioms or the Peano postulates, are a set of axioms for the natural numbers presented by the 19th century Italian mathematician Giuseppe Peano...
.
The number 0 is the "additive identity" for integers, real numbers, and complex numbers. For the real numbers, for all
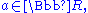
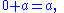
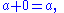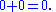
andSimilarly, The number 1 is the "multiplicative identity" for integers, real numbers, and complex numbers. For the real numbers, for all
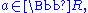
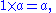
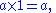and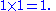Identity function
A common example of an identity function is the identity permutationPermutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
, which sends each element of the set
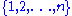to itself or 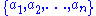to itself in natural order.Comparison
These meanings are not mutually exclusive; for instance, the identity permutation is the identity element in the groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of permutations of
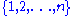under compositionFunction composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
.
External links
- A Collection of Algebraic Identities
- EquationSolver – A webpage that can test a suggested identity and return a true/false "verdict".