Kazhdan's property (T)
Encyclopedia
In mathematics
, a locally compact topological group
G has property (T) if the trivial representation
is an isolated point
in its unitary dual equipped with the Fell topology. Informally, this means that if G acts unitarily
on a Hilbert space
and has "almost invariant vectors", then it has a nonzero invariant vector. The formal definition, introduced by David Kazhdan
(1967), gives this a precise, quantitative meaning.
Although originally defined in terms of irreducible representations, property (T) can often be checked even when there is little or no explicit knowledge of the unitary dual. Property (T) has important applications to group representation theory, lattices in algebraic groups over local fields
, ergodic theory
, geometric group theory
, expanders
, operator algebras and the theory of networks.
and π : G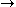
U(H) a unitary representation
of G on a (complex) Hilbert space H. If ε > 0 and K is a compact subset of G, then a unit vector ξ in H is called an (ε, K)-invariant vector if π(g) ξ - ξ < ε for all g in K.
The following conditions on G are all equivalent to G having property (T) of Kazhdan
, and any of them can be used as the definition of property (T).
(1) The trivial representation
is an isolated point
of the unitary dual of G with Fell topology.
(2) Any sequence of continuous
positive definite functions
on G converging to 1 uniformly on compact subsets, converges to 1 uniformly on G.
(3) Every unitary representation
of G that has an (ε, K)-invariant unit vector for any ε > 0 and any compact subset K, has a non-zero invariant vector.
(4) There exists an ε > 0 and a compact subset K of G such that every unitary representation of G that has an (ε, K)-invariant unit vector, has a nonzero invariant vector.
(5) Every continuous affine
isometric
action
of G on a real Hilbert space
has a fixed point (property (FH)).
If H is a closed subgroup of G, the pair (G,H) is said to have relative property (T) of Margulis if there exists an ε > 0 and a compact subset K of G such that whenever a unitary representation of G has an (ε, K)-invariant unit vector, then it has a non-zero vector fixed by H.
The equivalence of (4) and (5) (Property (FH)) is the Delorme-Guichardet Theorem. The fact that (5) implies (4) requires us to assume that G is σ-compact (and locally compact) (Bekka et al., Theorem 2.12.4).
Examples of groups that do not have property (T) include
by embedding them as lattices in real or p-adic Lie groups with property (T). There are now several direct methods available.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a locally compact topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
G has property (T) if the trivial representation
Trivial representation
In the mathematical field of representation theory, a trivial representation is a representation of a group G on which all elements of G act as the identity mapping of V...
is an isolated point
Isolated point
In topology, a branch of mathematics, a point x of a set S is called an isolated point of S, if there exists a neighborhood of x not containing other points of S.In particular, in a Euclidean space ,...
in its unitary dual equipped with the Fell topology. Informally, this means that if G acts unitarily
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
and has "almost invariant vectors", then it has a nonzero invariant vector. The formal definition, introduced by David Kazhdan
David Kazhdan
David Kazhdan or Každan, Kazhdan, formerly named Dmitry Aleksandrovich Kazhdan , is a Soviet and Israeli mathematician known for work in representation theory.-Life:...
(1967), gives this a precise, quantitative meaning.
Although originally defined in terms of irreducible representations, property (T) can often be checked even when there is little or no explicit knowledge of the unitary dual. Property (T) has important applications to group representation theory, lattices in algebraic groups over local fields
Grigory Margulis
Gregori Aleksandrovich Margulis is a Russian mathematician known for his far-reaching work on lattices in Lie groups, and the introduction of methods from ergodic theory into diophantine approximation. He was awarded a Fields Medal in 1978 and a Wolf Prize in Mathematics in 2005, becoming the...
, ergodic theory
Ergodic theory
Ergodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
, geometric group theory
Geometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
, expanders
Expander graph
In combinatorics, an expander graph is a sparse graph that has strong connectivity properties, quantified using vertex, edge or spectral expansion as described below...
, operator algebras and the theory of networks.
Definitions
Let G be a σ-compact, locally compact topological groupTopological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
and π : G
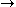U(H) a unitary representationUnitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
of G on a (complex) Hilbert space H. If ε > 0 and K is a compact subset of G, then a unit vector ξ in H is called an (ε, K)-invariant vector if π(g) ξ - ξ < ε for all g in K.
The following conditions on G are all equivalent to G having property (T) of Kazhdan
David Kazhdan
David Kazhdan or Každan, Kazhdan, formerly named Dmitry Aleksandrovich Kazhdan , is a Soviet and Israeli mathematician known for work in representation theory.-Life:...
, and any of them can be used as the definition of property (T).
(1) The trivial representation
Trivial representation
In the mathematical field of representation theory, a trivial representation is a representation of a group G on which all elements of G act as the identity mapping of V...
is an isolated point
Isolated point
In topology, a branch of mathematics, a point x of a set S is called an isolated point of S, if there exists a neighborhood of x not containing other points of S.In particular, in a Euclidean space ,...
of the unitary dual of G with Fell topology.
(2) Any sequence of continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
positive definite functions
Positive definite function on a group
In operator theory, a positive-definite function on a group relates the notions of positivity, in the context of Hilbert spaces, and algebraic groups...
on G converging to 1 uniformly on compact subsets, converges to 1 uniformly on G.
(3) Every unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
of G that has an (ε, K)-invariant unit vector for any ε > 0 and any compact subset K, has a non-zero invariant vector.
(4) There exists an ε > 0 and a compact subset K of G such that every unitary representation of G that has an (ε, K)-invariant unit vector, has a nonzero invariant vector.
(5) Every continuous affine
Affine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
isometric
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of G on a real Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
has a fixed point (property (FH)).
If H is a closed subgroup of G, the pair (G,H) is said to have relative property (T) of Margulis if there exists an ε > 0 and a compact subset K of G such that whenever a unitary representation of G has an (ε, K)-invariant unit vector, then it has a non-zero vector fixed by H.
Discussion
Clearly, definition (4) implies definition (3). Let us show the converse, assuming local compactness. So let G be a locally compact group satisfying (3). By Theorem 1.3.1 of Bekka et al., G is compactly generated. Therefore, Remark 1.1.2(v) of Bekka et al. tells us the following. If we take K to be a compact generating set of G, and let ε be any positive real number, then a unitary representation of G having an (ε, K)-invariant unit vector has (ε', K ')-invariant unit vectors for every ε' > 0 and K ' compact. Therefore, by (3), such a representation of G will have a nonzero invariant vector, establishing (4).The equivalence of (4) and (5) (Property (FH)) is the Delorme-Guichardet Theorem. The fact that (5) implies (4) requires us to assume that G is σ-compact (and locally compact) (Bekka et al., Theorem 2.12.4).
General properties
- Property (T) is preserved under quotients: if G has property (T) and H is a quotient groupQuotient groupIn mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
of G then H has property (T). Equivalently, if a homomorphic image of a group G does not have property (T) then G itself does not have property (T). - If G has property (T) then G/
[ G, G] is compact. - Any countable discrete group with property (T) is finitely generated.
- An amenable groupAmenable groupIn mathematics, an amenable group is a locally compact topological group G carrying a kind of averaging operation on bounded functions that is invariant under translation by group elements...
which has property (T) is necessarily compactCompact groupIn mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
. Amenability and property (T) are in a rough sense opposite: they make almost invariant vectors easy or hard to find. - Kazhdan's theorem: If Γ is a latticeLattice (discrete subgroup)In Lie theory and related areas of mathematics, a lattice in a locally compact topological group is a discrete subgroup with the property that the quotient space has finite invariant measure...
in a Lie group G then Γ has property (T) if and only if G has property (T). Thus for n ≥ 3, the special linear group SLn(Z) has property (T).
Examples
- Compact topological groups have property (T). In particular, the circle group, the additive group Zp of p-adic integers, compact special unitary groupSpecial unitary groupThe special unitary group of degree n, denoted SU, is the group of n×n unitary matrices with determinant 1. The group operation is that of matrix multiplication...
s SU(n) and all finite groups have property (T). - SimpleSimple Lie groupIn group theory, a simple Lie group is a connected non-abelian Lie group G which does not have nontrivial connected normal subgroups.A simple Lie algebra is a non-abelian Lie algebra whose only ideals are 0 and itself...
real Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s of real rank at least two have property (T). This family of groups includes the special linear groupSpecial linear groupIn mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
s SLn(R) for n ≥ 3 and the special orthogonal groupOrthogonal groupIn mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
s SO(p,q) for p > q ≥ 2 and SO(p,p) for p ≥ 3. More generally, this holds for simple algebraic groupAlgebraic groupIn algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
s of rank at least two over a local fieldLocal fieldIn mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
. - The pairs (Rn
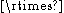SLn(R), Rn) and (Zn
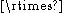SLn(Z), Zn) have relative property (T) for n ≥ 2. - For n ≥ 2, the noncompact Lie group Sp(n,1) of isometries of a quaternionQuaternionIn mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
ic hermitian form of signature (n,1) is a simple Lie group of real rank 1 that has property (T). By Kazhdan's theorem, lattices in this group have property (T). This construction is significant because these lattices are hyperbolic groupHyperbolic groupIn group theory, a hyperbolic group, also known as a word hyperbolic group, Gromov hyperbolic group, negatively curved group is a finitely generated group equipped with a word metric satisfying certain properties characteristic of hyperbolic geometry. The notion of a hyperbolic group was introduced...
s; thus, there are groups that are hyperbolic and have property (T). Explicit examples of groups in this category are provided by arithmetic lattices in Sp(n,1) and certain quaternionic reflection groupReflection groupIn group theory and geometry, a reflection group is a discrete group which is generated by a set of reflections of a finite-dimensional Euclidean space. The symmetry group of a regular polytope or of a tiling of the Euclidean space by congruent copies of a regular polytope is necessarily a...
s.
Examples of groups that do not have property (T) include
- The additive groups of integers Z, of real numbers R and of p-adic numbers Qp.
- The special linear groups SL2(Z) and SL2(R), although SL2 has property (τ) with respect to principal congruence subgroups, by Selberg's theorem.
- Noncompact solvable groupSolvable groupIn mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
s. - Nontrivial free groupFree groupIn mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
s and free abelian groupFree abelian groupIn abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
s.
Discrete groups
Historically property (T) was established for discrete groups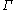 by embedding them as lattices in real or p-adic Lie groups with property (T). There are now several direct methods available.- The algebraic method of Shalom applies when
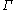= SLn(R) with R a ring and n≥ 3; the method relies on the fact that 
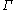can be boundedly generatedBoundedly generated groupIn mathematics, a group is called boundedly generated if it can be expressed as a finite product of cyclic subgroups. The property of bounded generation is also closely related with the congruence subgroup problem .- Definitions :...
, i.e. can be expressed as a finite product of easier subgroups, such as the elementary subgroups consisting of matrices differing from the identity matrix in one given off-diagonal position.
- The geometric method has its origins in ideas of Garland, Gromov and Pierre Pansu. Its simplest combinatorial version is due to Zuk: let
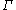be a discrete group generated by a finite subset S, closed under taking inverses and not containing the identity, and define a finite graphGraph (mathematics)In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
with vertices S and an edge between g and h whenever g−1 h lies in S. If this graph is connected and the smallest non-zero eigenvalue of its LaplacianLaplacian matrixIn the mathematical field of graph theory the Laplacian matrix, sometimes called admittance matrix or Kirchhoff matrix, is a matrix representation of a graph. Together with Kirchhoff's theorem it can be used to calculate the number of spanning trees for a given graph. The Laplacian matrix can be...
is greater than ½, then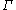
has property (T). A more general geometric version, due to Zuk and , states that if a discrete group 
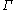acts properly discontinuousProperly discontinuousIn topology and related branches of mathematics, an action of a group G on a topological space X is called proper if the map from G×X to X×X taking to is proper, and is called properly discontinuous if in addition G is discrete...
ly and cocompactly on a contractible 2-dimensional simplicial complexSimplicial complexIn mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
with the same graph theoretic conditions placed on the link at each vertex, then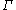
has property (T). Many new examples of hyperbolic groupHyperbolic groupIn group theory, a hyperbolic group, also known as a word hyperbolic group, Gromov hyperbolic group, negatively curved group is a finitely generated group equipped with a word metric satisfying certain properties characteristic of hyperbolic geometry. The notion of a hyperbolic group was introduced...
s with property (T) can be exhibited using this method.
Applications
- Grigory MargulisGrigory MargulisGregori Aleksandrovich Margulis is a Russian mathematician known for his far-reaching work on lattices in Lie groups, and the introduction of methods from ergodic theory into diophantine approximation. He was awarded a Fields Medal in 1978 and a Wolf Prize in Mathematics in 2005, becoming the...
used the fact that SLn(Z) (for n≥3) has property (T) to construct explicit families of expanding graphs, that is, graphs with the property that every subset has a uniformly large "boundary". This connection led to a number of recent studies giving an explicit estimate of Kazhdan constants, quantifying property (T) for a particular group and a generating set.
- Alain ConnesAlain ConnesAlain Connes is a French mathematician, currently Professor at the Collège de France, IHÉS, The Ohio State University and Vanderbilt University.-Work:...
used discrete groups with property (T) to find examples of type II1 factorsVon Neumann algebraIn mathematics, a von Neumann algebra or W*-algebra is a *-algebra of bounded operators on a Hilbert space that is closed in the weak operator topology and contains the identity operator. They were originally introduced by John von Neumann, motivated by his study of single operators, group...
with countable fundamental groupVon Neumann algebraIn mathematics, a von Neumann algebra or W*-algebra is a *-algebra of bounded operators on a Hilbert space that is closed in the weak operator topology and contains the identity operator. They were originally introduced by John von Neumann, motivated by his study of single operators, group...
, so in particular not the whole of the positive reals. Sorin Popa subsequently used relative property (T) for discrete groups to produce a type II1 factor with trivial fundamental group.
- Groups with property (T) lead to good mixingMixing (mathematics)In mathematics, mixing is an abstract concept originating from physics: the attempt to describe the irreversible thermodynamic process of mixing in the everyday world: mixing paint, mixing drinks, etc....
properties in ergodic theoryErgodic theoryErgodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
: again informally, a process which mixes slowly leaves some subsets almost invariant.
- Similarly, groups with property (T) can be used to construct finite sets of invertible matrices which can efficiently approximate any given invertible matrix, in the sense that every matrix can be approximated, to a high degree of accuracy, by a finite product of matrices in the list or their inverses, so that the number of matrices needed is proportional to the number of significant digits in the approximation.