
Free group
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
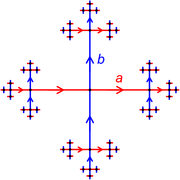
G is called free if there is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses (disregarding trivial variations such as st−1 = su−1ut−1). Apart from the existence of inverses no other relation exists between the generators of a free group.
A related but different notion is a free abelian group
Free abelian group
In abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
.
History
Free groups first arose in the study of hyperbolic geometryHyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
, as examples of Fuchsian group
Fuchsian group
In mathematics, a Fuchsian group is a discrete subgroup of PSL. The group PSL can be regarded as a group of isometries of the hyperbolic plane, or conformal transformations of the unit disc, or conformal transformations of the upper half plane, so a Fuchsian group can be regarded as a group acting...
s (discrete groups acting by isometries
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
on the hyperbolic plane
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
). In an 1882 paper, Walther von Dyck
Walther von Dyck
Walther Franz Anton von Dyck , born Dyck and later ennobled, was a German mathematician...
pointed out that these groups have the simplest possible presentations. The algebraic study of free groups was initiated by Jakob Nielsen
Jakob Nielsen (mathematician)
Jakob Nielsen was a Danish mathematician known for his work on automorphisms of surfaces. He was born in the village Mjels on the island of Als in North Schleswig, in modern day Denmark. His mother died when he was 3, and in 1900 he went to live with his aunt and was enrolled in the Realgymnasium...
in 1924, who gave them their name and established many of their basic properties. Max Dehn
Max Dehn
Max Dehn was a German American mathematician and a student of David Hilbert. He is most famous for his work in geometry, topology and geometric group theory...
realized the connection with topology, and obtained the first proof of the full Nielsen–Schreier theorem
Nielsen–Schreier theorem
In group theory, a branch of mathematics, the Nielsen–Schreier theorem is the statement that every subgroup of a free group is itself free. It is named after Jakob Nielsen and Otto Schreier.-Statement of the theorem:...
. Otto Schreier
Otto Schreier
Otto Schreier was an Austrian mathematician who made major contributions in combinatorial group theory and in the topology of Lie groups. He studied mathematics at the University of Vienna and obtained his doctorate in 1923, under the supervision of Philipp Furtwängler...
published an algebraic proof of this result in 1927, and Kurt Reidemeister
Kurt Reidemeister
Kurt Werner Friedrich Reidemeister was a mathematician born in Braunschweig , Germany.He received his doctorate in 1921 with a thesis in algebraic number theory at the University of Hamburg under the supervision of Erich Hecke. In 1923 he was appointed assistant professor at the University of Vienna...
included a comprehensive treatment of free groups in his 1932 book on combinatorial topology
Combinatorial topology
In mathematics, combinatorial topology was an older name for algebraic topology, dating from the time when topological invariants of spaces were regarded as derived from combinatorial decompositions such as simplicial complexes...
. Later on in the 1930s, Wilhelm Magnus
Wilhelm Magnus
Wilhelm Magnus was a mathematician. He made important contributions in combinatorial group theory, Lie algebras, mathematical physics, elliptic functions, and the study of tessellations....
discovered the connection between the lower central series of free groups and free Lie algebra
Free Lie algebra
In mathematics, a free Lie algebra, over a given field K, is a Lie algebra generated by a set X, without any imposed relations.-Definition:Given a set X, one can show that there exists a unique free Lie algebra L generated by X....
s.
Examples
The group (Z,+) of integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s is free; we can take S = {1}. A free group on a two-element set S occurs in the proof of the Banach–Tarski paradox
Banach–Tarski paradox
The Banach–Tarski paradox is a theorem in set theoretic geometry which states the following: Given a solid ball in 3-dimensional space, there exists a decomposition of the ball into a finite number of non-overlapping pieces , which can then be put back together in a different way to yield two...
and is described there.
On the other hand, any nontrivial finite group cannot be free, since the elements of a free generating set of a free group have infinite order.
In algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of a bouquet of k circles
Bouquet of circles
In mathematics, a rose is a topological space obtained by gluing together a collection of circles along a single point. The circles of the rose are called petals. Roses are important in algebraic topology, where they are closely related to free groups.- Definition :A rose is a wedge sum of circles...
(a set of k loops having only one point in common) is the free group on a set of k elements.
Construction
The free group FS with free generating set S can be constructed as follows. S is a set of symbols and we suppose for every s in S there is a corresponding "inverse" symbol, s−1, in a set S−1. Let T = S ∪ S−1, and define a word in S to be any written product of elements of T. That is, a word in S is an element of the monoidMonoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
generated by T. The empty word is the word with no symbols at all. For example, if S = {a, b, c}, then T = {a, a−1, b, b−1, c, c−1}, and
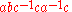
is a word in S. If an element of S lies immediately next to its inverse, the word may be simplified by omitting the s, s−1 pair:

A word that cannot be simplified further is called reduced. The free group FS is defined to be the group of all reduced words in S. The group operation in FS is concatenation
Concatenation
In computer programming, string concatenation is the operation of joining two character strings end-to-end. For example, the strings "snow" and "ball" may be concatenated to give "snowball"...
of words (followed by reduction if necessary). The identity is the empty word. A word is called cyclically reduced, if its first and last letter are not inverse to each other. Every word is conjugate
Inner automorphism
In abstract algebra an inner automorphism is a functionwhich, informally, involves a certain operation being applied, then another one performed, and then the initial operation being reversed...
to a cyclically reduced word, and the cyclically reduced conjugates of a cyclically reduced word are all cyclic permutations. For instance b−1abcb is not cyclically reduced, but is conjugate to abc, which is cyclically reduced. The only cyclically reduced conjugates of abc are abc, bca, and cab.
Universal property
The free group FS is the universal group generated by the set S. This can be formalized by the following universal propertyUniversal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
: given any function ƒ from S to a group G, there exists a unique homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
φ: FS → G making the following diagram
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
commute:
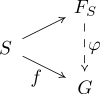
To see how this relates to the constructive definition, think of the mapping from S to FS as sending each symbol to a word consisting of that symbol. To construct φ for given ƒ, first note that φ sends the empty word to identity of G and it has to agree with ƒ on the elements of S. For the remaining words (consisting of more than one symbol) φ can be uniquely extended since it is a homomorphism, i.e., φ(ab) = φ(a) φ(b).
The above property characterizes free groups up to isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
, and is sometimes used as an alternative definition. It is known as the universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
of free groups, and the generating set S is called a basis for FS. The basis for a free group is not uniquely determined.
Being characterized by a universal property is the standard feature of free object
Free object
In mathematics, the idea of a free object is one of the basic concepts of abstract algebra. It is a part of universal algebra, in the sense that it relates to all types of algebraic structure . It also has a formulation in terms of category theory, although this is in yet more abstract terms....
s in universal algebra
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
. In the language of category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, the construction of the free group (similar to most constructions of free objects) is a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
from the category of sets
Category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
to the category of groups
Category of groups
In mathematics, the category Grp has the class of all groups for objects and group homomorphisms for morphisms. As such, it is a concrete category...
. This functor is left adjoint to the forgetful functor
Forgetful functor
In mathematics, in the area of category theory, a forgetful functor is a type of functor. The nomenclature is suggestive of such a functor's behaviour: given some object with structure as input, some or all of the object's structure or properties is 'forgotten' in the output...
from groups to sets.
Facts and theorems
Some properties of free groups follow readily from the definition:- Any group G is the homomorphic image of some free group F(S). Let S be a set of generatorsGenerating set of a groupIn abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
of G. The natural map f: F(S) → G is an epimorphismEpimorphismIn category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
, which proves the claim. Equivalently, G is isomorphic to a quotient groupQuotient groupIn mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
of some free group F(S). The kernel of f is a set of relations in the presentationPresentation of a groupIn mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
of G. If S can be chosen to be finite here, then G is called finitely generated. - If S has more than one element, then F(S) is not abelianAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
, and in fact the center of F(S) is trivial (that is, consists only of the identity element). - Two free groups F(S) and F(T) are isomorphic if and only if S and T have the same cardinality. This cardinality is called the rank of the free group F. Thus for every cardinal number k, there is, up toUp toIn mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
isomorphism, exactly one free group of rank k. - A free group of finite rank n > 1 has an exponentialExponential growthExponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...
growth rateGrowth rate (group theory)In group theory, the growth rate of a group with respect to a symmetric generating set describes the size of balls in the group. Every element in the group can be written as a product of generators, and the growth rate counts the number of elements that can be written as a product of length...
of order 2n − 1.
A few other related results are:
- The Nielsen–Schreier theoremNielsen–Schreier theoremIn group theory, a branch of mathematics, the Nielsen–Schreier theorem is the statement that every subgroup of a free group is itself free. It is named after Jakob Nielsen and Otto Schreier.-Statement of the theorem:...
: Any subgroupSubgroupIn group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of a free group is free. - A free group of rank k clearly has subgroups of every rank less than k. Less obviously, a free group of rank at least 2 has subgroups of all countableCountable setIn mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
ranks. - The commutator subgroupCommutator subgroupIn mathematics, more specifically in abstract algebra, the commutator subgroup or derived subgroup of a group is the subgroup generated by all the commutators of the group....
of a free group of rank k > 1 has infinite rank; for example for F(a,b), it is freely generated by the commutatorCommutatorIn mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
s [am, bn] for non-zero m and n. - The free group in two elements is SQ universal; the above follows as any SQ universal group has subgroups of all countable ranks.
- Any group that actsGroup actionIn algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on a tree, freely and preserving the orientation, is a free group of countable rank (given by 1 plus the Euler characteristicEuler characteristicIn mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
of the quotientGroup actionIn algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
graphGraph theoryIn mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
). - The Cayley graphCayley graphIn mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
of a free group of finite rank, with respect to a free generating set, is a tree on which the group acts freely, preserving the orientation. - The groupoidGroupoidIn mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:...
approach to these results, given in the work by P.J. Higgins below, is kind of extracted from an approach using covering spaces. It allows more powerful results, for example on Grushko's theorem, and a normal form for the fundamental groupoid of a graph of groups. In this approach there is considerable use of free groupoids on a directed graph. - Grushko's theorem has the consequence that if a subset B of a free group F on n elements generates F and has n elements, then B generates F freely.
Free abelian group
The free abelian group on a set S is defined via its universal property in the analogous way, with obvious modifications:Consider a pair (F, φ), where F is an abelian group and φ: S → F is a function. F is said to be the free abelian group on S with respect to φ if for any abelian group G and any function ψ: S → G, there exists a unique homomorphism f: F → G such that
- f(φ(s)) = ψ(s), for all s in S.
The free abelian group on S can be explicitly identified as the free group F(S) modulo the subgroup generated by its commutators, [F(S), F(S)], i.e.
its abelianisation. In other words, the free abelian group on S is the set of words that are distinguished only up to the order of letters. The rank of a free group can therefore also be defined as the rank of its abelianisation as a free abelian group.
Tarski's problems
Around 1945, Alfred TarskiAlfred Tarski
Alfred Tarski was a Polish logician and mathematician. Educated at the University of Warsaw and a member of the Lwow-Warsaw School of Logic and the Warsaw School of Mathematics and philosophy, he emigrated to the USA in 1939, and taught and carried out research in mathematics at the University of...
asked whether the free groups on two or more generators have the same first order theory
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, and whether this theory is decidable
Decidability (logic)
In logic, the term decidable refers to the decision problem, the question of the existence of an effective method for determining membership in a set of formulas. Logical systems such as propositional logic are decidable if membership in their set of logically valid formulas can be effectively...
. answered the first question by showing that any two nonabelian free groups have the same first order theory, and answered both questions, showing that this theory is decidable.
A similar unsolved (in 2011) question in free probability theory asks whether the von Neumann group algebras of any two non-abelian finitely generated free groups are isomorphic.
See also
- Generating set of a groupGenerating set of a groupIn abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
- Presentation of a groupPresentation of a groupIn mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
- Nielsen transformationNielsen transformationIn mathematics, especially in the area of abstract algebra known as combinatorial group theory, Nielsen transformations, named after Jakob Nielsen, are certain automorphisms of a free group which are a non-commutative analogue of row reduction and one of the main tools used in studying free groups,...
, a factorization of elements of the automorphism group of a free groupAutomorphism group of a free groupIn mathematical group theory, the automorphism group of a free group is a discrete group of automorphisms of a free group. The quotient by the inner automorphisms is the outer automorphism group of a free group, which is similar in some ways to the mapping class group of a surface.-Presentation:... - Free productFree productIn mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “most general” group having these properties...

