Geometric group theory
Encyclopedia
Geometric group theory is an area in mathematics
devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological
and geometric
properties of spaces on which these groups act
(that is, when the groups in question are realized as geometric symmetries or continuous transformations of some spaces).
Another important idea in geometric group theory is to consider finitely generated groups themselves as geometric objects. This is usually done by studying the Cayley graph
s of groups, which, in addition to the graph structure, are endowed with the structure of a metric space
, given by the so-called word metric.
Geometric group theory, as a distinct area, is relatively new, and has become a clearly identifiable branch of mathematics in late 1980s and early 1990s. Geometric group theory closely interacts with low-dimensional topology
, hyperbolic geometry
, algebraic topology
, computational group theory
and geometric analysis
. There are also substantial connections with complexity theory
, mathematical logic
, the study of Lie Group
s and their discrete subgroups, dynamical systems, probability theory
, K-theory
, and other areas of mathematics.
In the introduction to his book Topics in Geometric Group Theory, Pierre de la Harpe wrote: "One of my personal beliefs is that fascination with symmetries and groups is one way of coping with frustrations of life's limitations: we like to recognize symmetries which allow us to recognize more than what we can see. In this sense the study of geometric group theory is a part of culture, and reminds me of several things that Georges de Rham
practices on many occasions, such as teaching mathematics, reciting Mallarmé
, or greeting a friend" (page 3 in ).
that largely studied properties of discrete groups via analyzing group presentations
, that describe groups as quotients
of free group
s; this field was first systematically studied by Walther von Dyck
, student of Felix Klein
, in the early 1880s, while an early form is found in the 1856 Icosian Calculus
of William Rowan Hamilton
, where he studied the icosahedral symmetry
group via the edge graph of the dodecahedron. Currently combinatorial group theory as an area is largely subsumed by geometric group theory. Moreover, the term "geometric group theory" came to often include studying discrete groups using probabilistic, measure-theoretic, arithmetic, analytic and other approaches that lie outside of the traditional combinatorial group theory arsenal.
In the first half of the 20th century, pioneering work of Dehn
, Nielsen
, Reidemeister
and Schreier
, Whitehead
, van Kampen
, amongst others, introduced some topological and geometric ideas into the study of discrete groups. Other precursors of geometric group theory include small cancellation theory
and Bass–Serre theory.
Small cancellation theory was introduced by Martin Grindlinger in 1960s and further developed by Roger Lyndon
and Paul Schupp. It studies van Kampen diagram
s, corresponding to finite group presentations, via combinatorial curvature conditions and derives algebraic and algorithmic properties of groups from such analysis. Bass–Serre theory, introduced in the 1977 book of Serre, derives structural algebraic information about groups by studying group actions on simplicial trees
.
External precursors of geometric group theory include the study of lattices in Lie Groups, especially Mostow rigidity theorem
, the study of Kleinian group
s, and the progress achieved in low-dimensional topology and hyperbolic geometry in 1970s and early 1980s, spurred, in particular, by Thurston's
Geometrization program
.
The emergence of geometric group theory as a distinct area of mathematics is usually traced to late 1980s and early 1990s. It was spurred by the 1987 monograph of Gromov "Hyperbolic groups" that introduced the notion of a hyperbolic group
(also known as word-hyperbolic or Gromov-hyperbolic or negatively curved group), which captures the idea of a finitely generated group having large-scale negative curvature, and by his subsequent monograph Asymptotic Invariants of Inifinite Groups, that outlined Gromov's program of understanding discrete groups up to quasi-isometry. The work of Gromov had a transformative effect on the study of discrete groups and the phrase "geometric group theory" started appearing soon afterwards. (see, e.g.,).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and geometric
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
properties of spaces on which these groups act
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
(that is, when the groups in question are realized as geometric symmetries or continuous transformations of some spaces).
Another important idea in geometric group theory is to consider finitely generated groups themselves as geometric objects. This is usually done by studying the Cayley graph
Cayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
s of groups, which, in addition to the graph structure, are endowed with the structure of a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
, given by the so-called word metric.
Geometric group theory, as a distinct area, is relatively new, and has become a clearly identifiable branch of mathematics in late 1980s and early 1990s. Geometric group theory closely interacts with low-dimensional topology
Low-dimensional topology
In mathematics, low-dimensional topology is the branch of topology that studies manifolds of four or fewer dimensions. Representative topics are the structure theory of 3-manifolds and 4-manifolds, knot theory, and braid groups. It can be regarded as a part of geometric topology.A number of...
, hyperbolic geometry
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
, algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, computational group theory
Computational group theory
In mathematics, computational group theory is the study ofgroups by means of computers. It is concernedwith designing and analysing algorithms anddata structures to compute information about groups...
and geometric analysis
Geometric analysis
Geometric analysis is a mathematical discipline at the interface of differential geometry and differential equations. It includes both the use of geometrical methods in the study of partial differential equations , and the application of the theory of partial differential equations to geometry...
. There are also substantial connections with complexity theory
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, the study of Lie Group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s and their discrete subgroups, dynamical systems, probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, K-theory
K-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
, and other areas of mathematics.
In the introduction to his book Topics in Geometric Group Theory, Pierre de la Harpe wrote: "One of my personal beliefs is that fascination with symmetries and groups is one way of coping with frustrations of life's limitations: we like to recognize symmetries which allow us to recognize more than what we can see. In this sense the study of geometric group theory is a part of culture, and reminds me of several things that Georges de Rham
Georges de Rham
Georges de Rham was a Swiss mathematician, known for his contributions to differential topology.He studied at the University of Lausanne and then in Paris for a doctorate, becoming a lecturer in Lausanne in 1931; where he held positions until retirement in 1971; he held positions in Geneva in...
practices on many occasions, such as teaching mathematics, reciting Mallarmé
Stéphane Mallarmé
Stéphane Mallarmé , whose real name was Étienne Mallarmé, was a French poet and critic. He was a major French symbolist poet, and his work anticipated and inspired several revolutionary artistic schools of the early 20th century, such as Dadaism, Surrealism, and Futurism.-Biography:Stéphane...
, or greeting a friend" (page 3 in ).
Historical background
Geometric group theory grew out of combinatorial group theoryCombinatorial group theory
In mathematics, combinatorial group theory is the theory of free groups, and the concept of a presentation of a group by generators and relations...
that largely studied properties of discrete groups via analyzing group presentations
Presentation of a group
In mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
, that describe groups as quotients
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
of free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
s; this field was first systematically studied by Walther von Dyck
Walther von Dyck
Walther Franz Anton von Dyck , born Dyck and later ennobled, was a German mathematician...
, student of Felix Klein
Felix Klein
Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...
, in the early 1880s, while an early form is found in the 1856 Icosian Calculus
Icosian Calculus
The Icosian Calculus is a non-commutative algebraic structure discovered by the Irish mathematician William Rowan Hamilton in 1856.In modern terms, he gave a group presentation of the icosahedral rotation group by generators and relations....
of William Rowan Hamilton
William Rowan Hamilton
Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
, where he studied the icosahedral symmetry
Icosahedral symmetry
A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...
group via the edge graph of the dodecahedron. Currently combinatorial group theory as an area is largely subsumed by geometric group theory. Moreover, the term "geometric group theory" came to often include studying discrete groups using probabilistic, measure-theoretic, arithmetic, analytic and other approaches that lie outside of the traditional combinatorial group theory arsenal.
In the first half of the 20th century, pioneering work of Dehn
Max Dehn
Max Dehn was a German American mathematician and a student of David Hilbert. He is most famous for his work in geometry, topology and geometric group theory...
, Nielsen
Jakob Nielsen (mathematician)
Jakob Nielsen was a Danish mathematician known for his work on automorphisms of surfaces. He was born in the village Mjels on the island of Als in North Schleswig, in modern day Denmark. His mother died when he was 3, and in 1900 he went to live with his aunt and was enrolled in the Realgymnasium...
, Reidemeister
Kurt Reidemeister
Kurt Werner Friedrich Reidemeister was a mathematician born in Braunschweig , Germany.He received his doctorate in 1921 with a thesis in algebraic number theory at the University of Hamburg under the supervision of Erich Hecke. In 1923 he was appointed assistant professor at the University of Vienna...
and Schreier
Otto Schreier
Otto Schreier was an Austrian mathematician who made major contributions in combinatorial group theory and in the topology of Lie groups. He studied mathematics at the University of Vienna and obtained his doctorate in 1923, under the supervision of Philipp Furtwängler...
, Whitehead
J. H. C. Whitehead
John Henry Constantine Whitehead FRS , known as Henry, was a British mathematician and was one of the founders of homotopy theory. He was born in Chennai , in India, and died in Princeton, New Jersey, in 1960....
, van Kampen
Egbert van Kampen
Egbert Rudolf van Kampen was a mathematician. He made important contributions to topology, especially to the study of fundamental groups....
, amongst others, introduced some topological and geometric ideas into the study of discrete groups. Other precursors of geometric group theory include small cancellation theory
Small cancellation theory
In the mathematical subject of group theory, small cancellation theory studies groups given by group presentations satisfying small cancellation conditions, that is where defining relations have "small overlaps" with each other. It turns out that small cancellation conditions have substantial...
and Bass–Serre theory.
Small cancellation theory was introduced by Martin Grindlinger in 1960s and further developed by Roger Lyndon
Roger Lyndon
Roger Conant Lyndon was an American mathematician, for many years a professor at the University of Michigan. He is known for Lyndon words, the Curtis–Hedlund–Lyndon theorem, Craig–Lyndon interpolation and the Lyndon–Hochschild–Serre spectral sequence.-Biography:Lyndon was born on December 18, 1917...
and Paul Schupp. It studies van Kampen diagram
Van Kampen diagram
In the mathematical area of geometric group theory, a van Kampen diagram is a planar diagram used to represent the fact that a particular word in the generators of a group given by a group presentation represents the identity element in that group.-History:...
s, corresponding to finite group presentations, via combinatorial curvature conditions and derives algebraic and algorithmic properties of groups from such analysis. Bass–Serre theory, introduced in the 1977 book of Serre, derives structural algebraic information about groups by studying group actions on simplicial trees
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
.
External precursors of geometric group theory include the study of lattices in Lie Groups, especially Mostow rigidity theorem
Mostow rigidity theorem
In mathematics, Mostow's rigidity theorem, or strong rigidity theorem, or Mostow–Prasad rigidity theorem, essentially states that the geometry of a finite-volume hyperbolic manifold of dimension greater than two is determined by the fundamental group and hence unique...
, the study of Kleinian group
Kleinian group
In mathematics, a Kleinian group is a discrete subgroup of PSL. The group PSL of 2 by 2 complex matrices of determinant 1 modulo its center has several natural representations: as conformal transformations of the Riemann sphere, and as orientation-preserving isometries of 3-dimensional hyperbolic...
s, and the progress achieved in low-dimensional topology and hyperbolic geometry in 1970s and early 1980s, spurred, in particular, by Thurston's
William Thurston
William Paul Thurston is an American mathematician. He is a pioneer in the field of low-dimensional topology. In 1982, he was awarded the Fields Medal for his contributions to the study of 3-manifolds...
Geometrization program
Geometrization conjecture
Thurston's geometrization conjecture states that compact 3-manifolds can be decomposed canonically into submanifolds that have geometric structures. The geometrization conjecture is an analogue for 3-manifolds of the uniformization theorem for surfaces...
.
The emergence of geometric group theory as a distinct area of mathematics is usually traced to late 1980s and early 1990s. It was spurred by the 1987 monograph of Gromov "Hyperbolic groups" that introduced the notion of a hyperbolic group
Hyperbolic group
In group theory, a hyperbolic group, also known as a word hyperbolic group, Gromov hyperbolic group, negatively curved group is a finitely generated group equipped with a word metric satisfying certain properties characteristic of hyperbolic geometry. The notion of a hyperbolic group was introduced...
(also known as word-hyperbolic or Gromov-hyperbolic or negatively curved group), which captures the idea of a finitely generated group having large-scale negative curvature, and by his subsequent monograph Asymptotic Invariants of Inifinite Groups, that outlined Gromov's program of understanding discrete groups up to quasi-isometry. The work of Gromov had a transformative effect on the study of discrete groups and the phrase "geometric group theory" started appearing soon afterwards. (see, e.g.,).
Notable themes and developments in geometric group theory
Notable themes and developments in geometric group theory in 1990s and 2000s include:- Gromov's program to study quasi-isometric properties of groups.
- A particularly influential broad theme in the area is Gromov's program of classifying finitely generated groups according to their large scale geometry. Formally, this means classifying finitely generated groups with their word metric up to quasi-isometry. This program involves:
- The study of properties that are invariant under quasi-isometry. Examples of such properties of finitely generated groups include: the growth rateGrowth rate (group theory)In group theory, the growth rate of a group with respect to a symmetric generating set describes the size of balls in the group. Every element in the group can be written as a product of generators, and the growth rate counts the number of elements that can be written as a product of length...
of a finitely generated group; the isoperimetric function or Dehn functionVan Kampen diagramIn the mathematical area of geometric group theory, a van Kampen diagram is a planar diagram used to represent the fact that a particular word in the generators of a group given by a group presentation represents the identity element in that group.-History:...
of a finitely presented group; the number of ends of a group; hyperbolicity of a groupHyperbolic groupIn group theory, a hyperbolic group, also known as a word hyperbolic group, Gromov hyperbolic group, negatively curved group is a finitely generated group equipped with a word metric satisfying certain properties characteristic of hyperbolic geometry. The notion of a hyperbolic group was introduced...
; the homeomorphism type of the boundary of a hyperbolic group; asymptotic coneUltralimitIn mathematics, an ultralimit is a geometric construction that assigns to a sequence of metric spaces Xn a limiting metric space. The notion of an ultralimit captures the limiting behavior of finite configurations in the spaces Xn and uses an ultrafilter to avoid the process of repeatedly passing...
s of finitely generated groups (see, e.g.,); amenability of a finitely generated group; being virtually abelianAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
(that is, having an abelian subgroup of finite index); being virtually nilpotentNilpotent groupIn mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
; being virtually freeFree groupIn mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
; being finitely presentable; being a finitely presentable group with solvable Word ProblemWord problem for groupsIn mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a finitely generated group G is the algorithmic problem of deciding whether two words in the generators represent the same element...
; and others. - Theorems which use quasi-isometry invariants to prove algebraic results about groups, for example: Gromov's polynomial growth theoremGromov's theorem on groups of polynomial growthIn geometric group theory, Gromov's theorem on groups of polynomial growth, named for Mikhail Gromov, characterizes finitely generated groups of polynomial growth, as those groups which have nilpotent subgroups of finite index....
; Stallings' ends theorem; Mostow rigidity theoremMostow rigidity theoremIn mathematics, Mostow's rigidity theorem, or strong rigidity theorem, or Mostow–Prasad rigidity theorem, essentially states that the geometry of a finite-volume hyperbolic manifold of dimension greater than two is determined by the fundamental group and hence unique...
. - Quasi-isometric rigidity theorems, in which one classifies algebraically all groups that are quasi-isometric to some given group or metric space. This direction was initiated by the work of SchwartzRichard SchwartzRichard Evan Schwartz is an American mathematician notable for his contributions to geometric group theory and to an area of mathematics known as billiards...
on quasi-isometric rigidity of rank-one lattices and the work of Farb and Mosher on quasi-isometric rigidity of Baumslag-Solitar groups.- The theory of word-hyperbolicHyperbolic groupIn group theory, a hyperbolic group, also known as a word hyperbolic group, Gromov hyperbolic group, negatively curved group is a finitely generated group equipped with a word metric satisfying certain properties characteristic of hyperbolic geometry. The notion of a hyperbolic group was introduced...
and relatively hyperbolicRelatively hyperbolic groupIn mathematics, the concept of a relatively hyperbolic group is an important generalization of the geometric group theory concept of a hyperbolic group...
groups. A particularly important development here is the work of SelaZlil SelaZlil Sela is an Israeli mathematician working in the area of geometric group theory.He is a Professor of Mathematics at the Hebrew University of Jerusalem...
in 1990s resulting in the solution of the isomorphism problem for word-hyperbolic groups. The notion of a relatively hyperbolic groups was originally introduced by Gromov in 1987 and refined by Farb and BowditchBrian BowditchBrian Hayward Bowditch is a British mathematician known for his contributions to geometry and topology, particularly in the areas of geometric group theory and low-dimensional topology. He is also known for solving the angel problem...
, in the 1990s. The study of relatively hyperbolic groups gained prominence in 2000s. - Interactions with mathematical logic and the study of first-order theory of free groups. Particularly important progress occurred on the famous Tarski conjectures, due to the work of Sela as well as of Kharlampovich and Myasnikov. The study of limit groups and introduction of the language and machinery of non-commutative algebraic geometry gained prominence.
- Interactions with computer science, complexity theory and the theory of formal languages. This theme is exemplified by the development of the theory of automatic groupAutomatic groupIn mathematics, an automatic group is a finitely generated group equipped with several finite-state automata. These automata can tell if a given word representation of a group element is in a "canonical form" and can tell if two elements given in canonical words differ by a generator.More...
s, a notion that imposes certain geometric and language theoretic conditions on the multiplication operation in a finitely generate group. - The study of isoperimetric inequalities, Dehn functions and their generalizations for finitely presented group. This includes, in particular, the work of Birget, Ol'shanskii, RipsEliyahu RipsEliyahu Rips, also Ilya Rips is a Latvian-born Israeli mathematician known for his research in geometric group theory. He became known to the general public following his coauthoring a paper on the Torah Code....
and Sapir essentially characterizing the possible Dehn functions of finitely presented groups, as well as results providing explicit constructions of groups with fractional Dehn functions. - Development of the theory of JSJ-decompositions for finitely generated and finitely presented groups.
- Connections with geometric analysisGeometric analysisGeometric analysis is a mathematical discipline at the interface of differential geometry and differential equations. It includes both the use of geometrical methods in the study of partial differential equations , and the application of the theory of partial differential equations to geometry...
, the study of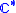
-algebras associated with discrete groups and of the theory of free probability. This theme is represented, in particular, by considerable progress on the Novikov conjectureNovikov conjectureThe Novikov conjecture is one of the most important unsolved problems in topology. It is named for Sergei Novikov who originally posed the conjecture in 1965....
and the Baum-Connes conjecture and the development and study of related group-theoretic notions such as topological amenability, asymptotic dimension, uniform embeddability into Hilbert spaces, rapid decay property, and so on (see, for example,). - Interactions with the theory of quasiconformal analysis on metric spaces, particularly in relation to Cannon's Conjecture about characterization of hyperbolic groups with boundary homeomorphic to the 2-sphere.
- Interactions with topological dynamicsTopological dynamicsIn mathematics, topological dynamics is a branch of the theory of dynamical systems in which qualitative, asymptotic properties of dynamical systems are studied from the viewpoint of general topology.- Scope :...
in the contexts of studying actions of discrete groups on various compact spaces and group compactifications, particularly convergence group methods - Development of the theory of group actions on
-treesReal treeA real tree, or an \mathbb R-tree, is a metric space such thatfor any x, y in M there is a unique arc from x to y and this arc is a geodesic segment. Here by an arc from x to y we mean the image in M of a topological embedding f from an interval [a,b] to M such that f=x and f=y...
(particularly the Rips machine), and its applications. - The study of group actions on CAT(0) spaces and CAT(0) cubical complexes, motivated by ideas from Alexandrov geometry.
- Interactions with low-dimensional topology and hyperbolic geometry, particularly the study of 3-manifold groups (see, e.g.,), mapping class groupMapping class groupIn mathematics, in the sub-field of geometric topology, the mapping class groupis an important algebraic invariant of a topological space. Briefly, the mapping class group is a discrete group of 'symmetries' of the space.-Motivation:...
s of surfaces, braid groupBraid groupIn mathematics, the braid group on n strands, denoted by Bn, is a group which has an intuitive geometrical representation, and in a sense generalizes the symmetric group Sn. Here, n is a natural number; if n > 1, then Bn is an infinite group...
s and Kleinian groupKleinian groupIn mathematics, a Kleinian group is a discrete subgroup of PSL. The group PSL of 2 by 2 complex matrices of determinant 1 modulo its center has several natural representations: as conformal transformations of the Riemann sphere, and as orientation-preserving isometries of 3-dimensional hyperbolic...
s. - Introduction of probabilistic methods to study algebraic properties of "random" group theoretic objects (groups, group elements, subgroups, etc.). A particularly important development here is the work of Gromov who used probabilistic methods to prove the existence of a finitely generated group that is not uniformly embeddable into a Hilbert space. Other notable developments include introduction and study of the notion of generic-case complexityGeneric-case complexityGeneric-case complexity is a subfield of computational complexity theory that studies the complexity of computational problems on "most inputs".Generic-case complexity is a way of measuring the complexity of a computational problem by neglecting a small set of...
for group-theoretic and other mathematical algorithms and algebraic rigidity results for generic groups. - The study of automata groups and iterated monodromy groupIterated monodromy groupIn geometric group theory and dynamical systems the iterated monodromy group of a covering map is a group describing the monodromy action of the fundamental group on all iterations of the covering...
s as groups of automorphisms of infinite rooted trees. In particular, Grigorchuk's groups of intermediate growth, and their generalizations, appear in this context. - The study of measure-theoretic properties of group actions on measure spaces, particularly introduction and development of the notions of measure equivalence and orbit equivalence, as well as measure-theoretic generalizations of Mostow rigidity.
- The study of unitary representations of discrete groups and Kazhdan's property (T)Kazhdan's property (T)In mathematics, a locally compact topological group G has property if the trivial representation is an isolated point in its unitary dual equipped with the Fell topology. Informally, this means that if G acts unitarily on a Hilbert space and has "almost invariant vectors", then it has a nonzero...
- The study of Out(Fn) (the outer automorphism groupOuter automorphism groupIn mathematics, the outer automorphism group of a group Gis the quotient Aut / Inn, where Aut is the automorphism group of G and Inn is the subgroup consisting of inner automorphisms. The outer automorphism group is usually denoted Out...
of a free groupFree groupIn mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
of rank n) and of individual automorphisms of free groups. Introduction and the study of Culler-Vogtmann's outer space and of the theory of train trackTrain trackIn the mathematical area of topology, a train track is a family of curves embedded on a surface, meeting the following conditions:#The curves meet at a finite set of vertices called switches....
s for free group automorphisms played a particularly prominent role here. - Development of Bass–Serre theory, particularly various accessibility results and the theory of tree lattices. Generalizations of Bass–Serre theory such as the theory of complexes of groups.
- The study of random walkRandom walkA random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
s on groups and related boundary theory, particularly the notion of Poisson boundary (see, e.g.,). The study of amenabilityAmenable groupIn mathematics, an amenable group is a locally compact topological group G carrying a kind of averaging operation on bounded functions that is invariant under translation by group elements...
and of groups whose amenability status is still unknown. - Interactions with finite group theory, particularly progress in the study of subgroup growthSubgroup growthIn mathematics, subgroup growth is a branch of group theory, dealing with quantitative questions about subgroups of a given group.Let G be a finitely generated group. Then, for each integer n define n to be the number of subgroups U of index n in G...
. - Studying subgroups and lattices in linear groups, such as
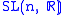, and of other Lie Groups, via geometric methods (e.g. buildings), algebro-geometricAlgebraic geometryAlgebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
tools (e.g. algebraic groupAlgebraic groupIn algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
s and representation varieties), analytic methods (e.g. unitary representations on Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s) and arithmetic methods. - Group cohomologyGroup cohomologyIn abstract algebra, homological algebra, algebraic topology and algebraic number theory, as well as in applications to group theory proper, group cohomology is a way to study groups using a sequence of functors H n. The study of fixed points of groups acting on modules and quotient modules...
, using algebraic and topological methods, particularly involving interaction with algebraic topologyAlgebraic topologyAlgebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
and the use of morse-theoreticMorse theoryIn differential topology, the techniques of Morse theory give a very direct way of analyzing the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a differentiable function on a manifold will, in a typical case, reflect...
ideas in the combinatorial context; large-scale, or coarse (e.g. see ) homological and cohomological methods. - Progress on traditional combinatorial group theory topics, such as the Burnside problem, the study of Coxeter groupCoxeter groupIn mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
s and Artin groups, and so on (the methods used to study these questions currently are often geometric and topological).
- The theory of word-hyperbolic
- The study of properties that are invariant under quasi-isometry. Examples of such properties of finitely generated groups include: the growth rate
See also
- The Ping-pong lemmaPing-pong lemmaIn mathematics, the ping-pong lemma, or table-tennis lemma, is any of several mathematical statements that ensure that several elements in a group acting on a set freely generate a free subgroup of that group.-History:...
, a useful way to exhibit a group as a free product - Amenable groupAmenable groupIn mathematics, an amenable group is a locally compact topological group G carrying a kind of averaging operation on bounded functions that is invariant under translation by group elements...
- Nielsen transformationNielsen transformationIn mathematics, especially in the area of abstract algebra known as combinatorial group theory, Nielsen transformations, named after Jakob Nielsen, are certain automorphisms of a free group which are a non-commutative analogue of row reduction and one of the main tools used in studying free groups,...
- Tietze transformation
Books and monographs on or closely related to geometric group theory
- B. H. Bowditch. A course on geometric group theory. MSJ Memoirs, 16. Mathematical Society of Japan, Tokyo, 2006. ISBN 4-931469-35-3
- M. R. Bridson and A. Haefliger, Metric spaces of non-positive curvature. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 319. Springer-Verlag, Berlin, 1999. ISBN 3-540-64324-9
- Michel Coornaert, Thomas Delzant and Athanase Papadopoulos, "Géométrie et théorie des groupes : les groupes hyperboliques de Gromov", Lecture Notes in Mathematics, vol. 1441, Springer-Verlag, Berlin, 1990, x+165 pp. MR 92f:57003, ISBN 3-540-52977-2
- Michel Coornaert and Athanase Papadopoulos, Symbolic dynamics and hyperbolic groups. Lecture Notes in Mathematics. 1539. Springer-Verlag, Berlin, 1993, viii+138 pp. ISBN 3-540-56499-3
- P. de la Harpe, Topics in geometric group theory. Chicago Lectures in Mathematics. University of Chicago Press, Chicago, IL, 2000. ISBN 0-226-31719-6
- D. B. A. Epstein, J. W. Cannon, D. Holt, S. Levy, M. Paterson, W. Thurston. Word processing in groups. Jones and Bartlett Publishers, Boston, MA, 1992. ISBN 0-86720-244-0
- M. Gromov, Hyperbolic Groups, in "Essays in Group Theory" (G. M. Gersten, ed.), MSRI Publ. 8, 1987, pp. 75–263. ISBN 0-387-96618-8
- M. Gromov, Asymptotic invariants of infinite groups, in "Geometric Group Theory", Vol. 2 (Sussex, 1991), London Mathematical Society Lecture Note Series, 182, Cambridge University Press, Cambridge, 1993, pp. 1–295
- M. Kapovich, Hyperbolic manifolds and discrete groups. Progress in Mathematics, 183. Birkhäuser Boston, Inc., Boston, MA, 2001
- R. LyndonRoger LyndonRoger Conant Lyndon was an American mathematician, for many years a professor at the University of Michigan. He is known for Lyndon words, the Curtis–Hedlund–Lyndon theorem, Craig–Lyndon interpolation and the Lyndon–Hochschild–Serre spectral sequence.-Biography:Lyndon was born on December 18, 1917...
and P. Schupp, Combinatorial Group Theory, Springer-Verlag, Berlin, 1977. Reprinted in the "Classics in mathematics" series, 2000. ISBN 3-540-41158-5 - A. Yu. Ol'shanskii, Geometry of defining relations in groups. Translated from the 1989 Russian original by Yu. A. Bakhturin. Mathematics and its Applications (Soviet Series), 70. Kluwer Academic Publishers Group, Dordrecht, 1991
- J. Roe, Lectures on coarse geometry. University Lecture Series, 31. American Mathematical Society, Providence, RI, 2003. ISBN 0-8218-3332-4