
Semimartingale
Encyclopedia
In probability theory, a real valued process
X is called a semimartingale if it can be decomposed as the sum of a local martingale
and an adapted finite-variation process.
Semimartingales are "good integrators", forming the largest class of processes with respect to which the Itō integral can be defined.
The class of semimartingales is quite large (including, for example, all continuously differentiable processes, Brownian motion
and Poisson process
es). Submartingales and supermartingales together represent a subset of the semimartingales.

where M is a local martingale
and A is a càdlàg
adapted process
of locally bounded variation
.
An Rn-valued process X = (X1,…,Xn) is a semimartingale if each of its components Xi is a semimartingale.
es are defined to be linear combinations of processes of the form Ht = A1{t > T} for stopping times T and FT -measurable random variables A. The integral H · X for any such simple predictable process H and real valued process X is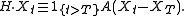
This is extended to all simple predictable processes by the linearity of H · X in H.
A real valued process X is a semimartingale if it is càdlàg, adapted, and for every t ≥ 0,

is bounded in probability. The Bichteler-Dellacherie Theorem states that these two definitions are equivalent .
Although most continuous and adapted processes studied in the literature are semimartingales, this is not always the case.
For example, if X is an Itō process satisfying the stochastic differential equation dXt = σt dWt + bt dt, then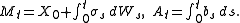
Every special semimartingale is a semimartingale. Conversely, a semimartingale is a special semimartingale if and only if the process Xt* ≡ sups ≤ t |Xs| is locally integrable .
For example, every continuous semimartingale is a special semimartingale, in which case M and A are both continuous processes.
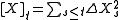 .
.
Every adapted finite variation process is a purely discontinuous semimartingale. A continuous process is a purely discontinuous semimartingale if and only if it is an adapted finite variation process.
Then, every semimartingale has the unique decomposition X = M + A where M is a continuous local martingale and A is a purely discontinuous semimartingale starting at zero. The local martingale M - M0 is called the continuous martingale part of X, and written as Xc .
In particular, if X is continuous, then M and A are continuous.
. A process X on the manifold M is a semimartingale if f(X) is a semimartingale for every smooth function f from M to R. Stochastic calculus for semimartingales on general manifolds requires the use of the Stratonovich integral
.
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
X is called a semimartingale if it can be decomposed as the sum of a local martingale
Local martingale
In mathematics, a local martingale is a type of stochastic process, satisfying the localized version of the martingale property. Every martingale is a local martingale; every bounded local martingale is a martingale; however, in general a local martingale is not a martingale, because its...
and an adapted finite-variation process.
Semimartingales are "good integrators", forming the largest class of processes with respect to which the Itō integral can be defined.
The class of semimartingales is quite large (including, for example, all continuously differentiable processes, Brownian motion
Wiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
and Poisson process
Poisson process
A Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
es). Submartingales and supermartingales together represent a subset of the semimartingales.
Definition
A real valued process X defined on the filtered probability space (Ω,F,(Ft)t ≥ 0,P) is called a semimartingale if it can be decomposed as
where M is a local martingale
Local martingale
In mathematics, a local martingale is a type of stochastic process, satisfying the localized version of the martingale property. Every martingale is a local martingale; every bounded local martingale is a martingale; however, in general a local martingale is not a martingale, because its...
and A is a càdlàg
Càdlàg
In mathematics, a càdlàg , RCLL , or corlol function is a function defined on the real numbers that is everywhere right-continuous and has left limits everywhere...
adapted process
Adapted process
In the study of stochastic processes, an adapted process is one that cannot "see into the future". An informal interpretation is that X is adapted if and only if, for every realisation and every n, Xn is known at time n...
of locally bounded variation
Bounded variation
In mathematical analysis, a function of bounded variation, also known as a BV function, is a real-valued function whose total variation is bounded : the graph of a function having this property is well behaved in a precise sense...
.
An Rn-valued process X = (X1,…,Xn) is a semimartingale if each of its components Xi is a semimartingale.
Alternative definition
First, the simple predictable processPredictable process
In stochastic analysis, a part of the mathematical theory of probability, a predictable process is a stochastic process which the value is knowable at a prior time...
es are defined to be linear combinations of processes of the form Ht = A1{t > T} for stopping times T and FT -measurable random variables A. The integral H · X for any such simple predictable process H and real valued process X is
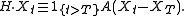
This is extended to all simple predictable processes by the linearity of H · X in H.
A real valued process X is a semimartingale if it is càdlàg, adapted, and for every t ≥ 0,

is bounded in probability. The Bichteler-Dellacherie Theorem states that these two definitions are equivalent .
Examples
- Adapted and continuously differentiable processes are finite variation processes, and hence are semimartingales.
- Brownian motionWiener processIn mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
is a semimartingale. - All càdlàg martingalesMartingale (probability theory)In probability theory, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence of random variables for which, at a particular time in the realized sequence, the expectation of the next value in the...
, submartingales and supermartingales are semimartingales. - Itō processes, which satisfy a stochastic differential equation of the form dX = σdW + μdt are semimartingales. Here, W is a Brownian motion and σ, μ are adapted processes.
- Every Lévy processLévy processIn probability theory, a Lévy process, named after the French mathematician Paul Lévy, is any continuous-time stochastic process that starts at 0, admits càdlàg modification and has "stationary independent increments" — this phrase will be explained below...
is a semimartingale.
Although most continuous and adapted processes studied in the literature are semimartingales, this is not always the case.
- Fractional Brownian motion with Hurst parameter H ≠ 1/2 is not a semimartingale.
Properties
- The semimartingales form the largest class of processes for which the Itō integralIto calculusItō calculus, named after Kiyoshi Itō, extends the methods of calculus to stochastic processes such as Brownian motion . It has important applications in mathematical finance and stochastic differential equations....
can be defined. - Linear combinations of semimartingales are semimartingales.
- Products of semimartingales are semimartingales, which is a consequence of the integration by parts formula for the Itō integralStochastic calculusStochastic calculus is a branch of mathematics that operates on stochastic processes. It allows a consistent theory of integration to be defined for integrals of stochastic processes with respect to stochastic processes...
. - The quadratic variationQuadratic variationIn mathematics, quadratic variation is used in the analysis of stochastic processes such as Brownian motion and martingales. Quadratic variation is just one kind of variation of a process.- Definition :...
exists for every semimartingale. - The class of semimartingales is closed under optional stoppingStopped processIn mathematics, a stopped process is a stochastic process that is forced to assume the same value after a prescribed time.-Definition:Let* be a probability space;...
, localization, change of time and absolutely continuous change of measure. - If X is an Rm valued semimartingale and f is a twice continuously differentiable function from Rm to Rn, then f(X) is a semimartingale. This is a consequence of Itō's lemmaIto's lemmaIn mathematics, Itō's lemma is used in Itō stochastic calculus to find the differential of a function of a particular type of stochastic process. It is named after its discoverer, Kiyoshi Itō...
. - The property of being a semimartingale is preserved under shrinking the filtration. More precisely, if X is a semimartingale with respect to the filtration Ft, and is adapted with respect to the subfiltration Gt, then X is a Gt-semimartingale.
- (Jacod's Countable Expansion) The property of being a semimartingale is preserved under enlarging the filtration by a countable set of disjoint sets. Suppose that Ft is a filtration, and Gt is the filtration generated by Ft and a countable set of disjoint measurable sets. Then, every Ft-semimartingale is also a Gt-semimartingale.
Semimartingale decompositions
By definition, every semimartingale is a sum of a local martingale and a finite variation process. However, this decomposition is not unique.Continuous semimartingales
A continuous semimartingale uniquely decomposes as X = M + A where M is a continuous local martingale and A is a continuous finite variation process starting at zero.For example, if X is an Itō process satisfying the stochastic differential equation dXt = σt dWt + bt dt, then
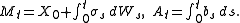
Special semimartingales
A special semimartingale is a real valued process X with the decomposition X = M + A, where M is a local martingale and A is a predictable finite variation process starting at zero. If this decomposition exists, then it is unique up to a P-null set.Every special semimartingale is a semimartingale. Conversely, a semimartingale is a special semimartingale if and only if the process Xt* ≡ sups ≤ t |Xs| is locally integrable .
For example, every continuous semimartingale is a special semimartingale, in which case M and A are both continuous processes.
Purely discontinuous semimartingales
A semimartingale is called purely discontinuous if its quadratic variation [X] is a pure jump process,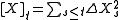 .
.Every adapted finite variation process is a purely discontinuous semimartingale. A continuous process is a purely discontinuous semimartingale if and only if it is an adapted finite variation process.
Then, every semimartingale has the unique decomposition X = M + A where M is a continuous local martingale and A is a purely discontinuous semimartingale starting at zero. The local martingale M - M0 is called the continuous martingale part of X, and written as Xc .
In particular, if X is continuous, then M and A are continuous.
Semimartingales on a manifold
The concept of semimartingales, and the associated theory of stochastic calculus, extends to processes taking values in a differentiable manifoldDifferentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
. A process X on the manifold M is a semimartingale if f(X) is a semimartingale for every smooth function f from M to R. Stochastic calculus for semimartingales on general manifolds requires the use of the Stratonovich integral
Stratonovich integral
In stochastic processes, the Stratonovich integral is a stochastic integral, the most common alternative to the Itō integral...
.

