Holomorphic functional calculus
Encyclopedia
In mathematics
, holomorphic functional calculus is functional calculus
with holomorphic function
s. That is to say, given a holomorphic function ƒ of a complex
argument z and an operator T, the aim is to construct an operator
which in a sense extends the function ƒ from complex argument to operator argument.
This article will discuss the case where T is a bounded linear operator on some Banach space
. In particular, T can be a square matrix with complex entries, a case which will be used to illustrate functional calculus and provide some heuristic insights for the assumptions involved in the general construction.
If a given function ƒ is of certain special type, there are natural ways of defining ƒ(T). For instance, if
is a complex polynomial
, one can simply substitute T for z and define
where T0 = I, the identity matrix
. This is the polynomial functional calculus. It is a homomorphism from the ring of polynomials to the ring of n × n matrices.
Extending slightly from the polynomials, if
is holomorphic everywhere, i.e. an entire function
, with MacLaurin series
mimicking the polynomial case suggests we define
Since the MacLaurin series converges everywhere, the above series will converge, in a chosen operator norm
. An example of this is the exponential
of a matrix. Replacing z by T in the MacLaurin series of f(z) = ez gives
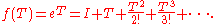
The requirement that the MacLaurin series of ƒ converges everywhere can be relaxed somewhat. From above it is evident that all that is really needed is the radius of convergence of the MacLaurin series be greater than
the operator norm of T. This enlarges somewhat the family of f for which ƒ(T) can be defined using the above approach. However it is not quite satisfactory. For instance, it is a fact from matrix theory that every non-singular T has a logarithm S in the sense that
It is desirable to have a functional calculus that allows one to define, for a non-singular T,
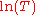
such that it coincides with S. This can not be done via power series. For example, the logarithmic series
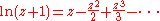
converges only on the open unit disk. Substituting T for z in the series fails to give a well-defined ln (T + I) for any invertible T + I with
Thus a more general functional calculus is needed.
of T. For example, the spectral theorem for normal matrices states every normal matrix is unitarily diagonalizable. There leads to a definition of ƒ(T) when T is normal. One encounters difficulties if ƒ(λ) is not defined for some eigenvalue λ of T.
Other indications also reinforce the idea that ƒ(T) can be defined only if ƒ is defined on the spectrum of T. If T is not invertible, then 0 is an eigenvalue. Since the natural logarithm is undefined at 0, one would expect that ln(T) can not be defined naturally. This is indeed the case. As another example, for
the reasonable way of calculating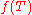
would seem to be
However, this expression is not defined if the inverses on the right-hand side do not exist, that is, if either 2 or 5 are eigenvalues of T.
For a given matrix T, the eigenvalues of T dictates to what extent ƒ(T) can be defined; ƒ(λ) must be defined for all eigenvalue λ of T. For a general bounded operator this condition translates to "ƒ must be defined on the spectrum
of T". This assumption turns out to be an enabling condition such that the functional calculus map
has certain desirable properties.
Let X be a complex Banach space, and L(X) denote the family of bounded operators on X.
Recall the Cauchy integral formula from classical function theory. Let
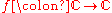
be holomorphic on some open
subset D in the complex plane, and
be a rectifiable Jordan curve in D, that is, a closed curve of finite length without self-intersections. Cauchy's integral formula states
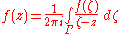
for any z lying in the inside of Γ, i.e. the winding number
of Γ about z is 1.
The idea is to extend this formula to functions taking values in the Banach space L(X). Cauchy's integral formula suggests the following definition (purely formal, for now):
where (ζ - T)-1 is the resolvent of T at ζ.
Assuming this Banach space-valued integral is appropriately defined, this proposed functional calculus implies the following necessary conditions:
The full definition of the functional calculus is as follows: For T ∈ L(X), define
where f is a holomorphic function defined on an open set
D in the complex plane which contains σ(T), and
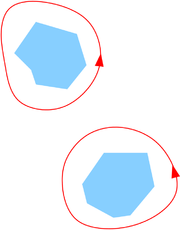
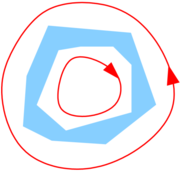
is a collection of Jordan curves in D such that σ(T) lies in the inside of Γ, and each γi is oriented in the positive sense.
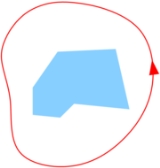
The open set D may vary with ƒ and need not be connected, as shown by the figures on the right.
The following subsections make precise the notions invoked in the definition and show ƒ(T) is indeed well defined under given assumptions.
For a continuous function g defined in an open neighborhood of Γ and taking values in L(X), the contour integral ∫Γg is defined in the same way as for the scalar case. One can parametrize each γi ∈ Γ by a real interval [a, b], and the integral is the limit of the Riemann sums obtained from ever-finer partitions of [a, b]. The Riemann sums converge in the uniform operator topology
. We define
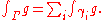
In the definition of the functional calculus, ƒ is assumed to be holomorphic in an open neighborhood of Γ. It will be shown below that the resolvent mapping is holomorphic on the resolvent set. Therefore the integral
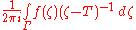
makes sense.
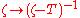
is called the resolvent mapping of T. It is defined on the complement of σ(T), called the resolvent set of T and will be denoted by ρ(T).
Much of classical function theory depends on the properties of the integral
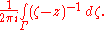
The holomorphic functional calculus is similar in that the resolvent mapping plays a crucial role in obtaining properties one requires from a nice functional calculus. This subsection outlines properties of the resolvent map that are essential in this context.
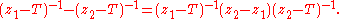
Therefore
This equation is called the first resolvent formula. The formula shows (z1 − T)−1 and (z2 − T)−1 commute, which hints at the fact that the image of the functional calculus will be a commutative algebra. Letting z2 → z1 shows the resolvent map is (complex-) differentiable at each z1 ∈ ρ(T); so the integral in the expression of functional calculus converges in L(X).
suggests we consider
for (z2 − T)−1. The above series converges in L(X), which implies the existence of (z2 − T)−1, if
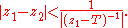
Therefore the resolvent set ρ(T) is open and the power series expression on an open disk centered at z1 ∈ ρ(T) shows the resolvent map is holomorphic on ρ(T).
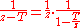
leads one to consider
This series, the Neumann series, converges to (z − T)−1 if
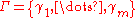
such that σ(T) is in the inside of Γ and the complement of D is contained in the outside of Γ. Hence, for the definition of the functional calculus, indeed a suitable family of Jordan curves can be found for each f that is holomorphic on some D.
Theorem Let G ⊂ C be an open set and Γ ⊂ G. If g: C → C be holomorphic on G, and for all a in the complement of G, n(Γ, a) = 0, then the contour integral ∫Γ g = 0.
We will need the vector-valued analog of this result when g takes values in L(X). To this end, let g: G → L(X) be holomorphic, with the same assumptions on Γ. The idea is use the dual space
L(X)* of L(X), and pass to Cauchy's theorem for the scalar case.
Consider the integral ∫Γ g ∈ L(X). If we can show, for all φ ∈ L(X)*, φ (∫Γ g) = 0, then the claim, that ∫Γ g = 0, follows. By boundedness of φ and the fact that the integral converges in norm,
But g is holomorphic implies the composition φ(g): G ⊂ C → C is holomorphic. So by Cauchy's theorem
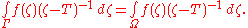
Let Ω be obtained from Ω by reversing the orientation of each ωj, then
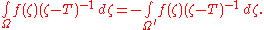
Consider the union of the two collections Γ ∪ Ω' . Both Γ ∪ Ω' and σ(T) are compact. So there is some open set U containing Γ ∪ Ω' such that σ(T) lies in the complement of U. Any a in the complement of U has winding number n(Γ ∪ Ω, a) = 0 and the function
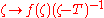
is holomorphic on U. So the vector-valued version of Cauchy's theorem gives
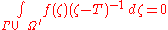
i.e.
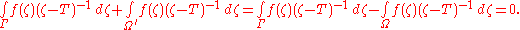
Hence the functional calculus is well-defined.
Consequently, if f1 and f2 are two holomorphic functions defined on corresponding neighborhoods D1 and D2 of σ(T) and they are equal on an open set containing σ(T), then f1(T) = f2(T). Moreover, even though the D1 may not be D2, the operator (f1 + f2) (T) is well-defined. Same holds for the definition of (f1·f2)(T).
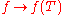
follows from the convergence of the integral and that linear operations on a Banach space are continuous.
We recover the polynomial functional calculus when f(z) = ∑0 ≤ i ≤ m ai zi is a polynomial. To prove this, it is sufficient to show, for k ≥ 0 and f(z) = zk, it is true that f(T) = Tk, i.e.
for any suitable Γ enclosing σ(T). Choose Γ to be a circle of radius greater than the operator norm of T. As stated above, on such Γ, the resolvent map admits a power series representation
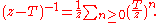
Substituting gives
which is
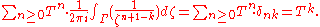
The δ is the Kronecker delta symbol.
We sketch an argument which invokes the first resolvent formula and the assumptions placed on ƒ. Start by calculating directly
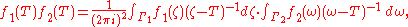
where the Jordan curves are chosen such that Γ1 lies in the inside of Γ2. The reason for this will be clear shortly. The above expression is equal to
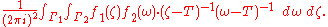
After applying the first resolvent formula, this becomes
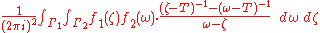
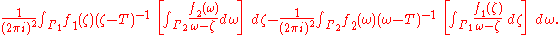
But the second term from above vanishes because ω ∈ Γ2 is in the outside of Γ1 and because ƒ1 is holomorphic on some open neighborhood of σ(T).
Thus,
For the same reason as above,
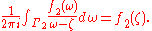
Therefore
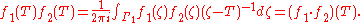
Assume for simplicity that Γ consists of only one Jordan curve. We estimate
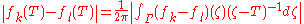
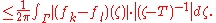
By combining the uniform convergence assumption and various continuity considerations, we see that the above tends to 0 as k, l → ∞. So {fk(T)} is Cauchy, therefore convergent.
has the following properties:
It can be proved that a calculus satisfying the above properties is unique.
We note that, everything discussed so far holds verbatim if the family of bounded operators L(X) is replaced by a Banach algebra
A. The functional calculus can be defined in exactly the same way for an element in A.
According to the homomorphism property, f(T) - f(μ) = (T - μ)g(T). Therefore μ ∈ σ(T) implies f(μ) ∈ σ(f(T)).
For the other inclusion, if μ is not in f(σ(T)), then the functional calculus is applicable to
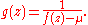
So g(T)(f(T) - μ) = I. Therefore μ does not lie in σ(f(T)).
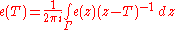
will be a bounded projection that commutes with T and provides a deal of useful information.
It transpires that this scenario is possible if and only if K is both open and closed in the subspace topology
on σ(T). Moreover the set V can be safely ignored since e is zero on it and therefore makes no contribution to the integral. The projection e(T) is called the spectral projection of T at K and is denoted by P(K;T). Thus every subset K of σ(T) that is both open and closed in the subspace topology has an associated spectral projection given by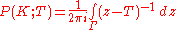
where Γ is a contour that encloses K but no other points of σ(T).
Since P = P(K;T) is bounded and commutes with T it enables T to be expressed in the form U ⊕ V where U = T|PX and V = T|(1-P)X. Both PX and (1-P)X are invariant subspaces of T moreover σ(U) = K and σ(V) = σ(T)\K. A key property is mutual orthogonality. If L is another open and closed set in the subspace topology on σ(T) then P(K;T)P(L;T) = P(L;T)P(K;T) = P(K ∩ L;T) which is zero whenever K and L are disjoint.
Spectral projections have numerous applications. Any isolated point of σ(T) is both open and closed in the subspace topology and therefore has an associated spectral projection. When X has finite dimension σ(T) consists of isolated points and the resultant spectral projections lead to a variant of Jordan normal form
wherein all the Jordan blocks corresponding to the same eigenvalue are consolidated. In other words there is precisely one block per distinct eigenvalue. The next section considers this decomposition in more detail.
Sometimes spectral projections inherit properties from their parent operators. For example if T is a positive matrix with spectral radius r then the Perron–Frobenius theorem
asserts that r ∈ σ(T). The associated spectral projection P = P(r;T) is also positive and by mutual orthogonality no other spectral projection can have a positive row or column. In fact TP = rP and (T/r)n → P as n → ∞ so this projection P (which is called the Perron projection) approximates Tn as n increases, and each of its columns is an eigenvector of T.
More generally if T is a compact operator then all non-zero points in σ(T) are isolated and so any finite subset of them can be used to decompose T. The associated spectral projection always has finite rank. Those operators in L(X) with similar spectral characteristics are known as Riesz operators
. Many classes of Riesz operators (including the compact operators) are ideals in L(X) and provide a rich field for research. However if X is a Hilbert space
there is exactly one closed ideal sandwiched between the Riesz operators and those of finite rank.
Much of the foregoing discussion can be set in the more general context of a complex Banach algebra
. Here spectral projections are referred to as spectral idempotents since there may no longer be a space for them to project onto.
Define ei to be 1 on some neighborhood that contains only the component Fi and 0 elsewhere. By the homomorphism property, ei(T) is a projection for all i. The relation ei(T) T = T ei(T) means the range of each ei(T), denoted by Xi, is an invariant subspace of T. Since
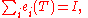
X can be expressed in terms of these complementary subspaces:
Similarly, if Ti is T restricted to Xi, then
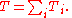
Consider the direct sum
With the norm
X' is a Banach space. The mapping R: X' → X defined by
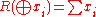
is a Banach space isomorphism, and we see that
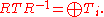
This can be viewed as a block diagonalization of T.
When X is finite dimensional, σ(T) = {λi} is a finite set of points in the complex plane. Choose ei to be 1 on an open disc containing only λi from the spectrum. The corresponding block-diagonal matrix
is the Jordan canonical form of T.
acting on a Hilbert space
, the domain of the functional calculus can be broadened. When comparing the two results, a rough analogy can be made with the relationship between the spectral theorem for normal matrices and the Jordan canonical form. When T is a normal operator, a continuous functional calculus
can be obtained, that is, one can evaluate f(T) with f being a continuous function
defined on σ(T). Using the machinery of measure theory, this can be extended to functions which are only measurable
(see Borel functional calculus
). In that context, if E ⊂ σ(T) is a Borel set and E(x) is the characteristic function of E, the projection operator E(T) is a refinement of ei(T) discussed above.
The Borel functional calculus extends to unbounded self-adjoint operators on a Hilbert space.
In slightly more abstract language, the holomorphic functional calculus can be extended to any element of a Banach algebra
, using essentially the same arguments as above. Similarly, the continuous functional calculus holds for normal elements in any C*-algebra and the measurable functional calculus for normal elements in any von Neumann algebra
.
s with non-empty resolvent set.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, holomorphic functional calculus is functional calculus
Functional calculus
In mathematics, a functional calculus is a theory allowing one to apply mathematical functions to mathematical operators. It is now a branch of the field of functional analysis, connected with spectral theory. In mathematics, a functional calculus is a theory allowing one to apply mathematical...
with holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s. That is to say, given a holomorphic function ƒ of a complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
argument z and an operator T, the aim is to construct an operator
which in a sense extends the function ƒ from complex argument to operator argument.
This article will discuss the case where T is a bounded linear operator on some Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
. In particular, T can be a square matrix with complex entries, a case which will be used to illustrate functional calculus and provide some heuristic insights for the assumptions involved in the general construction.
Need for a general functional calculus
In this section T will be assumed to be a n × n matrix with complex entries.If a given function ƒ is of certain special type, there are natural ways of defining ƒ(T). For instance, if
is a complex polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
, one can simply substitute T for z and define
where T0 = I, the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
. This is the polynomial functional calculus. It is a homomorphism from the ring of polynomials to the ring of n × n matrices.
Extending slightly from the polynomials, if
is holomorphic everywhere, i.e. an entire function
Entire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
, with MacLaurin series
mimicking the polynomial case suggests we define
Since the MacLaurin series converges everywhere, the above series will converge, in a chosen operator norm
Operator norm
In mathematics, the operator norm is a means to measure the "size" of certain linear operators. Formally, it is a norm defined on the space of bounded linear operators between two given normed vector spaces.- Introduction and definition :...
. An example of this is the exponential
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
of a matrix. Replacing z by T in the MacLaurin series of f(z) = ez gives
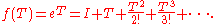
The requirement that the MacLaurin series of ƒ converges everywhere can be relaxed somewhat. From above it is evident that all that is really needed is the radius of convergence of the MacLaurin series be greater than
the operator norm of T. This enlarges somewhat the family of f for which ƒ(T) can be defined using the above approach. However it is not quite satisfactory. For instance, it is a fact from matrix theory that every non-singular T has a logarithm S in the sense that
It is desirable to have a functional calculus that allows one to define, for a non-singular T,
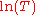
such that it coincides with S. This can not be done via power series. For example, the logarithmic series
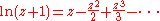
converges only on the open unit disk. Substituting T for z in the series fails to give a well-defined ln (T + I) for any invertible T + I with
Thus a more general functional calculus is needed.
Functional calculus and the spectrum
It is expected that a necessary condition for ƒ(T) to make sense is ƒ be defined on the spectrumSpectrum (functional analysis)
In functional analysis, the concept of the spectrum of a bounded operator is a generalisation of the concept of eigenvalues for matrices. Specifically, a complex number λ is said to be in the spectrum of a bounded linear operator T if λI − T is not invertible, where I is the...
of T. For example, the spectral theorem for normal matrices states every normal matrix is unitarily diagonalizable. There leads to a definition of ƒ(T) when T is normal. One encounters difficulties if ƒ(λ) is not defined for some eigenvalue λ of T.
Other indications also reinforce the idea that ƒ(T) can be defined only if ƒ is defined on the spectrum of T. If T is not invertible, then 0 is an eigenvalue. Since the natural logarithm is undefined at 0, one would expect that ln(T) can not be defined naturally. This is indeed the case. As another example, for
the reasonable way of calculating
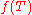would seem to beHowever, this expression is not defined if the inverses on the right-hand side do not exist, that is, if either 2 or 5 are eigenvalues of T.
For a given matrix T, the eigenvalues of T dictates to what extent ƒ(T) can be defined; ƒ(λ) must be defined for all eigenvalue λ of T. For a general bounded operator this condition translates to "ƒ must be defined on the spectrum
Spectrum (functional analysis)
In functional analysis, the concept of the spectrum of a bounded operator is a generalisation of the concept of eigenvalues for matrices. Specifically, a complex number λ is said to be in the spectrum of a bounded linear operator T if λI − T is not invertible, where I is the...
of T". This assumption turns out to be an enabling condition such that the functional calculus map
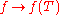
has certain desirable properties.
Functional calculus for a bounded operator
Recall the Cauchy integral formula from classical function theory. Let
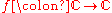
be holomorphic on some open
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
subset D in the complex plane, and
be a rectifiable Jordan curve in D, that is, a closed curve of finite length without self-intersections. Cauchy's integral formula states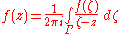for any z lying in the inside of Γ, i.e. the winding number
Winding number
In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...
of Γ about z is 1.
The idea is to extend this formula to functions taking values in the Banach space L(X). Cauchy's integral formula suggests the following definition (purely formal, for now):
where (ζ - T)-1 is the resolvent of T at ζ.
Assuming this Banach space-valued integral is appropriately defined, this proposed functional calculus implies the following necessary conditions:
- As the scalar version of Cauchy's integral formula applies to holomorphic f, we anticipate that is also the case for the Banach space case, where there should be a suitable notion of holomorphy for functions taking values in the Banach space L(X).
- As the resolvent mapping ζ → (ζ - T)-1 is undefined on the spectrum of T, σ(T), the Jordan curve Γ should not intersect σ(T). Furthermore, the resolvent mapping is holomorphic on the complement of σ(T). So, to obtain a non-trivial functional calculus, Γ must enclose, at least part of, σ(T).
- The functional calculus should be well-defined in the sense that f(T) is independent of Γ.
The full definition of the functional calculus is as follows: For T ∈ L(X), define
where f is a holomorphic function defined on an open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
D in the complex plane which contains σ(T), and
is a collection of Jordan curves in D such that σ(T) lies in the inside of Γ, and each γi is oriented in the positive sense.
The open set D may vary with ƒ and need not be connected, as shown by the figures on the right.
The following subsections make precise the notions invoked in the definition and show ƒ(T) is indeed well defined under given assumptions.
Banach space-valued integral
- Cf. Bochner integralBochner integralIn mathematics, the Bochner integral, named for Salomon Bochner, extends the definition of Lebesgue integral to functions that take values in a Banach space, as the limit of integrals of simple functions.-Definition:...
For a continuous function g defined in an open neighborhood of Γ and taking values in L(X), the contour integral ∫Γg is defined in the same way as for the scalar case. One can parametrize each γi ∈ Γ by a real interval [a, b], and the integral is the limit of the Riemann sums obtained from ever-finer partitions of [a, b]. The Riemann sums converge in the uniform operator topology
Operator topology
In the mathematical field of functional analysis there are several standard topologies which are given to the algebra B of bounded linear operators on a Hilbert space H.-Introduction:...
. We define
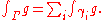
In the definition of the functional calculus, ƒ is assumed to be holomorphic in an open neighborhood of Γ. It will be shown below that the resolvent mapping is holomorphic on the resolvent set. Therefore the integral
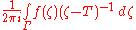
makes sense.
The resolvent mapping
The mapping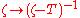is called the resolvent mapping of T. It is defined on the complement of σ(T), called the resolvent set of T and will be denoted by ρ(T).
Much of classical function theory depends on the properties of the integral
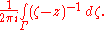
The holomorphic functional calculus is similar in that the resolvent mapping plays a crucial role in obtaining properties one requires from a nice functional calculus. This subsection outlines properties of the resolvent map that are essential in this context.
A resolvent formula
Direct calculation shows, for z1, z2 ∈ ρ(T),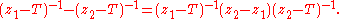Therefore
This equation is called the first resolvent formula. The formula shows (z1 − T)−1 and (z2 − T)−1 commute, which hints at the fact that the image of the functional calculus will be a commutative algebra. Letting z2 → z1 shows the resolvent map is (complex-) differentiable at each z1 ∈ ρ(T); so the integral in the expression of functional calculus converges in L(X).
Holomorphy
Stronger statement than differentiability can be made regarding the resolvent map. The resolvent set ρ(T) is actually an open set on which the resolvent map is holomorphic. This property will be used in subsequent arguments for the functional calculus. To verify this claim, let z1 ∈ ρ(T) and notice the formal expressionsuggests we consider
for (z2 − T)−1. The above series converges in L(X), which implies the existence of (z2 − T)−1, if
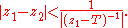
Therefore the resolvent set ρ(T) is open and the power series expression on an open disk centered at z1 ∈ ρ(T) shows the resolvent map is holomorphic on ρ(T).
Neumann series
Another expression for (z − T)−1 will also be useful. The formal expression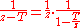leads one to consider
This series, the Neumann series, converges to (z − T)−1 if
Compactness of σ(T)
From the last two properties of the resolvent we can deduce that the spectrum σ(T) of a bounded operator T is a compact subset of the complex plane. Therefore for any open set D such that σ(T) ⊂ D, there exists a positively-oriented and smooth system of Jordan curves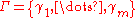such that σ(T) is in the inside of Γ and the complement of D is contained in the outside of Γ. Hence, for the definition of the functional calculus, indeed a suitable family of Jordan curves can be found for each f that is holomorphic on some D.
Well-definedness
The previous discussion has shown that the integral makes sense, i.e. a suitable collection Γ of Jordan curves does exist for each f and the integral does converge in the appropriate sense. What has not been shown is that the definition of the functional calculus is unambiguous, i.e. does not depend on the choice of Γ. This issue we now try to resolve.A preliminary fact
For a collection of Jordan curves Γ = {γ1... γm} and a point a in the complex plane C, the winding number of Γ with respect to a is the sum of the winding numbers of its elements. In symbols we put n(Γ, a) = ∑i n(γi, a). The following theorem is by Cauchy:Theorem Let G ⊂ C be an open set and Γ ⊂ G. If g: C → C be holomorphic on G, and for all a in the complement of G, n(Γ, a) = 0, then the contour integral ∫Γ g = 0.
We will need the vector-valued analog of this result when g takes values in L(X). To this end, let g: G → L(X) be holomorphic, with the same assumptions on Γ. The idea is use the dual space
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
L(X)* of L(X), and pass to Cauchy's theorem for the scalar case.
Consider the integral ∫Γ g ∈ L(X). If we can show, for all φ ∈ L(X)*, φ (∫Γ g) = 0, then the claim, that ∫Γ g = 0, follows. By boundedness of φ and the fact that the integral converges in norm,
But g is holomorphic implies the composition φ(g): G ⊂ C → C is holomorphic. So by Cauchy's theorem
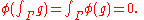
Main argument
The well-definedness of functional calculus now follows as an easy consequence. Let D be an open set containing σ(T). Suppose Γ = {γi} and Ω = {ωj} be two (finite) collections of Jordan curves satisfying the assumption given for the functional calculus. We wish to show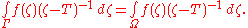Let Ω be obtained from Ω by reversing the orientation of each ωj, then
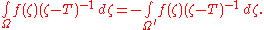
Consider the union of the two collections Γ ∪ Ω' . Both Γ ∪ Ω' and σ(T) are compact. So there is some open set U containing Γ ∪ Ω' such that σ(T) lies in the complement of U. Any a in the complement of U has winding number n(Γ ∪ Ω, a) = 0 and the function
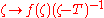
is holomorphic on U. So the vector-valued version of Cauchy's theorem gives
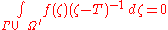
i.e.
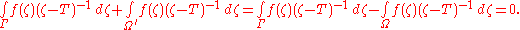
Hence the functional calculus is well-defined.
Consequently, if f1 and f2 are two holomorphic functions defined on corresponding neighborhoods D1 and D2 of σ(T) and they are equal on an open set containing σ(T), then f1(T) = f2(T). Moreover, even though the D1 may not be D2, the operator (f1 + f2) (T) is well-defined. Same holds for the definition of (f1·f2)(T).
On the assumption that f be holomorphic over an open neighborhood of σ(T)
It should perhaps be noted that so far the full strength of this assumption has not been utilized. For convergence of the integral, only continuity was used. For well-definedness, we only needed f be holomorphic on some open set U containing the contours Γ ∪ Ω' but not σ(T). The assumption will be applied in its entirety for showing the homomorphism property of the functional calculus.Polynomial case
The linearity of the map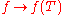follows from the convergence of the integral and that linear operations on a Banach space are continuous.
We recover the polynomial functional calculus when f(z) = ∑0 ≤ i ≤ m ai zi is a polynomial. To prove this, it is sufficient to show, for k ≥ 0 and f(z) = zk, it is true that f(T) = Tk, i.e.
for any suitable Γ enclosing σ(T). Choose Γ to be a circle of radius greater than the operator norm of T. As stated above, on such Γ, the resolvent map admits a power series representation
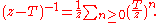
Substituting gives
which is
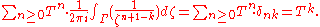
The δ is the Kronecker delta symbol.
The homomorphism property
For any ƒ1 and ƒ2 satisfying the appropriate assumptions, the homomorphism property statesWe sketch an argument which invokes the first resolvent formula and the assumptions placed on ƒ. Start by calculating directly
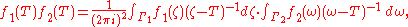
where the Jordan curves are chosen such that Γ1 lies in the inside of Γ2. The reason for this will be clear shortly. The above expression is equal to
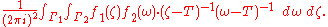
After applying the first resolvent formula, this becomes
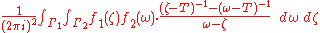
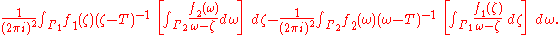
But the second term from above vanishes because ω ∈ Γ2 is in the outside of Γ1 and because ƒ1 is holomorphic on some open neighborhood of σ(T).
Thus,
For the same reason as above,
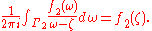
Therefore
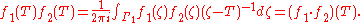
Continuity with respect to compact convergence
Let G ⊂ C be open with σ(T) ⊂ G. Suppose a sequence {fk} of holomorphic functions on G converges uniformly on compact subsets of G (this is sometimes called compact convergence). Then {fk(T)} is convergent in L(X):Assume for simplicity that Γ consists of only one Jordan curve. We estimate
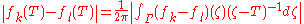
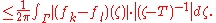
By combining the uniform convergence assumption and various continuity considerations, we see that the above tends to 0 as k, l → ∞. So {fk(T)} is Cauchy, therefore convergent.
Uniqueness
To summarize, we have shown the holomorphic functional calculushas the following properties:
- It extends the polynomial functional calculus.
- It is an algebra homomorphism from the algebra of holomorphic functions defined on a neighborhood of σ(T) to L(X)
- It preserves uniform convergence on compact sets.
It can be proved that a calculus satisfying the above properties is unique.
We note that, everything discussed so far holds verbatim if the family of bounded operators L(X) is replaced by a Banach algebra
Banach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
A. The functional calculus can be defined in exactly the same way for an element in A.
Spectral considerations
The above demonstrates the intimate relationship between the holomorphic functional calculus of a given T ∈ L(X) and σ(T). This is true in general. Under more restrictive assumptions, the spectral theorem for bounded normal operators (see below) can be reformulated in terms of a functional calculus. This section sketches some results in this direction.Spectral mapping theorem
It is known that the spectral mapping theorem holds for the polynomial functional calculus: for any polynomial p, σ(p(T)) = p(σ(T)). This can be extended to the holomorphic calculus. To show f(σ(T)) ⊂ σ(f(T)), let μ be any complex number. By a result from complex analysis, there exists a function g holomorphic on a neighborhood of σ(T) such thatAccording to the homomorphism property, f(T) - f(μ) = (T - μ)g(T). Therefore μ ∈ σ(T) implies f(μ) ∈ σ(f(T)).
For the other inclusion, if μ is not in f(σ(T)), then the functional calculus is applicable to
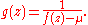
So g(T)(f(T) - μ) = I. Therefore μ does not lie in σ(f(T)).
Spectral projections
The underlying idea is as follows. Suppose that K is a subset of σ(T) and U,V are disjoint neighbourhoods of K and σ(T)\K respectively. Define e(z) = 1 if z ∈ U and e(z) = 0 if z ∈ V. Then e is a holomorphic function with [e(z)]2 = e(z) and so, for a suitable contour Γ which lies in U ∪ V and which encloses σ(T), the linear operator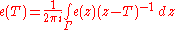will be a bounded projection that commutes with T and provides a deal of useful information.
It transpires that this scenario is possible if and only if K is both open and closed in the subspace topology
Subspace topology
In topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
on σ(T). Moreover the set V can be safely ignored since e is zero on it and therefore makes no contribution to the integral. The projection e(T) is called the spectral projection of T at K and is denoted by P(K;T). Thus every subset K of σ(T) that is both open and closed in the subspace topology has an associated spectral projection given by
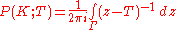
where Γ is a contour that encloses K but no other points of σ(T).
Since P = P(K;T) is bounded and commutes with T it enables T to be expressed in the form U ⊕ V where U = T|PX and V = T|(1-P)X. Both PX and (1-P)X are invariant subspaces of T moreover σ(U) = K and σ(V) = σ(T)\K. A key property is mutual orthogonality. If L is another open and closed set in the subspace topology on σ(T) then P(K;T)P(L;T) = P(L;T)P(K;T) = P(K ∩ L;T) which is zero whenever K and L are disjoint.
Spectral projections have numerous applications. Any isolated point of σ(T) is both open and closed in the subspace topology and therefore has an associated spectral projection. When X has finite dimension σ(T) consists of isolated points and the resultant spectral projections lead to a variant of Jordan normal form
Jordan normal form
In linear algebra, a Jordan normal form of a linear operator on a finite-dimensional vector space is an upper triangular matrix of a particular form called Jordan matrix, representing the operator on some basis...
wherein all the Jordan blocks corresponding to the same eigenvalue are consolidated. In other words there is precisely one block per distinct eigenvalue. The next section considers this decomposition in more detail.
Sometimes spectral projections inherit properties from their parent operators. For example if T is a positive matrix with spectral radius r then the Perron–Frobenius theorem
Perron–Frobenius theorem
In linear algebra, the Perron–Frobenius theorem, proved by and , asserts that a real square matrix with positive entries has a unique largest real eigenvalue and that the corresponding eigenvector has strictly positive components, and also asserts a similar statement for certain classes of...
asserts that r ∈ σ(T). The associated spectral projection P = P(r;T) is also positive and by mutual orthogonality no other spectral projection can have a positive row or column. In fact TP = rP and (T/r)n → P as n → ∞ so this projection P (which is called the Perron projection) approximates Tn as n increases, and each of its columns is an eigenvector of T.
More generally if T is a compact operator then all non-zero points in σ(T) are isolated and so any finite subset of them can be used to decompose T. The associated spectral projection always has finite rank. Those operators in L(X) with similar spectral characteristics are known as Riesz operators
Frigyes Riesz
Frigyes Riesz was a mathematician who was born in Győr, Hungary and died in Budapest, Hungary. He was rector and professor at University of Szeged...
. Many classes of Riesz operators (including the compact operators) are ideals in L(X) and provide a rich field for research. However if X is a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
there is exactly one closed ideal sandwiched between the Riesz operators and those of finite rank.
Much of the foregoing discussion can be set in the more general context of a complex Banach algebra
Banach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
. Here spectral projections are referred to as spectral idempotents since there may no longer be a space for them to project onto.
Invariant subspace decomposition
If the spectrum σ(T) is not connected, X can be decomposed into invariant subspaces of T using the functional calculus. Let σ(T) be a disjoint unionDefine ei to be 1 on some neighborhood that contains only the component Fi and 0 elsewhere. By the homomorphism property, ei(T) is a projection for all i. The relation ei(T) T = T ei(T) means the range of each ei(T), denoted by Xi, is an invariant subspace of T. Since
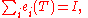
X can be expressed in terms of these complementary subspaces:
Similarly, if Ti is T restricted to Xi, then
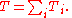
Consider the direct sum
With the norm
X' is a Banach space. The mapping R: X' → X defined by
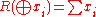
is a Banach space isomorphism, and we see that
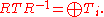
This can be viewed as a block diagonalization of T.
When X is finite dimensional, σ(T) = {λi} is a finite set of points in the complex plane. Choose ei to be 1 on an open disc containing only λi from the spectrum. The corresponding block-diagonal matrix
is the Jordan canonical form of T.
Related results
With stronger assumptions, when T is a normal operatorNormal operator
In mathematics, especially functional analysis, a normal operator on a complex Hilbert space H is a continuous linear operatorN:H\to Hthat commutes with its hermitian adjoint N*: N\,N^*=N^*N....
acting on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
, the domain of the functional calculus can be broadened. When comparing the two results, a rough analogy can be made with the relationship between the spectral theorem for normal matrices and the Jordan canonical form. When T is a normal operator, a continuous functional calculus
Continuous functional calculus
In mathematics, the continuous functional calculus of operator theory and C*-algebra theory allows applications of continuous functions to normal elements of a C*-algebra. More precisely,Theorem...
can be obtained, that is, one can evaluate f(T) with f being a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
defined on σ(T). Using the machinery of measure theory, this can be extended to functions which are only measurable
Measurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
(see Borel functional calculus
Borel functional calculus
In functional analysis, a branch of mathematics, the Borel functional calculus is a functional calculus , which has particularly broad scope. Thus for instance if T is an operator, applying the squaring function s → s2 to T yields the operator T2...
). In that context, if E ⊂ σ(T) is a Borel set and E(x) is the characteristic function of E, the projection operator E(T) is a refinement of ei(T) discussed above.
The Borel functional calculus extends to unbounded self-adjoint operators on a Hilbert space.
In slightly more abstract language, the holomorphic functional calculus can be extended to any element of a Banach algebra
Banach algebra
In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
, using essentially the same arguments as above. Similarly, the continuous functional calculus holds for normal elements in any C*-algebra and the measurable functional calculus for normal elements in any von Neumann algebra
Von Neumann algebra
In mathematics, a von Neumann algebra or W*-algebra is a *-algebra of bounded operators on a Hilbert space that is closed in the weak operator topology and contains the identity operator. They were originally introduced by John von Neumann, motivated by his study of single operators, group...
.
Unbounded operators
A holomorphic functional calculus can be defined in a similar fashion for unbounded closed operatorClosed operator
In mathematics, specifically in functional analysis, closed linear operators are an important class of linear operators on Banach spaces. They are more general than bounded operators, and therefore not necessarily continuous, but they still retain nice enough properties that one can define the...
s with non-empty resolvent set.
See also
- Resolvent formalismResolvent formalismIn mathematics, the resolvent formalism is a technique for applying concepts from complex analysis to the study of the spectrum of operators on Hilbert spaces and more general spaces....
- Jordan canonical form, where the finite dimensional case is discussed in some detail.