Operator topology
Encyclopedia
In the mathematical
field of functional analysis
there are several standard topologies
which are given to the algebra B(H) of bounded linear operators on a Hilbert space
H.
All of these notions make sense and are useful for a Banach space
in place of the Hilbert space H.
There are many topologies that can be defined on B(H) besides the ones used above. These topologies are all locally convex, which implies that they are defined by a family of seminorms.
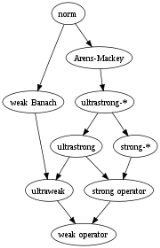
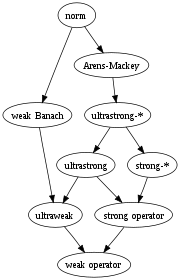
In analysis, a topology is called strong if it has many open sets and weak if it has few open sets, so that the corresponding modes of convergence are, respectively, strong and weak. (In topology proper, these terms can suggest the opposite meaning, so strong and weak are replaced with, respectively, fine and coarse.) The diagram on the right is a summary of the relations, with the arrows pointing from strong to weak.
The Banach space
B(H) has a (unique) predual
B(H)*,
consisting of the trace class operators, whose dual is B(H). The seminorm pw(x) for w positive in the predual is defined to be
(w, x*x)1/2.
If B is a vector space of linear maps on the vector space A, then σ(A, B) is defined to be the weakest topology on A such that all elements of B are continuous.
(xh1, h2) for h1, h2 in H. The continuous linear functionals on B(H) for the ultraweak, ultrastrong, ultrastrong* and Arens-Mackey topologies are the same, and are the elements of the predual B(H)*.
By definition, the continuous linear functionals in the norm topology are the same as those in the weak Banach space topology.
This dual is a rather large space with many pathological elements.
On norm bounded sets of B(H), the weak (operator) and ultraweak topologies coincide. This can be seen via, for instance, the Banach–Alaoglu theorem. For essentially the same reason, the ultrastrong
topology is the same as the strong topology on any (norm) bounded subset of B(H). Same is true for the Arens-Mackey topology, the ultrastrong*, and the strong* topology.
In locally convex spaces, closure of convex sets can be characterized by the continuous linear functionals. Therefore, for a convex
subset K of B(H), the conditions that K be closed in the ultrastrong*, ultrastrong, and ultraweak topologies are all equivalent and are also equivalent to the conditions that
for all r > 0, K has closed intersection with the closed ball of radius r in the strong*, strong, or weak (operator) topologies.
The norm topology is metrizable and the others are not; in fact they fail to be first-countable. However, when H is separable, all the topologies above are metrizable when restricted to the unit ball (or to any norm-bounded subset).
. The norm topology is fundamental because it makes B(H) into a Banach space, but it is too strong for many purposes; for example, B(H) is not separable in this topology. The strong operator topology could be the most commonly used.
The ultraweak and ultrastrong topologies are better-behaved than the weak and strong operator topologies, but their definitions are more complicated, so they are usually not used unless their better properties are really needed. For example, the dual space of B(H) in the weak or strong operator topology is too small to have much analytic content.
The adjoint map is not continuous in the strong operator and ultrastrong topologies, while the strong* and ultrastrong* topologies are modifications so that the adjoint becomes continuous. They are not used very often.
The Arens-Mackey topology and the weak Banach space topology are relatively rarely used.
To summarize, the three essential topologies on B(H) are the norm, ultrastrong, and ultraweak topologies. The weak and strong operator topologies are widely used as convenient approximations to the ultraweak and ultrastrong topologies. The other topologies are relatively obscure.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
there are several standard topologies
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
which are given to the algebra B(H) of bounded linear operators on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
H.
Introduction
Let {Tn} be a sequence of linear operators on the Hilbert space H. Consider the statement that Tn converges to some operator T in H. This could have several different meanings:- If
, that is, the operator normOperator normIn mathematics, the operator norm is a means to measure the "size" of certain linear operators. Formally, it is a norm defined on the space of bounded linear operators between two given normed vector spaces.- Introduction and definition :...
of Tn - T (the supremum of
, where x ranges over the unit ball in H) converges to 0, we say that 
in the uniform operator topology. - If
for all x in H, then we say 
in the strong operator topology. - Finally, suppose
in the weak topologyWeak topologyIn mathematics, weak topology is an alternative term for initial topology. The term is most commonly used for the initial topology of a topological vector space with respect to its continuous dual...
of H. This means that
for all linear functionals F on H. In this case we say that 
in the weak operator topology.
All of these notions make sense and are useful for a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
in place of the Hilbert space H.
List of topologies on B(H)
In analysis, a topology is called strong if it has many open sets and weak if it has few open sets, so that the corresponding modes of convergence are, respectively, strong and weak. (In topology proper, these terms can suggest the opposite meaning, so strong and weak are replaced with, respectively, fine and coarse.) The diagram on the right is a summary of the relations, with the arrows pointing from strong to weak.
The Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
B(H) has a (unique) predual
Predual
In mathematics, the predual of an object D is an object P whose dual space is D.For example, the predual of the space of bounded operators is the space of trace class operators. The predual of the space of differential forms is the space of chainlets....
B(H)*,
consisting of the trace class operators, whose dual is B(H). The seminorm pw(x) for w positive in the predual is defined to be
(w, x*x)1/2.
If B is a vector space of linear maps on the vector space A, then σ(A, B) is defined to be the weakest topology on A such that all elements of B are continuous.
- The norm topology or uniform topology or uniform operator topology is defined by the usual norm ||x|| on B(H). It is stronger than all the other topologies below.
- The weak (Banach space) topologyWeak topologyIn mathematics, weak topology is an alternative term for initial topology. The term is most commonly used for the initial topology of a topological vector space with respect to its continuous dual...
is σ(B(H), B(H)*), in other words the weakest topology such that all elements of the dual B(H)* are continuous. It is the weak topology on the Banach space B(H). It is stronger than the ultraweak and weak operator topologies. (Warning: the weak Banach space topology and the weak operator topology and the ultraweak topology are all sometimes called the weak topology, but they are different.) - The Mackey topologyMackey topologyIn functional analysis and related areas of mathematics, the Mackey topology, named after George Mackey, is the finest topology for a topological vector space which still preserves the continuous dual...
or Arens-Mackey topology is the strongest locally convex topology on B(H) such that the dual is B(H)*, and is also the uniform convergence topology on σ(B(H)*, B(H)-compact convex subsets of B(H)*. It is stronger than all topologies below. - The σ-strong* topology or ultrastrong* topology is the weakest topology stronger than the ultrastrong topology such that the adjoint map is continuous. It is defined by the family of seminorms pw(x) and pw(x*) for positive elements w of B(H)*. It is stronger than all topologies below.
- The σ-strong topology or ultrastrong topology or strongest topology or strongest operator topology is defined by the family of seminorms pw(x) for positive elements w of B(H)*. It is stronger than all the topologies below other than the strong* topology. Warning: in spite of the name "strongest topology", it is weaker than the norm topology.)
- The σ-weak topology or ultraweak topology or weak* operator topology or weak * topology or weak topology or σ(B(H), B(H)*) topology is defined by the family of seminorms |(w, x)| for elements w of B(H)*. It is stronger than the weak operator topology. (Warning: the weak Banach space topology and the weak operator topology and the ultraweak topology are all sometimes called the weak topology, but they are different.)
- The strong* operator topology or strong* topology is defined by the seminorms ||x(h)|| and ||x*(h)|| for h in H. It is stronger than the strong and weak operator topologies.
- The strong operator topologyStrong operator topologyIn functional analysis, a branch of mathematics, the strong operator topology, often abbreviated SOT, is the weakest locally convex topology on the set of bounded operators on a Hilbert space such that the evaluation map sending an operator T to the real number \|Tx\| is continuous for each vector...
(SOT) or strong topology is defined by the seminorms ||x(h)|| for h in H. It is stronger than the weak operator topology. - The weak operator topologyWeak operator topologyIn functional analysis, the weak operator topology, often abbreviated WOT, is the weakest topology on the set of bounded operators on a Hilbert space H, such that the functional sending an operator T to the complex number is continuous for any vectors x and y in the Hilbert space.Equivalently, a...
(WOT) or weak topology is defined by the seminorms |(x(h1), h2)| for h1 and h2 in H. (Warning: the weak Banach space topology, the weak operator topology, and the ultraweak topology are all sometimes called the weak topology, but they are different.)
Relations between the topologies
The continuous linear functionals on B(H) for the weak, strong, and strong* (operator) topologies are the same, and are the finite linear combinations of the linear functionals(xh1, h2) for h1, h2 in H. The continuous linear functionals on B(H) for the ultraweak, ultrastrong, ultrastrong* and Arens-Mackey topologies are the same, and are the elements of the predual B(H)*.
By definition, the continuous linear functionals in the norm topology are the same as those in the weak Banach space topology.
This dual is a rather large space with many pathological elements.
On norm bounded sets of B(H), the weak (operator) and ultraweak topologies coincide. This can be seen via, for instance, the Banach–Alaoglu theorem. For essentially the same reason, the ultrastrong
topology is the same as the strong topology on any (norm) bounded subset of B(H). Same is true for the Arens-Mackey topology, the ultrastrong*, and the strong* topology.
In locally convex spaces, closure of convex sets can be characterized by the continuous linear functionals. Therefore, for a convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
subset K of B(H), the conditions that K be closed in the ultrastrong*, ultrastrong, and ultraweak topologies are all equivalent and are also equivalent to the conditions that
for all r > 0, K has closed intersection with the closed ball of radius r in the strong*, strong, or weak (operator) topologies.
The norm topology is metrizable and the others are not; in fact they fail to be first-countable. However, when H is separable, all the topologies above are metrizable when restricted to the unit ball (or to any norm-bounded subset).
Which topology should I use?
The most commonly used topologies are the norm, strong, and weak operator topologies. The weak operator topology is useful for compactness arguments, because the unit ball is compact by the Banach-Alaoglu theoremBanach-Alaoglu theorem
In functional analysis and related branches of mathematics, the Banach–Alaoglu theorem states that the closed unit ball of the dual space of a normed vector space is compact in the weak* topology. A common proof identifies the unit ball with the weak* topology as a closed subset of a product of...
. The norm topology is fundamental because it makes B(H) into a Banach space, but it is too strong for many purposes; for example, B(H) is not separable in this topology. The strong operator topology could be the most commonly used.
The ultraweak and ultrastrong topologies are better-behaved than the weak and strong operator topologies, but their definitions are more complicated, so they are usually not used unless their better properties are really needed. For example, the dual space of B(H) in the weak or strong operator topology is too small to have much analytic content.
The adjoint map is not continuous in the strong operator and ultrastrong topologies, while the strong* and ultrastrong* topologies are modifications so that the adjoint becomes continuous. They are not used very often.
The Arens-Mackey topology and the weak Banach space topology are relatively rarely used.
To summarize, the three essential topologies on B(H) are the norm, ultrastrong, and ultraweak topologies. The weak and strong operator topologies are widely used as convenient approximations to the ultraweak and ultrastrong topologies. The other topologies are relatively obscure.