Measurable function
Encyclopedia
In mathematics
, particularly in measure theory, measurable functions are structure-preserving functions
between measurable spaces; as such, they form a natural context for the theory of integration
. Specifically, a function between measurable spaces is said to be measurable if the preimage of each measurable set is measurable, analogous to the situation of continuous functions between topological space
s.
This definition can be deceptively simple, however, as special care must be taken regarding the
-algebras
involved. In particular, when a function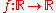
is said to be Lebesgue measurable what is actually meant is that
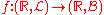is a measurable function—that is, the domain and range represent different 
-algebras on the same underlying set (here 
is the sigma algebra of Lebesgue measurable sets, and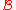 
is the Borel algebra
on
). As a result, the composition of Lebesgue-measurable functions need not be Lebesgue-measurable.
By convention a topological space
is assumed to be equipped with the Borel algebra
generated by its open subsets unless otherwise specified. Most commonly this space will be the real or complex numbers. For instance, a real-valued measurable function is a function for which the preimage of each Borel set
is measurable. A complex-valued measurable function is defined analogously. In practice, some authors use measurable functions to refer only to real-valued measurable functions with respect to the Borel algebra.
If the values of the function lie in an infinite-dimensional vector space instead of R or C, usually other definitions of measurability are used, such as weak measurability and Bochner measurability.
In probability theory
, the sigma algebra often represents the set of available information, and a function (in this context a random variable
) is measurable if and only if it represents an outcome that is knowable based on the available information. In contrast, functions that are not Lebesgue measurable are generally considered pathological
, at least in the field of analysis
.
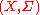and 
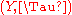be measurable spaces, meaning that 
and 
are sets equipped with respective sigma algebras 
and 
. A function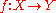
is said to be measurable if
for every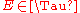 
. The notion of measurability depends on the sigma algebras 
and 
. To emphasize this dependency, if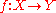 
is a measurable function, we will write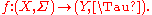
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly in measure theory, measurable functions are structure-preserving functions
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
between measurable spaces; as such, they form a natural context for the theory of integration
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
. Specifically, a function between measurable spaces is said to be measurable if the preimage of each measurable set is measurable, analogous to the situation of continuous functions between topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s.
This definition can be deceptively simple, however, as special care must be taken regarding the
-algebrasSigma-algebra
In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
involved. In particular, when a function
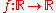is said to be Lebesgue measurable what is actually meant is that 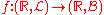is a measurable function—that is, the domain and range represent different -algebras on the same underlying set (here is the sigma algebra of Lebesgue measurable sets, and 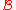is the Borel algebraBorel algebra
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
on
). As a result, the composition of Lebesgue-measurable functions need not be Lebesgue-measurable.By convention a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
is assumed to be equipped with the Borel algebra
Borel algebra
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
generated by its open subsets unless otherwise specified. Most commonly this space will be the real or complex numbers. For instance, a real-valued measurable function is a function for which the preimage of each Borel set
Borel set
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
is measurable. A complex-valued measurable function is defined analogously. In practice, some authors use measurable functions to refer only to real-valued measurable functions with respect to the Borel algebra.
If the values of the function lie in an infinite-dimensional vector space instead of R or C, usually other definitions of measurability are used, such as weak measurability and Bochner measurability.
In probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, the sigma algebra often represents the set of available information, and a function (in this context a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
) is measurable if and only if it represents an outcome that is knowable based on the available information. In contrast, functions that are not Lebesgue measurable are generally considered pathological
Pathological (mathematics)
In mathematics, a pathological phenomenon is one whose properties are considered atypically bad or counterintuitive; the opposite is well-behaved....
, at least in the field of analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
.
Formal definition
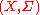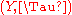Let and be measurable spaces, meaning that and are sets equipped with respective sigma algebras and . A function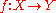is said to be measurable if
for every 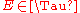. The notion of measurability depends on the sigma algebras and . To emphasize this dependency, if 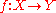is a measurable function, we will write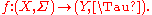Special measurable functions
- If
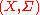and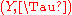 
are Borel spaces, a measurable function 
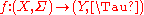is also called a Borel function. Continuous functions are Borel functions but not all Borel functions are continuous. However, a measurable function is nearly a continuous function; see Luzin's theoremLuzin's theoremIn mathematics, Lusin's theorem in real analysis is a form of Littlewood's second principle.It states that every measurable function is a continuous function on nearly all its domain:...
. If a Borel function happens to be a section of some map
, it is called a Borel section.
- A Lebesgue measurable function is a measurable function
, where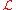 
is the sigma algebra of Lebesgue measurable sets, and 
is the Borel algebraBorel algebraIn mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
on the complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s
. Lebesgue measurable functions are of interest in mathematical analysisMathematical analysisMathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
because they can be integratedLebesgue integrationIn mathematics, Lebesgue integration, named after French mathematician Henri Lebesgue , refers to both the general theory of integration of a function with respect to a general measure, and to the specific case of integration of a function defined on a subset of the real line or a higher...
.
- Random variableRandom variableIn probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s are by definition measurable functions defined on sample spaces.
Properties of measurable functions
- The sum and product of two complex-valued measurable functions are measurable. So is the quotient, so long as there is no division by zero.
- The composition of measurable functions is measurable; i.e., if
and 
are measurable functions, then so is 
. But see the caveat regarding Lebesgue-measurable functions in the introduction.
- The (pointwise) supremumSupremumIn mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
, infimumInfimumIn mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
, limit superior, and limit inferior of a sequence (viz., countably many) of real-valued measurable functions are all measurable as well.
- The pointwisePointwiseIn mathematics, the qualifier pointwise is used to indicate that a certain property is defined by considering each value f of some function f. An important class of pointwise concepts are the pointwise operations — operations defined on functions by applying the operations to function values...
limit of a sequence of measurable functions is measurable; note that the corresponding statement for continuous functions requires stronger conditions than pointwise convergence, such as uniform convergence. (This is correct when the counter domain of the elements of the sequence is a metric space. It is false in general; see pages 125 and 126 of.)
Non-measurable functions
Real-valued functions encountered in applications tend to be measurable; however, it is not difficult to find non-measurable functions.- So long as there are non-measurable sets in a measure space, there are non-measurable functions from that space. If
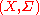is some measurable space and 
is a non-measurableNon-measurable setIn mathematics, a non-measurable set is a set whose structure is so complicated that it cannot be assigned any meaningful measure. Such sets are constructed to shed light on the notions of length, area and volume in formal set theory....
set, i.e. if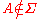
, then the indicator function 
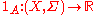is non-measurable (where 
is equipped with the Borel algebraBorel algebraIn mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
as usual), since the preimage of the measurable set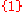
is the non-measurable set 
. Here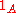 
is given by
-
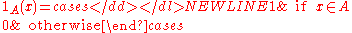
- Any non-constant function can be made non-measurable by equipping the domain and range with appropriate
-algebras. If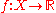 
is an arbitrary non-constant, real-valued function, then 
is non-measurable if 
is equipped with the indiscrete algebra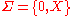 
, since the preimage of any point in the range is some proper, nonempty subset of 
, and therefore does not lie in 
.
See also
- Vector spaces of measurable functions: the
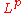spacesLp spaceIn mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces... - Measure-preserving dynamical systemMeasure-preserving dynamical systemIn mathematics, a measure-preserving dynamical system is an object of study in the abstract formulation of dynamical systems, and ergodic theory in particular.-Definition:...
- Any non-constant function can be made non-measurable by equipping the domain and range with appropriate