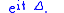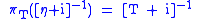Borel functional calculus
Encyclopedia
In functional analysis
, a branch of mathematics
, the Borel functional calculus is a functional calculus
(that is, an assignment of operators from commutative algebras to functions defined on their spectrum
), which has particularly broad scope. Thus for instance if T is an operator, applying the squaring function s → s2 to T yields the operator T2. Using the functional calculus for larger classes of functions, we can for example define rigorously the "square root" of the (negative) Laplacian operator −Δ or the exponential
The 'scope' here means the kind of function of an operator which is allowed. The Borel functional calculus is more general than the continuous functional calculus
.
More precisely, the Borel functional calculus allows us to apply an arbitrary Borel function to a self-adjoint operator
, in a way which generalizes applying a polynomial function.
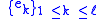
consisting of eigenvectors of T, that is
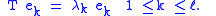
Thus, for any positive integer n,
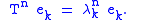
In this case, given a Borel function h, we can define an operator h(T) by specifying its behavior on the basis:
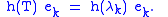
In general, any self-adjoint operator T is unitarily equivalent
to a multiplication operator; this means that for many purposes, T can be considered as an operator
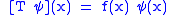
acting on L2 of some measure space. The domain of T consists of those functions for which the above expression is in L2. In this case, we can define analogously

For many technical purposes, the preceding formulation is good enough. However, it is desirable to formulate the functional calculus in a way in which it is clear that it does not depend on the particular representation of T as a multiplication operator. This we do in the next section.
H is a mapping defined on the space of bounded complex-valued Borel functions f on the real line,

such that the following conditions hold
Theorem. Any self-adjoint operator T has a unique Borel functional calculus.
This defines the functional calculus for bounded functions applied to possibly unbounded self-adjoint operators. Using the bounded functional calculus, one can prove part of the Stone's theorem on one-parameter unitary groups
:
Theorem. If A is a self-adjoint operator, then
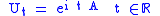
is a 1-parameter strongly continuous unitary group whose infinitesimal generator is i A.
As an application, we consider the Schrödinger equation
, or equivalently, the dynamics
of a quantum mechanical system. In non-relativistic
quantum mechanics
, the Hamiltonian
operator H models the total energy
observable
of a quantum mechanical system S. The unitary group generated by i H corresponds to the time evolution of S.
We can also use the Borel functional calculus to abstractly solve some linear initial value problem
s such as the heat equation, or Maxwell's equations.
First pass from polynomial to continuous functional calculus
by using the Stone-Weierstrass theorem
. The crucial fact here is that, for a bounded self adjoint operator T and a polynomial p,
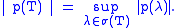
Consequently, the mapping
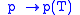
is an isometry and a densely defined homomorphism on the ring of polynomial functions. Extending by continuity defines f(T) for a continuous function f on the spectrum of T. The Riesz-Markov theorem then allows us to pass from integration on continuous functions to spectral measures, and this is the Borel functional calculus.
Alternatively, the continuous calculus can be obtained via the Gelfand transform, in the context of commutative Banach algebras. Extending to measurable functions is achieved by applying Riesz-Markov, as above. In this formulation, T can be a normal operator
.
Given an operator T, the range of the continuous functional calculus h → h(T) is the (abelian) C*-algebra C(T) generated by T. The Borel functional calculus has a larger range, that is the closure of C(T) in the weak operator topology
, a (still abelian) von Neumann algebra
.
Theorem. Let T be a self-adjoint operator on H, h a real-valued Borel function on R. There is a unique operator S such that
The operator S of the previous theorem is denoted h(T).
More generally, a Borel functional calculus also exists for (bounded) normal operators.

is a projection-valued measure
called the resolution of the identity for the self adjoint operator T. The measure of R with respect to Ω is the identity operator on H. In other words, the identity operator can be expressed as the spectral integral I = ∫ 1 dΩ. Sometimes the term "resolution of the identity" is also used to describe this representation of the identity operator as a spectral integral.
In the case of a discrete measure (in particular, when H is finite dimensional), I = ∫ 1 dΩ can be written as
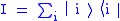
in the Dirac notation, where each |i> is a normalized eigenvector of T. The set { |i⟩ } is an orthonormal basis of H.
In physics literature, using the above as heuristic, one passes to the case when the spectral measure is no longer discrete and write the resolution of identity as
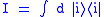
and speak of a "continuous basis", or "continuum of basis states", { |i⟩ }. Mathematically, unless rigorous justifications are given, this expression is purely formal.
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Borel functional calculus is a functional calculus
Functional calculus
In mathematics, a functional calculus is a theory allowing one to apply mathematical functions to mathematical operators. It is now a branch of the field of functional analysis, connected with spectral theory. In mathematics, a functional calculus is a theory allowing one to apply mathematical...
(that is, an assignment of operators from commutative algebras to functions defined on their spectrum
Spectrum of a ring
In abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
), which has particularly broad scope. Thus for instance if T is an operator, applying the squaring function s → s2 to T yields the operator T2. Using the functional calculus for larger classes of functions, we can for example define rigorously the "square root" of the (negative) Laplacian operator −Δ or the exponential
The 'scope' here means the kind of function of an operator which is allowed. The Borel functional calculus is more general than the continuous functional calculus
Continuous functional calculus
In mathematics, the continuous functional calculus of operator theory and C*-algebra theory allows applications of continuous functions to normal elements of a C*-algebra. More precisely,Theorem...
.
More precisely, the Borel functional calculus allows us to apply an arbitrary Borel function to a self-adjoint operator
Self-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
, in a way which generalizes applying a polynomial function.
Motivation
If T is a self-adjoint operator on a finite dimensional inner product space H, H has an orthonormal basisOrthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
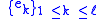
consisting of eigenvectors of T, that is
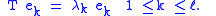
Thus, for any positive integer n,
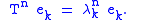
In this case, given a Borel function h, we can define an operator h(T) by specifying its behavior on the basis:
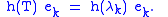
In general, any self-adjoint operator T is unitarily equivalent
Self-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
to a multiplication operator; this means that for many purposes, T can be considered as an operator
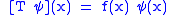
acting on L2 of some measure space. The domain of T consists of those functions for which the above expression is in L2. In this case, we can define analogously

For many technical purposes, the preceding formulation is good enough. However, it is desirable to formulate the functional calculus in a way in which it is clear that it does not depend on the particular representation of T as a multiplication operator. This we do in the next section.
The bounded functional calculus
Formally, the bounded Borel functional calculus of a self adjoint operator T on Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
H is a mapping defined on the space of bounded complex-valued Borel functions f on the real line,

such that the following conditions hold
- πT is an involution preserving and unit-preserving homomorphism from the ring of complex-valued bounded measurable functions on R.
- If ξ is an element of H, then
- is a countably additive measure on the Borel sets of R. In the above formula 1E denotes the indicator function of E. These measures νξ are called the spectral measures of T.
- where η denotes the mapping z → z on C.
Theorem. Any self-adjoint operator T has a unique Borel functional calculus.
This defines the functional calculus for bounded functions applied to possibly unbounded self-adjoint operators. Using the bounded functional calculus, one can prove part of the Stone's theorem on one-parameter unitary groups
Stone's theorem on one-parameter unitary groups
In mathematics, Stone's theorem on one-parameter unitary groups is a basic theorem of functional analysis which establishes a one-to-one correspondence between self-adjoint operators on a Hilbert space H and one-parameter families of unitary operators...
:
Theorem. If A is a self-adjoint operator, then
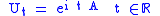
is a 1-parameter strongly continuous unitary group whose infinitesimal generator is i A.
As an application, we consider the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
, or equivalently, the dynamics
Dynamics (mechanics)
In the field of physics, the study of the causes of motion and changes in motion is dynamics. In other words the study of forces and why objects are in motion. Dynamics includes the study of the effect of torques on motion...
of a quantum mechanical system. In non-relativistic
Theory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, the Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
operator H models the total energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
observable
Observable
In physics, particularly in quantum physics, a system observable is a property of the system state that can be determined by some sequence of physical operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value off...
of a quantum mechanical system S. The unitary group generated by i H corresponds to the time evolution of S.
We can also use the Borel functional calculus to abstractly solve some linear initial value problem
Initial value problem
In mathematics, in the field of differential equations, an initial value problem is an ordinary differential equation together with a specified value, called the initial condition, of the unknown function at a given point in the domain of the solution...
s such as the heat equation, or Maxwell's equations.
Existence of a functional calculus
The existence of a mapping with the properties of a functional calculus requires proof. For the case of a bounded self-adjoint operator T, the Borel existence of a Borel functional calculus can be shown in an elementary way as follows:First pass from polynomial to continuous functional calculus
Continuous functional calculus
In mathematics, the continuous functional calculus of operator theory and C*-algebra theory allows applications of continuous functions to normal elements of a C*-algebra. More precisely,Theorem...
by using the Stone-Weierstrass theorem
Stone-Weierstrass theorem
In mathematical analysis, the Weierstrass approximation theorem states that every continuous function defined on an interval [a,b] can be uniformly approximated as closely as desired by a polynomial function...
. The crucial fact here is that, for a bounded self adjoint operator T and a polynomial p,
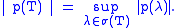
Consequently, the mapping
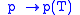
is an isometry and a densely defined homomorphism on the ring of polynomial functions. Extending by continuity defines f(T) for a continuous function f on the spectrum of T. The Riesz-Markov theorem then allows us to pass from integration on continuous functions to spectral measures, and this is the Borel functional calculus.
Alternatively, the continuous calculus can be obtained via the Gelfand transform, in the context of commutative Banach algebras. Extending to measurable functions is achieved by applying Riesz-Markov, as above. In this formulation, T can be a normal operator
Normal operator
In mathematics, especially functional analysis, a normal operator on a complex Hilbert space H is a continuous linear operatorN:H\to Hthat commutes with its hermitian adjoint N*: N\,N^*=N^*N....
.
Given an operator T, the range of the continuous functional calculus h → h(T) is the (abelian) C*-algebra C(T) generated by T. The Borel functional calculus has a larger range, that is the closure of C(T) in the weak operator topology
Weak operator topology
In functional analysis, the weak operator topology, often abbreviated WOT, is the weakest topology on the set of bounded operators on a Hilbert space H, such that the functional sending an operator T to the complex number is continuous for any vectors x and y in the Hilbert space.Equivalently, a...
, a (still abelian) von Neumann algebra
Von Neumann algebra
In mathematics, a von Neumann algebra or W*-algebra is a *-algebra of bounded operators on a Hilbert space that is closed in the weak operator topology and contains the identity operator. They were originally introduced by John von Neumann, motivated by his study of single operators, group...
.
The general functional calculus
We can also define the functional calculus for not necessarily bounded Borel functions h; the result is an operator which in general fails to be bounded. Using the multiplication by a function f model of a self-adjoint operator given by the spectral theorem, this is multiplication by the composition of h with f.Theorem. Let T be a self-adjoint operator on H, h a real-valued Borel function on R. There is a unique operator S such that
The operator S of the previous theorem is denoted h(T).
More generally, a Borel functional calculus also exists for (bounded) normal operators.
Resolution of the identity
Let T be a self-adjoint operator. If E is a Borel subset of R, and 1E is the indicator function of E, then 1E(T) is a self-adjoint projection on H. Then mapping
is a projection-valued measure
Projection-valued measure
In mathematics, particularly functional analysis a projection-valued measure is a function defined on certain subsets of a fixed set and whose values are self-adjoint projections on a Hilbert space...
called the resolution of the identity for the self adjoint operator T. The measure of R with respect to Ω is the identity operator on H. In other words, the identity operator can be expressed as the spectral integral I = ∫ 1 dΩ. Sometimes the term "resolution of the identity" is also used to describe this representation of the identity operator as a spectral integral.
In the case of a discrete measure (in particular, when H is finite dimensional), I = ∫ 1 dΩ can be written as
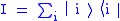
in the Dirac notation, where each |i> is a normalized eigenvector of T. The set { |i⟩ } is an orthonormal basis of H.
In physics literature, using the above as heuristic, one passes to the case when the spectral measure is no longer discrete and write the resolution of identity as
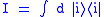
and speak of a "continuous basis", or "continuum of basis states", { |i⟩ }. Mathematically, unless rigorous justifications are given, this expression is purely formal.