
Gluing axiom
Encyclopedia
In mathematics
, the gluing axiom is introduced to define what a sheaf
F on a topological space
X must satisfy, given that it is a presheaf, which is by definition a contravariant functor
to a category C which initially one takes to be the category of sets
. Here O(X) is the partial order of open set
s of X ordered by inclusion map
s; and considered as a category in the standard way, with a unique morphism
if U is a subset
of V, and none otherwise.
As phrased in the sheaf
article, there is a certain axiom that F must satisfy, for any open cover of an open set of X. For example given open sets U and V with union
X and intersection
W, the required condition is that
In less formal language, a section
s of F over X is equally well given by a pair of sections (s′,s′′) on U and V respectively, which 'agree' in the sense that s′ and s′′ have a common image in F(W) under the respective restriction maps
and
The first major hurdle in sheaf theory is to see that this gluing or patching axiom is a correct abstraction from the usual idea in geometric situations. For example, a vector field
is a section of a tangent bundle
on a smooth manifold; this says that a vector field on the union of two open sets is (no more and no less than) vector fields on the two sets that agree where they overlap.
Given this basic understanding, there are further issues in the theory, and some will be addressed here. A different direction is that of the Grothendieck topology
, and yet another is the logical status of 'local existence' (see Kripke–Joyal semantics).
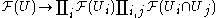
Here the first map is the product of the restriction maps
and each pair of arrows represents the two restrictions
and
It is worthwhile to note that these maps exhaust all of the possible restriction maps among U, the Ui, and the Ui∩Uj.
The condition for F to be a sheaf is exactly that F is the limit
of the diagram. This suggests the correct form of the gluing axiom:
One way of understanding the gluing axiom is to notice that "un-applying" F to (G) yields the following diagram:
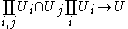
Here U is the colimit of this diagram. The gluing axiom says that F turns colimits of such diagrams into limits.
which satisfies the gluing axiom for sets in O ′(X). We would like to recover the values of F on the other objects of O(X).
To do this, note that for each open set U, we can find a collection {Bj}j∈J whose union is U. Categorically speaking, U is the colimit of the {Bj}j∈J. Since F is contravariant, we define F(U) to be the limit of the {F(B)}j∈J. (Here we must assume that this limit exists in C.) It can be shown that this new object agrees with the old F on each basic open set, and that it is a sheaf.
s; so taking the category C as the category of abelian groups
was only natural. In applications to geometry, for example complex manifold
s and algebraic geometry
, the idea of a sheaf of local ring
s is central. This, however, is not quite the same thing; one speaks instead of a locally ringed space, because it is not true, except in trite cases, that such a sheaf is a functor into a category of local rings. It is the stalks of the sheaf that are local rings, not the collections of sections (which are rings
, but in general are not close to being local). We can think of a locally-ringed space X as a parametrised family of local rings, depending on x in X.
A more careful discussion dispels any mystery here. One can speak freely of a sheaf of abelian groups, or rings, because those are algebraic structure
s (defined, if one insists, by an explicit signature
). Any category C having finite product
s supports the idea of a group object
, which some prefer just to call a group in C. In the case of this kind of purely-algebraic structure, we can talk either of a sheaf having values in the category of abelian groups, or an abelian group in the category of sheaves of sets; it really doesn't matter.
In the local ring case, it does matter. At a foundational level we must use the second style of definition, to describe what a local ring means in a category. This is a logical matter: axioms for a local ring require use of existential quantification
, in the form that for any r in the ring, one of r and 1 − r is invertible. This allows one to specify what a 'local ring in a category' should be, in the case that the category supports enough structure.
This use of language strongly suggests that we are dealing here with adjoint functors
. Therefore it makes sense to observe that the sheaves on X form a full subcategory of the presheaves on X. Implicit in that is the statement that a morphism of sheaves is nothing more than a natural transformation
of the sheaves, considered as functors. Therefore we get an abstract characterisation of sheafification as left adjoint to the inclusion. In some applications, naturally, one does need a description.
In more abstract language, the sheaves on X form a reflective subcategory
of the presheaves (Mac Lane-Moerdijk
Sheaves in Geometry and Logic p. 86). In topos theory, for a Lawvere-Tierney topology and its sheaves, there is an analogous result (ibid. p. 227).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the gluing axiom is introduced to define what a sheaf
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
F on a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X must satisfy, given that it is a presheaf, which is by definition a contravariant functor
- F: O(X) → C
to a category C which initially one takes to be the category of sets
Category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
. Here O(X) is the partial order of open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s of X ordered by inclusion map
Inclusion map
In mathematics, if A is a subset of B, then the inclusion map is the function i that sends each element, x of A to x, treated as an element of B:i: A\rightarrow B, \qquad i=x....
s; and considered as a category in the standard way, with a unique morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
- U → V
if U is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of V, and none otherwise.
As phrased in the sheaf
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
article, there is a certain axiom that F must satisfy, for any open cover of an open set of X. For example given open sets U and V with union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
X and intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
W, the required condition is that
- F(X) is the subset of F(U)×F(V) with equal image in F(W).
In less formal language, a section
Section (category theory)
In category theory, a branch of mathematics, a section is a right inverse of a morphism. Dually, a retraction is a left inverse...
s of F over X is equally well given by a pair of sections (s′,s′′) on U and V respectively, which 'agree' in the sense that s′ and s′′ have a common image in F(W) under the respective restriction maps
- F(U) → F(W)
and
- F(V) → F(W).
The first major hurdle in sheaf theory is to see that this gluing or patching axiom is a correct abstraction from the usual idea in geometric situations. For example, a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
is a section of a tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
on a smooth manifold; this says that a vector field on the union of two open sets is (no more and no less than) vector fields on the two sets that agree where they overlap.
Given this basic understanding, there are further issues in the theory, and some will be addressed here. A different direction is that of the Grothendieck topology
Grothendieck topology
In category theory, a branch of mathematics, a Grothendieck topology is a structure on a category C which makes the objects of C act like the open sets of a topological space. A category together with a choice of Grothendieck topology is called a site.Grothendieck topologies axiomatize the notion...
, and yet another is the logical status of 'local existence' (see Kripke–Joyal semantics).
Removing restrictions on C
To rephrase this definition in a way that will work in any category C that has sufficient structure, we note that we can write the objects and morphisms involved in the definition above in a diagram which we will call (G), for "gluing":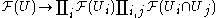
Here the first map is the product of the restriction maps
- resU,Ui,:F(U)→F(Ui)
and each pair of arrows represents the two restrictions
- resUi,Ui∩Uj:F(Ui)→F(Ui∩Uj)
and
- resUj,Ui∩Uj:F(Uj)→F(Ui∩Uj).
It is worthwhile to note that these maps exhaust all of the possible restriction maps among U, the Ui, and the Ui∩Uj.
The condition for F to be a sheaf is exactly that F is the limit
Limit (category theory)
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
of the diagram. This suggests the correct form of the gluing axiom:
- A presheaf F is a sheaf if for any open set U and any collection of open sets {Ui}i∈I whose union is U, F(U) is the limit of the diagram (G) above.
One way of understanding the gluing axiom is to notice that "un-applying" F to (G) yields the following diagram:
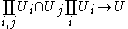
Here U is the colimit of this diagram. The gluing axiom says that F turns colimits of such diagrams into limits.
Sheaves on a basis of open sets
In some categories, it is possible to construct a sheaf by specifying only some of its sections. Specifically, let X be a topological space with basis {Bi}i∈I. We can define a category O ′(X) to be the full subcategory of O(X) whose objects are the {Bi}. A B-sheaf on X with values in C is a contravariant functor- F: O ′(X) → C
which satisfies the gluing axiom for sets in O ′(X). We would like to recover the values of F on the other objects of O(X).
To do this, note that for each open set U, we can find a collection {Bj}j∈J whose union is U. Categorically speaking, U is the colimit of the {Bj}j∈J. Since F is contravariant, we define F(U) to be the limit of the {F(B)}j∈J. (Here we must assume that this limit exists in C.) It can be shown that this new object agrees with the old F on each basic open set, and that it is a sheaf.
The logic of C
The first needs of sheaf theory were for sheaves of abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s; so taking the category C as the category of abelian groups
Category of abelian groups
In mathematics, the category Ab has the abelian groups as objects and group homomorphisms as morphisms. This is the prototype of an abelian category....
was only natural. In applications to geometry, for example complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
s and algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, the idea of a sheaf of local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
s is central. This, however, is not quite the same thing; one speaks instead of a locally ringed space, because it is not true, except in trite cases, that such a sheaf is a functor into a category of local rings. It is the stalks of the sheaf that are local rings, not the collections of sections (which are rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, but in general are not close to being local). We can think of a locally-ringed space X as a parametrised family of local rings, depending on x in X.
A more careful discussion dispels any mystery here. One can speak freely of a sheaf of abelian groups, or rings, because those are algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
s (defined, if one insists, by an explicit signature
Signature (logic)
In logic, especially mathematical logic, a signature lists and describes the non-logical symbols of a formal language. In universal algebra, a signature lists the operations that characterize an algebraic structure. In model theory, signatures are used for both purposes.Signatures play the same...
). Any category C having finite product
Product (category theory)
In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
s supports the idea of a group object
Group object
In category theory, a branch of mathematics, group objects are certain generalizations of groups which are built on more complicated structures than sets...
, which some prefer just to call a group in C. In the case of this kind of purely-algebraic structure, we can talk either of a sheaf having values in the category of abelian groups, or an abelian group in the category of sheaves of sets; it really doesn't matter.
In the local ring case, it does matter. At a foundational level we must use the second style of definition, to describe what a local ring means in a category. This is a logical matter: axioms for a local ring require use of existential quantification
Existential quantification
In predicate logic, an existential quantification is the predication of a property or relation to at least one member of the domain. It is denoted by the logical operator symbol ∃ , which is called the existential quantifier...
, in the form that for any r in the ring, one of r and 1 − r is invertible. This allows one to specify what a 'local ring in a category' should be, in the case that the category supports enough structure.
Sheafification
To turn a given presheaf P into a sheaf F, there is a standard device called sheafification or sheaving. The rough intuition of what one should do, at least for a presheaf of sets, is to introduce an equivalence relation, which makes equivalent data given by different covers on the overlaps by refining the covers. One approach is therefore to go to the stalks and recover the sheaf space of the best possible sheaf F produced from P.This use of language strongly suggests that we are dealing here with adjoint functors
Adjoint functors
In mathematics, adjoint functors are pairs of functors which stand in a particular relationship with one another, called an adjunction. The relationship of adjunction is ubiquitous in mathematics, as it rigorously reflects the intuitive notions of optimization and efficiency...
. Therefore it makes sense to observe that the sheaves on X form a full subcategory of the presheaves on X. Implicit in that is the statement that a morphism of sheaves is nothing more than a natural transformation
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
of the sheaves, considered as functors. Therefore we get an abstract characterisation of sheafification as left adjoint to the inclusion. In some applications, naturally, one does need a description.
In more abstract language, the sheaves on X form a reflective subcategory
Reflective subcategory
In mathematics, a subcategory A of a category B is said to be reflective in B when the inclusion functor from A to B has a left adjoint. This adjoint is sometimes called a reflector...
of the presheaves (Mac Lane-Moerdijk
Ieke Moerdijk
Izak Moerdijk is professor of Mathematics at the Mathematisch Instituut of the Radboud University Nijmegen. He is the author of several influential books.-Selected works:...
Sheaves in Geometry and Logic p. 86). In topos theory, for a Lawvere-Tierney topology and its sheaves, there is an analogous result (ibid. p. 227).

