Algebraic structure
Encyclopedia
In abstract algebra
, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed
under one or more operations
, satisfying some axiom
s. Abstract algebra is primarily the study of algebraic structures and their properties. The notion of algebraic structure
has been formalized in universal algebra
.
In a slight abuse of notation, the expression "structure" can also refer only to the operations on a structure, and not to the underlying set itself. For example, the group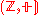
can be seen as a set 
which is equipped with an "algebraic structure", namely the operation 
.
(not to be confused with algebraic variety
in the sense of algebraic geometry
).
Identities are equations formulated using only the operations the structure allows, and variables that are tacitly universally quantified over the relevant universe
. Identities contain no connectives
, existentially quantified variables
, or relations of any kind other than the allowed operations. The study of varieties is an important part of universal algebra
.
An algebraic structure in a variety may be understood as the quotient algebra
of term algebra (also called "absolutely free algebra
") divided by the equivalence relations generated by a set of identities. So, a collection of functions with given signatures
generate a free algebra, the term algebra
T. Given a set of equational identities (the axioms), one may consider their symmetric, transitive closure E. The quotient algebra
T/E is then the algebraic structure or variety. Thus, for example, groups have a signature containing two operators: the multiplication operator m, taking two arguments, and the inverse operator i, taking one argument, and the identity element e, a constant, which may be considered to be an operator taking zero arguments. Given a (countable) set of variables x, y, z, etc. the term algebra is the collection of all possible terms
involving m, i, e and the variables; so for example, m(i(x), m(x,m(y,e))) would be an element of the term algebra. One of the axioms defining a group is the identity m(x, i(x)) = e; another is m(x,e) = x. These equations induce equivalence classes on the free algebra; the quotient algebra then has the algebraic structure of a group.
All structures in this section are elements of naturally defined varieties. Some of these structures are most naturally axiomatized using one or more nonidentities, but are nevertheless varieties because there exists an equivalent axiomatization, one perhaps less perspicuous, composed solely of identities. Algebraic structures that are not varieties are described in the following section, and differ from varieties in their metamathematical
properties.
In this section and the following one, structures are listed in approximate order of increasing complexity, operationalized as follows:
The indentation structure employed in this section and the one following is intended to convey information. If structure B is under structure A and more indented, then all theorem
s of A are theorems of B; the converse does not hold.
Ringoids and lattice
s can be clearly distinguished despite both having two defining binary operations. In the case of ringoids, the two operations are linked by the distributive law; in the case of lattices, they are linked by the absorption law
. Ringoids also tend to have numerical model
s, while lattices tend to have set-theoretic
models.
Simple structures: No binary operation:
Group-like structures:
One binary operation, denoted by concatenation
. For monoid
s, boundary algebra
s, and sloops, S is a pointed set
.
Three binary operations.
Quasigroups are listed here, despite their having 3 binary operations, because they are (nonassociative) magma
s. Quasigroups feature 3 binary operations only because establishing the quasigroup cancellation property
by means of identities alone requires two binary operations in addition to the group operation.
Lattice: Two or more binary operations, including meet and join, connected by the absorption law. S is both a meet and join semilattice, and is a pointed set if and only if S is bounded. Lattices often have no unary operations. Every true statement has a dual
, obtained by replacing every instance of meet with join, and vice versa.
Ringoids: Two binary operations, addition
and multiplication
, with multiplication distributing
over addition. Semirings are pointed sets.
N.B. The above definition of ring does not command universal assent. Some authorities employ "ring" to denote what is here called a rng, and refer to a ring in the above sense as a "ring with identity."
Modules
: Composite Systems Defined over Two Sets, M and R:
The members of:
s, denoted by Greek letters. R is a ring under the binary operations of scalar addition and multiplication; M are module elements (often but not necessarily vectors
), denoted by Latin letters. M is an abelian group
under addition. There may be other binary operations.
The scalar multiplication of scalars and module elements is a function RxM→M which commutes, associates (∀r,s∈R, ∀x∈M, r(sx) = (rs)x ), has 1 as identity element, and distributes over module and scalar addition. If only the pre(post)multiplication of module elements by scalars is defined, the result is a left (right) module.
of the free module. For every v∈M, there exist κ1, ..., κn∈R such that v = κ1e1 + ... + κnen. Let 0 and 0 be the respective identity elements for module and scalar addition. If r1e1 + ... + rnen = 0, then r1 = ... = rn = 0. (Note that the class of free modules over a given ring R is in general not a variety.)
. There is a second binary operation over M, called multiplication and denoted by concatenation, which distributes over module addition and is bilinear: α(xy) = (αx)y = x(αy).
Vector space
s, closely related to modules, are defined in the next section.
Structures whose axioms unavoidably include nonidentities are among the most important ones in mathematics, e.g., field
s and vector space
s. Moreover, much of theoretical physics can be recast as models of multilinear algebra
s. Although structures with nonidentities retain an undoubted algebraic flavor, they suffer from defects varieties do not have. For example, neither the product of integral domains nor a free field over any set exist.
Arithmetics: Two binary operation
s, addition and multiplication. S is an infinite set. Arithmetics are pointed unary systems, whose unary operation
is injective successor, and with distinguished element 0.
Field-like structures: Two binary operations, addition and multiplication. S is nontrivial, i.e., S≠{0}. Division ring
(or sfield, skew field): a ring in which every member of S other than 0 has a two-sided multiplicative inverse. The nonzero members of S form a group
under multiplication.
under multiplication.
The following structures are not varieties for reasons in addition to S≠{0}: Artinian ring
: a ring whose ideals satisfy the descending chain condition.
Composite Systems: Vector Spaces, and Algebras over Fields. Two Sets, M and R, and at least three binary operations.
The members of:
s, denoted by Greek letters. R is a field
, nearly always the real
or complex field, with 0 and 1 as distinguished members.
Three binary operations.
such that ei•ej = 1 if i=j and 0 otherwise; see free module above.Unitary space
: Differs from inner product spaces in that R is the complex field, and the inner product has a different name, the hermitian inner product, with different properties: conjugate symmetric, bilinear, and positive definite. See Birkhoff and Mac Lane (1979: 369).
Graded vector space
: a vector space such that the members of M have a direct sum
decomposition. See graded algebra
below.
Four binary operations. Lie algebra
: an algebra over a field
respecting the Jacobi identity
, whose vector multiplication, the Lie bracket
denoted [ u,v], anticommutes, does not associate, and is nilpotent
. Associative algebra
: an algebra over a field, or a module
, whose vector multiplication associates. M being matrices
. Every matrix has a dimension nxm, n and m positive integers. If one of n or m is 1, the matrix is a vector; if both are 1, it is a scalar. Addition of matrices is defined only if they have the same dimensions. Matrix multiplication
, denoted by concatenation, is the vector multiplication. Let matrix A be nxm and matrix B be ixj. Then AB is defined if and only if m=i; BA, if and only if j=n. There also exists an mxm matrix I and an nxn matrix J such that AI=JA=A. If u and v are vectors having the same dimensions, they have an inner product, denoted 〈u,v〉. Hence there is an orthonormal basis; see inner product space above. There is a unary function, the determinant
, from square (nxn for any n) matrices to R. Commutative algebra
: an associative algebra whose vector multiplication commutes.
Composite Systems: Multilinear algebra
s. Two sets, V and K. Four binary operations:
s (including vectors), denoted by lower case Latin letters. V is an abelian group under multivector addition, and a monoid
under outer product
. The outer product goes under various names, and is multilinear
in principle but usually bilinear. The outer product defines the multivectors recursively starting from the vectors. Thus the members of V have a "degree" (see graded algebra below). Multivectors may have an inner product as well, denoted u•v: V×V→K, that is symmetric, linear
, and positive definite; see inner product space above. The properties and notation of K are the same as those of R above, except that K may have −1 as a distinguished member. K is usually the real field, as multilinear algebras are designed to describe physical phenomena without complex number
s. The multiplication of scalars and multivectors, V×K→V, has the same properties as the multiplication of scalars and module elements that is part of a module.
Geometric algebra
: an exterior algebra whose outer (called geometric) product is denoted by concatenation. The geometric product of parallel multivectors commutes, that of orthogonal vectors anticommutes. The product of a scalar with a multivector commutes. vv yields a scalar.
s; C=complex number
s.
N is a pointed unary system, and under addition and multiplication, is both the standard interpretation of Peano arithmetic and a commutative semiring
.
Boolean algebras are at once semigroup
s, lattices
, and rings
. They would even be abelian group
s if the identity and inverse elements were identical instead of complements.
Group-like structures
(+) is a magma
, and even a free
semigroup
. N under addition is a magma with an identity, and in particular a free monoid
. Z under subtraction
(−) is a quasigroup. Nonzero Q under division
(÷) is a quasigroup. Every group is a loop, because a * x = b if and only if
x = a−1 * b, and y * a = b if and only if y = b * a−1.
2x2 matrices
(of non-zero determinant) with matrix multiplication form a group.
Z under addition (+) is an abelian group.
Nonzero Q under multiplication
(×) is an abelian group.Every cyclic group
G is abelian, because if x, y are in G, then xy = aman = am+n = an+m = anam = yx. In particular, Z is an abelian group under addition, as is the integers modulo n
Z/nZ.A monoid
is a category
with a single object, in which case the composition of morphisms
and the identity morphism interpret monoid multiplication and identity element, respectively.
The Boolean algebra 2 is a boundary algebra.
More examples of groups
and list of small groups.
Lattices
Ring
-like structures
Integral domains
Fields
. The added structure must be compatible, in some sense, with the algebraic structure.
and universal algebra
. Category theory
is another way of reasoning about algebraic structures (see, for example, Mac Lane 1998). A category is a collection of objects with associated morphisms. Every algebraic structure has its own notion of homomorphism
, namely any function
compatible with the operation(s) defining the structure. In this way, every algebraic structure gives rise to a category
. For example, the category of groups
has all groups
as objects and all group homomorphism
s as morphisms. This concrete category
may be seen as a category of sets
with added category-theoretic structure
. Likewise, the category of topological group
s (whose morphisms are the continuous group homomorphisms) is a category of topological spaces
with extra structure. A forgetful functor
between categories of algebraic structures "forgets" a part of a structure.
There are various concepts in category theory that try to capture the algebraic character of a context, for instance
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed
Closure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
under one or more operations
Operation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
, satisfying some axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s. Abstract algebra is primarily the study of algebraic structures and their properties. The notion of algebraic structure
Structure (mathematical logic)
In universal algebra and in model theory, a structure consists of a set along with a collection of finitary operations and relations which are defined on it....
has been formalized in universal algebra
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
.
In a slight abuse of notation, the expression "structure" can also refer only to the operations on a structure, and not to the underlying set itself. For example, the group
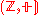can be seen as a set which is equipped with an "algebraic structure", namely the operation .Structures whose axioms are all identities
Universal algebra often considers classes of algebraic structures (such as the class of all groups), together with operations (such as products) and relations (such as "substructure") between these algebras. These classes are usually defined by "axioms", that is, a list of properties that all these structures have to share. If all axioms defining a class of algebras are "identities" , then the corresponding class is called varietyVariety (universal algebra)
In mathematics, specifically universal algebra, a variety of algebras is the class of all algebraic structures of a given signature satisfying a given set of identities. Equivalently, a variety is a class of algebraic structures of the same signature which is closed under the taking of homomorphic...
(not to be confused with algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
in the sense of algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
).
Identities are equations formulated using only the operations the structure allows, and variables that are tacitly universally quantified over the relevant universe
Universe (mathematics)
In mathematics, and particularly in set theory and the foundations of mathematics, a universe is a class that contains all the entities one wishes to consider in a given situation...
. Identities contain no connectives
Logical connective
In logic, a logical connective is a symbol or word used to connect two or more sentences in a grammatically valid way, such that the compound sentence produced has a truth value dependent on the respective truth values of the original sentences.Each logical connective can be expressed as a...
, existentially quantified variables
Quantification
Quantification has several distinct senses. In mathematics and empirical science, it is the act of counting and measuring that maps human sense observations and experiences into members of some set of numbers. Quantification in this sense is fundamental to the scientific method.In logic,...
, or relations of any kind other than the allowed operations. The study of varieties is an important part of universal algebra
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
.
An algebraic structure in a variety may be understood as the quotient algebra
Quotient algebra
In mathematics, a quotient algebra, , also called a factor algebra is obtained by partitioning the elements of an algebra in equivalence classes given by a congruence, that is an equivalence relation that is additionally compatible with all the operations of the algebra, in the formal sense...
of term algebra (also called "absolutely free algebra
Free object
In mathematics, the idea of a free object is one of the basic concepts of abstract algebra. It is a part of universal algebra, in the sense that it relates to all types of algebraic structure . It also has a formulation in terms of category theory, although this is in yet more abstract terms....
") divided by the equivalence relations generated by a set of identities. So, a collection of functions with given signatures
Signature (logic)
In logic, especially mathematical logic, a signature lists and describes the non-logical symbols of a formal language. In universal algebra, a signature lists the operations that characterize an algebraic structure. In model theory, signatures are used for both purposes.Signatures play the same...
generate a free algebra, the term algebra
Term algebra
In universal algebra and mathematical logic, a term algebra is a freely generated algebraic structure over a given signature. For example, in a signature consisting of a single binary operation, the term algebra over a set X of variables is exactly the free magma generated by X...
T. Given a set of equational identities (the axioms), one may consider their symmetric, transitive closure E. The quotient algebra
Quotient algebra
In mathematics, a quotient algebra, , also called a factor algebra is obtained by partitioning the elements of an algebra in equivalence classes given by a congruence, that is an equivalence relation that is additionally compatible with all the operations of the algebra, in the formal sense...
T/E is then the algebraic structure or variety. Thus, for example, groups have a signature containing two operators: the multiplication operator m, taking two arguments, and the inverse operator i, taking one argument, and the identity element e, a constant, which may be considered to be an operator taking zero arguments. Given a (countable) set of variables x, y, z, etc. the term algebra is the collection of all possible terms
Term (mathematics)
A term is a mathematical expression which may form a separable part of an equation, a series, or another expression.-Definition:In elementary mathematics, a term is either a single number or variable, or the product of several numbers or variables separated from another term by a + or - sign in an...
involving m, i, e and the variables; so for example, m(i(x), m(x,m(y,e))) would be an element of the term algebra. One of the axioms defining a group is the identity m(x, i(x)) = e; another is m(x,e) = x. These equations induce equivalence classes on the free algebra; the quotient algebra then has the algebraic structure of a group.
All structures in this section are elements of naturally defined varieties. Some of these structures are most naturally axiomatized using one or more nonidentities, but are nevertheless varieties because there exists an equivalent axiomatization, one perhaps less perspicuous, composed solely of identities. Algebraic structures that are not varieties are described in the following section, and differ from varieties in their metamathematical
Metamathematics
Metamathematics is the study of mathematics itself using mathematical methods. This study produces metatheories, which are mathematical theories about other mathematical theories...
properties.
In this section and the following one, structures are listed in approximate order of increasing complexity, operationalized as follows:
- Simple structures requiring but one set, the universe S, are listed before composite ones requiring two sets;
- Structures having the same number of required sets are then ordered by the number of binary operationBinary operationIn mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
s (0 to 4) they require. Incidentally, no structure mentioned in this entry requires an operation whose arityArityIn logic, mathematics, and computer science, the arity of a function or operation is the number of arguments or operands that the function takes. The arity of a relation is the dimension of the domain in the corresponding Cartesian product...
exceeds 2; - Let A and B be the two sets that make up a composite structure. Then a composite structure may include 1 or 2 functionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s of the form or ; - Structures having the same number and kinds of binary operations and functions are more or less ordered by the number of required unaryUnary operationIn mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
and 0-ary (distinguished elements) operations, 0 to 2 in both cases.
The indentation structure employed in this section and the one following is intended to convey information. If structure B is under structure A and more indented, then all theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
s of A are theorems of B; the converse does not hold.
Ringoids and lattice
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
s can be clearly distinguished despite both having two defining binary operations. In the case of ringoids, the two operations are linked by the distributive law; in the case of lattices, they are linked by the absorption law
Absorption law
In algebra, the absorption law or absorption identity is an identity linking a pair of binary operations.Two binary operations, say ¤ and *, are said to be connected by the absorption law if:...
. Ringoids also tend to have numerical model
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
s, while lattices tend to have set-theoretic
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
models.
Simple structures: No binary operation:
- Set: a degenerate algebraic structure having no operations.
- Pointed setPointed setIn mathematics, a pointed set is a set X with a distinguished element x_0\in X, which is called the basepoint. Maps of pointed sets are those functions that map one basepoint to another, i.e. a map f : X \to Y such that f = y_0. This is usually denotedf : \to .Pointed sets may be regarded as a...
: S has one or more distinguished elements, often 0, 1, or both. - Unary system: S and a single unary operation over S.
- Pointed unary system: a unary system with S a pointed set.
Group-like structures:
One binary operation, denoted by concatenation
Concatenation
In computer programming, string concatenation is the operation of joining two character strings end-to-end. For example, the strings "snow" and "ball" may be concatenated to give "snowball"...
. For monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
s, boundary algebra
Laws of Form
Laws of Form is a book by G. Spencer-Brown, published in 1969, that straddles the boundary between mathematics and philosophy...
s, and sloops, S is a pointed set
Pointed set
In mathematics, a pointed set is a set X with a distinguished element x_0\in X, which is called the basepoint. Maps of pointed sets are those functions that map one basepoint to another, i.e. a map f : X \to Y such that f = y_0. This is usually denotedf : \to .Pointed sets may be regarded as a...
.
- Magma or groupoidMagma (algebra)In abstract algebra, a magma is a basic kind of algebraic structure. Specifically, a magma consists of a set M equipped with a single binary operation M \times M \rightarrow M....
: S and a single binary operation over S.- Steiner magma: A commutative magma satisfying x(xy) = y.
- Squag: an idempotent Steiner magma.
- Sloop: a Steiner magma with distinguished element 1, such that xx = 1.
- Steiner magma: A commutative magma satisfying x(xy) = y.
- SemigroupSemigroupIn mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
: an associative magma.- MonoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
: a unital semigroup.- GroupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
: a monoid with a unary operation, inverse, giving rise to an inverse elementInverse elementIn abstract algebra, the idea of an inverse element generalises the concept of a negation, in relation to addition, and a reciprocal, in relation to multiplication. The intuition is of an element that can 'undo' the effect of combination with another given element...
.- Abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
: a commutative group.
- Abelian group
- Group
- BandBand (algebra)In mathematics, a band is a semigroup in which every element is idempotent . Bands were first studied and named by ; the lattice of varieties of bands was described independently in the early 1970s by Biryukov, Fennemore and Gerhard...
: a semigroup of idempotents.- SemilatticeSemilatticeIn mathematics, a join-semilattice is a partially ordered set which has a join for any nonempty finite subset. Dually, a meet-semilattice is a partially ordered set which has a meet for any nonempty finite subset...
: a commutative band. The binary operation can be called either meetMeet (mathematics)In mathematics, join and meet are dual binary operations on the elements of a partially ordered set. A join on a set is defined as the supremum with respect to a partial order on the set, provided a supremum exists...
or join.- Boundary algebra: a unital semilattice (equivalently, an idempotent commutative monoid) with a unary operation, complementationComplemented latticeIn the mathematical discipline of order theory, a complemented lattice is a bounded lattice in which every element a has a complement, i.e. an element b satisfying a ∨ b = 1 and a ∧ b = 0....
, denoted by enclosing its argument in parentheses, giving rise to an inverse element that is the complement of the identity elementIdentity elementIn mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
. The identity and inverse elements bound S. Also, x(xy) = x(y) holds.
- Boundary algebra: a unital semilattice (equivalently, an idempotent commutative monoid) with a unary operation, complementation
- Semilattice
- Monoid
Three binary operations.
Quasigroups are listed here, despite their having 3 binary operations, because they are (nonassociative) magma
Magma (algebra)
In abstract algebra, a magma is a basic kind of algebraic structure. Specifically, a magma consists of a set M equipped with a single binary operation M \times M \rightarrow M....
s. Quasigroups feature 3 binary operations only because establishing the quasigroup cancellation property
Cancellation property
In mathematics, the notion of cancellative is a generalization of the notion of invertible.An element a in a magma has the left cancellation property if for all b and c in M, a * b = a * c always implies b = c.An element a in a magma has the right cancellation...
by means of identities alone requires two binary operations in addition to the group operation.
- QuasigroupQuasigroupIn mathematics, especially in abstract algebra, a quasigroup is an algebraic structure resembling a group in the sense that "division" is always possible...
: a cancellative magma. Equivalently, ∀x,y∈S, ∃!a,b∈S, such that xa = y and bx = y.- Loop: a unital quasigroup with a unary operation, inverse.
- Moufang loopMoufang loopIn mathematics, a Moufang loop is a special kind of algebraic structure. It is similar to a group in many ways but need not be associative. Moufang loops were introduced by Ruth Moufang.-Definition:...
: a loop in which a weakened form of associativity, (zx)(yz) = z(xy)z, holds.- Group: an associative loop.
- Moufang loop
- Loop: a unital quasigroup with a unary operation, inverse.
Lattice: Two or more binary operations, including meet and join, connected by the absorption law. S is both a meet and join semilattice, and is a pointed set if and only if S is bounded. Lattices often have no unary operations. Every true statement has a dual
Duality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
, obtained by replacing every instance of meet with join, and vice versa.
- Bounded lattice: S has two distinguished elements, the greatest lower bound and the least upper bound. Dualizing requires replacing every instance of one bound by the other, and vice versa.
- Complemented latticeComplemented latticeIn the mathematical discipline of order theory, a complemented lattice is a bounded lattice in which every element a has a complement, i.e. an element b satisfying a ∨ b = 1 and a ∧ b = 0....
: a lattice with a unary operation, complementation, denoted by postfixReverse Polish notationReverse Polish notation is a mathematical notation wherein every operator follows all of its operands, in contrast to Polish notation, which puts the operator in the prefix position. It is also known as Postfix notation and is parenthesis-free as long as operator arities are fixed...
" ' ", giving rise to an inverse element. That element and its complement bound the lattice.
- Complemented lattice
- Modular latticeModular latticeIn the branch of mathematics called order theory, a modular lattice is a lattice that satisfies the following self-dual condition:Modular law: x ≤ b implies x ∨ = ∧ b,where ≤ is the partial order, and ∨ and ∧ are...
: a lattice in which the modular identity holds.- Distributive latticeDistributive latticeIn mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...
: a lattice in which each of meet and join distributesDistributive latticeIn mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...
over the other. Distributive lattices are modular, but the converse does not hold.- Kleene algebraKleene algebraIn mathematics, a Kleene algebra is either of two different things:* A bounded distributive lattice with an involution satisfying De Morgan's laws , additionally satisfying the inequality x∧−x ≤ y∨−y. Kleene algebras are subclasses of Ockham algebras...
: a bounded distributive lattice with a unary operation whose identities are x"=x, (x+y)'=x'y', and (x+x')yy'=yy'. See "ring-like structures" for another structure having the same name. - Boolean algebra: a complemented distributive lattice. Either of meet or join can be defined in terms of the other and complementation.
- Interior algebraInterior algebraIn abstract algebra, an interior algebra is a certain type of algebraic structure that encodes the idea of the topological interior of a set. Interior algebras are to topology and the modal logic S4 what Boolean algebras are to set theory and ordinary propositional logic...
: a Boolean algebra with an added unary operation, the interior operator, denoted by postfix " ' " and obeying the identities x'x=x, x"=x, (xy)'=x'y', and 1'=1.
- Interior algebra
- Heyting algebraHeyting algebraIn mathematics, a Heyting algebra, named after Arend Heyting, is a bounded lattice equipped with a binary operation a→b of implication such that ∧a ≤ b, and moreover a→b is the greatest such in the sense that if c∧a ≤ b then c ≤ a→b...
: a bounded distributive lattice with an added binary operation, relative pseudo-complement, denoted by infixInfixAn infix is an affix inserted inside a word stem . It contrasts with adfix, a rare term for an affix attached to the end of a stem, such as a prefix or suffix.-Indonesian:...
" ' ", and governed by the axioms x'x=1, x(x'y) = xy, x'(yz) = (x'y)(x'z), (xy)'z = (x'z)(y'z).
- Kleene algebra
- Distributive lattice
Ringoids: Two binary operations, addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
and multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
, with multiplication distributing
Distributivity
In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
over addition. Semirings are pointed sets.
- SemiringSemiringIn abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse...
: a ringoid such that S is a monoid under each operation. Each operation has a distinct identity element. Addition also commutes, and has an identity element that annihilates multiplication.- Commutative semiring: a semiring with commutative multiplication.
- RingRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
: a semiring with a unary operation, additive inverse, giving rise to an inverse element -x, which when added to x, yields the additive identity element. Hence S is an abelian group under addition.- RngRng (algebra)In abstract algebra, a rng is an algebraic structure satisfying the same properties as a ring, except that multiplication need not have an identity element...
: a ring lacking a multiplicative identity. - Commutative ringCommutative ringIn ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
: a ring with commutative multiplication.- Boolean ringBoolean ringIn mathematics, a Boolean ring R is a ring for which x2 = x for all x in R; that is, R consists only of idempotent elements....
: a commutative ring with idempotent multiplication, equivalent to a Boolean algebra.
- Boolean ring
- Rng
- Kleene algebra: a semiring with idempotent addition and a unary operation, the Kleene starKleene starIn mathematical logic and computer science, the Kleene star is a unary operation, either on sets of strings or on sets of symbols or characters. The application of the Kleene star to a set V is written as V*...
, denoted by postfix * and obeying the identities (1+x*x)x*=x* and (1+xx*)x*=x*. See "Lattice-like structures" for another structure having the same name.
N.B. The above definition of ring does not command universal assent. Some authorities employ "ring" to denote what is here called a rng, and refer to a ring in the above sense as a "ring with identity."
Modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
: Composite Systems Defined over Two Sets, M and R:
The members of:
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
s, denoted by Greek letters. R is a ring under the binary operations of scalar addition and multiplication; M are module elements (often but not necessarily vectors
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
), denoted by Latin letters. M is an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
under addition. There may be other binary operations.
The scalar multiplication of scalars and module elements is a function RxM→M which commutes, associates (∀r,s∈R, ∀x∈M, r(sx) = (rs)x ), has 1 as identity element, and distributes over module and scalar addition. If only the pre(post)multiplication of module elements by scalars is defined, the result is a left (right) module.
- Free moduleFree moduleIn mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
: a module having a free basisBasis (linear algebra)In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
, {
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
of the free module. For every v∈M, there exist κ1, ..., κn∈R such that v = κ1e1 + ... + κnen. Let 0 and 0 be the respective identity elements for module and scalar addition. If r1e1 + ... + rnen = 0, then r1 = ... = rn = 0. (Note that the class of free modules over a given ring R is in general not a variety.)
- Algebra over a ring (also
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
. There is a second binary operation over M, called multiplication and denoted by concatenation, which distributes over module addition and is bilinear: α(xy) = (αx)y = x(αy).
- Jordan ringJordan algebraIn abstract algebra, a Jordan algebra is an algebra over a field whose multiplication satisfies the following axioms:# xy = yx # = x ....
: an algebra over a ring whose module multiplication commutes, does not associate, and respects the Jordan identity.
Vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s, closely related to modules, are defined in the next section.
Structures with some axioms that are not identities
The structures in this section are not axiomatized with identities alone, so the classes considered below are not varieties. Nearly all of the nonidentities below are one of two very elementary kinds:- The starting point for all structures in this section is a "nontrivial" ring, namely one such that S≠{0}, 0 being the additive identity elementIdentity elementIn mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
. The nearest thing to an identity implying S≠{0} is the nonidentity 0≠1, which requires that the additive and multiplicative identities be distinct. - Nearly all structures described in this section include identities that hold for all members of S except 0. In order for an algebraic structure to be a variety, its operations must be defined for all members of S; there can be no partial operations.
Structures whose axioms unavoidably include nonidentities are among the most important ones in mathematics, e.g., field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
s and vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s. Moreover, much of theoretical physics can be recast as models of multilinear algebra
Multilinear algebra
In mathematics, multilinear algebra extends the methods of linear algebra. Just as linear algebra is built on the concept of a vector and develops the theory of vector spaces, multilinear algebra builds on the concepts of p-vectors and multivectors with Grassmann algebra.-Origin:In a vector space...
s. Although structures with nonidentities retain an undoubted algebraic flavor, they suffer from defects varieties do not have. For example, neither the product of integral domains nor a free field over any set exist.
Arithmetics: Two binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
s, addition and multiplication. S is an infinite set. Arithmetics are pointed unary systems, whose unary operation
Unary operation
In mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
is injective successor, and with distinguished element 0.
- Robinson arithmeticRobinson arithmeticIn mathematics, Robinson arithmetic, or Q, is a finitely axiomatized fragment of Peano arithmetic , first set out in R. M. Robinson . Q is essentially PA without the axiom schema of induction. Since Q is weaker than PA, it is incomplete...
. Addition and multiplication are recursivelyRecursionRecursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
defined by means of successor. 0 is the identity element for addition, and annihilates multiplication. Robinson arithmetic is listed here even though it is a variety, because of its closeness to Peano arithmetic.- Peano arithmetic. Robinson arithmetic with an axiom schemaAxiom schemaIn mathematical logic, an axiom schema generalizes the notion of axiom.An axiom schema is a formula in the language of an axiomatic system, in which one or more schematic variables appear. These variables, which are metalinguistic constructs, stand for any term or subformula of the system, which...
of inductionMathematical inductionMathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
. Most ring and field axioms bearing on the properties of addition and multiplication are theorems of Peano arithmetic or of proper extensions thereof.
- Peano arithmetic. Robinson arithmetic with an axiom schema
Field-like structures: Two binary operations, addition and multiplication. S is nontrivial, i.e., S≠{0}.
- DomainDomain (ring theory)In mathematics, especially in the area of abstract algebra known as ring theory, a domain is a ring such that ab = 0 implies that either a = 0 or b = 0. That is, it is a ring which has no left or right zero divisors. Some authors require the ring to be nontrivial...
: a ring whose sole zero divisorZero divisorIn abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
is 0.- Integral domain: a domain whose multiplication commutes. Also a commutative cancellative ring.
- Euclidean domainEuclidean domainIn mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm...
: an integral domain with a function
- Euclidean domain
- Integral domain: a domain whose multiplication commutes. Also a commutative cancellative ring.
Division ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
(or sfield, skew field): a ring in which every member of S other than 0 has a two-sided multiplicative inverse. The nonzero members of S form a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
under multiplication.
- Field: a division ring whose multiplication commutes. The nonzero members of
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
under multiplication.
- Ordered fieldOrdered fieldIn mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
: a field whose elements are totally ordered.- Real fieldFormally real fieldIn mathematics, in particular in field theory and real algebra, a formally real field is a field that admits an ordering which makes it an ordered field.-Alternative Definitions:...
: a Dedekind complete ordered field.
- Real field
The following structures are not varieties for reasons in addition to S≠{0}:
- Simple ringSimple ringIn abstract algebra, a simple ring is a non-zero ring that has no ideal besides the zero ideal and itself. A simple ring can always be considered as a simple algebra. This notion must not be confused with the related one of a ring being simple as a left module over itself...
: a ring having no idealsIdeal (ring theory)In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
other than 0 and
Artinian ring
In abstract algebra, an Artinian ring is a ring that satisfies the descending chain condition on ideals. They are also called Artin rings and are named after Emil Artin, who first discovered that the descending chain condition for ideals simultaneously generalizes finite rings and rings that are...
: a ring whose ideals satisfy the descending chain condition.
Composite Systems: Vector Spaces, and Algebras over Fields. Two Sets, M and R, and at least three binary operations.
The members of:
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
s, denoted by Greek letters. R is a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, nearly always the real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex field, with 0 and 1 as distinguished members.
Three binary operations.
- Vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
: a free moduleFree moduleIn mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
of dimensionDimensionIn physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
- Normed vector spaceNormed vector spaceIn mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
: a vector space and with a normNorm (mathematics)In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
, namely a function
- Inner product spaceInner product spaceIn mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
(also
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
such that ei•ej = 1 if i=j and 0 otherwise; see free module above.
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
: Differs from inner product spaces in that
Graded vector space
In mathematics, a graded vector space is a type of vector space that includes the extra structure of gradation, which is a decomposition of the vector space into a direct sum of vector subspaces.-N-graded vector spaces:...
: a vector space such that the members of
Direct sum of modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
decomposition. See graded algebra
Graded algebra
In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....
below.
Four binary operations.
- Algebra over a fieldAlgebra over a fieldIn mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
: An algebra over a ring except that
- Jordan algebraJordan algebraIn abstract algebra, a Jordan algebra is an algebra over a field whose multiplication satisfies the following axioms:# xy = yx # = x ....
: a Jordan ring except that
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
: an algebra over a field
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
respecting the Jacobi identity
Jacobi identity
In mathematics the Jacobi identity is a property that a binary operation can satisfy which determines how the order of evaluation behaves for the given operation. Unlike for associative operations, order of evaluation is significant for operations satisfying Jacobi identity...
, whose vector multiplication, the Lie bracket
Lie bracket of vector fields
In the mathematical field of differential topology, the Lie bracket of vector fields, Jacobi–Lie bracket, or commutator of vector fields is a bilinear differential operator which assigns, to any two vector fields X and Y on a smooth manifold M, a third vector field denoted [X, Y]...
denoted [
Nilpotent
In mathematics, an element x of a ring R is called nilpotent if there exists some positive integer n such that xn = 0....
.
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
: an algebra over a field, or a module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
, whose vector multiplication associates.
- Linear algebraLinear algebraLinear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
: an associative unital algebra with the members of
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. Every matrix has a dimension nxm, n and m positive integers. If one of n or m is 1, the matrix is a vector; if both are 1, it is a scalar. Addition of matrices is defined only if they have the same dimensions. Matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
, denoted by concatenation, is the vector multiplication. Let matrix A be nxm and matrix B be ixj. Then AB is defined if and only if m=i; BA, if and only if j=n. There also exists an mxm matrix I and an nxn matrix J such that AI=JA=A. If u and v are vectors having the same dimensions, they have an inner product, denoted 〈u,v〉. Hence there is an orthonormal basis; see inner product space above. There is a unary function, the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
, from square (nxn for any n) matrices to R.
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
: an associative algebra whose vector multiplication commutes.
- Symmetric algebraSymmetric algebraIn mathematics, the symmetric algebra S on a vector space V over a field K is the free commutative unital associative algebra over K containing V....
: a commutative algebra with unital vector multiplication.
Composite Systems: Multilinear algebra
Multilinear algebra
In mathematics, multilinear algebra extends the methods of linear algebra. Just as linear algebra is built on the concept of a vector and develops the theory of vector spaces, multilinear algebra builds on the concepts of p-vectors and multivectors with Grassmann algebra.-Origin:In a vector space...
s. Two sets, V and K. Four binary operations:
- The members of
Multivector
In multilinear algebra, a multivector or clif is an element of the exterior algebra on a vector space, \Lambda^* V. This algebra consists of linear combinations of simple k-vectors v_1\wedge\cdots\wedge v_k."Multivector" may mean either homogeneous elements In multilinear algebra, a multivector...
s (including vectors), denoted by lower case Latin letters. V is an abelian group under multivector addition, and a monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
under outer product
Outer product
In linear algebra, the outer product typically refers to the tensor product of two vectors. The result of applying the outer product to a pair of vectors is a matrix...
. The outer product goes under various names, and is multilinear
Tensor (intrinsic definition)
In mathematics, the modern component-free approach to the theory of a tensor views a tensor as an abstract object, expressing some definite type of multi-linear concept...
in principle but usually bilinear. The outer product defines the multivectors recursively starting from the vectors. Thus the members of V have a "degree" (see graded algebra below). Multivectors may have an inner product as well, denoted u•v: V×V→K, that is symmetric, linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
, and positive definite; see inner product space above.
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s.
- Graded algebraGraded algebraIn mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....
: an associative algebra with unital outer product. The members of
- Exterior algebraExterior algebraIn mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
(also
- Clifford algebraClifford algebraIn mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
: an exterior algebra with a symmetric bilinear form
Geometric algebra
Geometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
: an exterior algebra whose outer (called
- Grassmann-Cayley algebraGrassmann-Cayley algebraGrassmann–Cayley algebra, also known as double algebra, is a form of modeling algebra for use in projective geometry. The technique is based on work by German mathematician Hermann Grassmann on exterior algebra, and subsequently by British mathematician Arthur Cayley's work on matrices and linear...
: a geometric algebra without an inner product.
Examples
Some recurring universes: N=natural numbers; Z=integers; Q=rational numbers; R=real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s; C=complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s.
N is a pointed unary system, and under addition and multiplication, is both the standard interpretation of Peano arithmetic and a commutative semiring
Semiring
In abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse...
.
Boolean algebras are at once semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
s, lattices
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
, and rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
. They would even be abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s if the identity and inverse elements were identical instead of complements.
Group-like structures
- Nonzero
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
(+) is a magma
Magma (algebra)
In abstract algebra, a magma is a basic kind of algebraic structure. Specifically, a magma consists of a set M equipped with a single binary operation M \times M \rightarrow M....
, and even a free
Free semigroup
In abstract algebra, the free monoid on a set A is the monoid whose elements are all the finite sequences of zero or more elements from A. It is usually denoted A∗. The identity element is the unique sequence of zero elements, often called the empty string and denoted by ε or λ, and the...
semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
. N under addition is a magma with an identity, and in particular a free monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
.
Subtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
(−) is a quasigroup.
Division (mathematics)
right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
(÷) is a quasigroup.
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
x = a−1 * b, and y * a = b if and only if y = b * a−1.
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
(of non-zero determinant) with matrix multiplication form a group.
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
(×) is an abelian group.
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
G is abelian, because if x, y are in G, then xy = aman = am+n = an+m = anam = yx. In particular,
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
Z/nZ.
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
is a category
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
with a single object, in which case the composition of morphisms
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
and the identity morphism interpret monoid multiplication and identity element, respectively.
Examples of groups
Some elementary examples of groups in mathematics are given on Group .Further examples are listed here.-Permutations of a set of three elements:Consider three colored blocks , initially placed in the order RGB...
and list of small groups.
Lattices
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
- The normal subgroupNormal subgroupIn abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
s of a group, and the submodules of a module, are modular lattices. - Any field of sets, and the connectivesLogical connectiveIn logic, a logical connective is a symbol or word used to connect two or more sentences in a grammatically valid way, such that the compound sentence produced has a truth value dependent on the respective truth values of the original sentences.Each logical connective can be expressed as a...
of first-order logicFirst-order logicFirst-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
, are models of Boolean algebra. - The connectives of intuitionistic logicIntuitionistic logicIntuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
form a model of Heyting algebraHeyting algebraIn mathematics, a Heyting algebra, named after Arend Heyting, is a bounded lattice equipped with a binary operation a→b of implication such that ∧a ≤ b, and moreover a→b is the greatest such in the sense that if c∧a ≤ b then c ≤ a→b...
. - The modal logicModal logicModal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
S4 is a model of interior algebraInterior algebraIn abstract algebra, an interior algebra is a certain type of algebraic structure that encodes the idea of the topological interior of a set. Interior algebras are to topology and the modal logic S4 what Boolean algebras are to set theory and ordinary propositional logic...
. - Peano arithmetic and most axiomatic set theories, including ZFC, NBGVon Neumann–Bernays–Gödel set theoryIn the foundations of mathematics, von Neumann–Bernays–Gödel set theory is an axiomatic set theory that is a conservative extension of the canonical axiomatic set theory ZFC. A statement in the language of ZFC is provable in NBG if and only if it is provable in ZFC. The ontology of NBG includes...
, and New foundationsNew FoundationsIn mathematical logic, New Foundations is an axiomatic set theory, conceived by Willard Van Orman Quine as a simplification of the theory of types of Principia Mathematica. Quine first proposed NF in a 1937 article titled "New Foundations for Mathematical Logic"; hence the name...
, can be recast as models of relation algebraRelation algebraIn mathematics and abstract algebra, a relation algebra is a residuated Boolean algebra expanded with an involution called converse, a unary operation...
.
Ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
-like structures
- The set R[X] of all polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s over some coefficient ring R is a ring. - 2x2 matrices with matrix addition and multiplication form a ring.
- If n is a positive integer, then the set Zn = Z/nZ of integers modulo n (the additive cyclic group of order n ) forms a ring having n elements (see modular arithmetic).
- Sets of hypercomplex numberHypercomplex numberIn mathematics, a hypercomplex number is a traditional term for an element of an algebra over a field where the field is the real numbers or the complex numbers. In the nineteenth century number systems called quaternions, tessarines, coquaternions, biquaternions, and octonions became established...
s were early prototypes of algebraic structures now called rings.
Integral domains
- Z under addition and multiplication is an integral domain.
- The p-adic integersP-adic numberIn mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
.
Fields
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
- Each of Q, R, and C, under addition and multiplication, is a field.
- R totally ordered by "<" in the usual way is an ordered fieldOrdered fieldIn mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
and is categoricalCategoricalSee:* Categorical imperative* Morley's categoricity theorem* Categorical data analysis* Categorical distribution* Categorical logic* Categorical syllogism* Categorical proposition* Categorization* Categorical perception* Category theory...
. The resulting real field grounds realReal analysisReal analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
and functional analysisFunctional analysisFunctional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
.- R contains several interesting subfields, the algebraicAlgebraic numberIn mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
, the computableComputable numberIn mathematics, particularly theoretical computer science and mathematical logic, the computable numbers, also known as the recursive numbers or the computable reals, are the real numbers that can be computed to within any desired precision by a finite, terminating algorithm...
, and the definable numberDefinable numberA real number a is first-order definable in the language of set theory, without parameters, if there is a formula φ in the language of set theory, with one free variable, such that a is the unique real number such that φ holds in the standard model of set theory .For the purposes of this article,...
s.
- R contains several interesting subfields, the algebraic
- An algebraic number fieldAlgebraic number fieldIn mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
is a finite field extensionField extensionIn abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
of Q, that is, a field containing Q which has finite dimension as a vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over Q. Algebraic number fields are very important in number theoryNumber theoryNumber theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
. - If q > 1 is a power of a prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
, then there exists (up toUp toIn mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
isomorphismIsomorphismIn abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
) exactly one finite fieldFinite fieldIn abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
with q elements, usually denoted Fq, or in the case that q is itself prime, by Z/qZ. Such fields are called Galois fields, whence the alternative notation GF(q). All finite fields are isomorphic to some Galois field.- Given some prime number
Allowing additional structure
Algebraic structures can also be defined on sets with added structure of a non-algebraic nature, such as a topologyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
. The added structure must be compatible, in some sense, with the algebraic structure.
- Ordered groupOrdered groupIn abstract algebra, a partially-ordered group is a group equipped with a partial order "≤" that is translation-invariant; in other words, "≤" has the property that, for all a, b, and g in G, if a ≤ b then a+g ≤ b+g and g+a ≤ g+b.An element x of G is called positive element if 0 ≤ x...
: a group with a compatible partial order. I.e., S is partially ordered. - Linearly ordered groupLinearly ordered groupIn abstract algebra a linearly ordered or totally ordered group is an ordered group G such that the order relation "≤" is total...
: a group whose S is a linear order. - Archimedean groupArchimedean groupIn abstract algebra, a branch of mathematics, an Archimedean group is an algebraic structure consisting of a set together with a binary operation and binary relation satisfying certain axioms detailed below. We can also say that an Archimedean group is a linearly ordered group for which the...
: a linearly ordered group for which the Archimedean propertyArchimedean propertyIn abstract algebra and analysis, the Archimedean property, named after the ancient Greek mathematician Archimedes of Syracuse, is a property held by some ordered or normed groups, fields, and other algebraic structures. Roughly speaking, it is the property of having no infinitely large or...
holds. - Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
: a group whose S has a compatible smooth manifoldManifoldIn mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
structure. - Topological groupTopological groupIn mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
: a group whose S has a compatible topology. - Topological vector spaceTopological vector spaceIn mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
: a vector space whose M has a compatible topology; a superset of normed vector spaceNormed vector spaceIn mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
s. - Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s, Hilbert spaces, Inner product spaceInner product spaceIn mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
s - Vertex operator algebraVertex operator algebraIn mathematics, a vertex operator algebra is an algebraic structure that plays an important role in conformal field theory and related areas of physics...
s
Category theory
The discussion above has been cast in terms of elementary abstractAbstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
and universal algebra
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
. Category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
is another way of reasoning about algebraic structures (see, for example, Mac Lane 1998). A category is a collection of objects with associated morphisms. Every algebraic structure has its own notion of homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
, namely any function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
compatible with the operation(s) defining the structure. In this way, every algebraic structure gives rise to a category
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
. For example, the category of groups
Category of groups
In mathematics, the category Grp has the class of all groups for objects and group homomorphisms for morphisms. As such, it is a concrete category...
has all groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
as objects and all group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
s as morphisms. This concrete category
Concrete category
In mathematics, a concrete category is a category that is equipped with a faithful functor to the category of sets. This functor makes it possible to think of the objects of the category as sets with additional structure, and of its morphisms as structure-preserving functions...
may be seen as a category of sets
Category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
with added category-theoretic structure
Structure (category theory)
In mathematics, progress often consists of recognising the same structure in different contexts - so that one method exploiting it has multiple applications...
. Likewise, the category of topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
s (whose morphisms are the continuous group homomorphisms) is a category of topological spaces
Category of topological spaces
In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
with extra structure. A forgetful functor
Forgetful functor
In mathematics, in the area of category theory, a forgetful functor is a type of functor. The nomenclature is suggestive of such a functor's behaviour: given some object with structure as input, some or all of the object's structure or properties is 'forgotten' in the output...
between categories of algebraic structures "forgets" a part of a structure.
There are various concepts in category theory that try to capture the algebraic character of a context, for instance
- algebraic
- essentially algebraic
- presentable
- locally presentable
- monadicMonad (category theory)In category theory, a branch of mathematics, a monad, Kleisli triple, or triple is an functor, together with two natural transformations...
functors and categories - universal propertyUniversal propertyIn various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
.
See also
- free objectFree objectIn mathematics, the idea of a free object is one of the basic concepts of abstract algebra. It is a part of universal algebra, in the sense that it relates to all types of algebraic structure . It also has a formulation in terms of category theory, although this is in yet more abstract terms....
- list of algebraic structures
- list of first order theories
- signatureSignature (logic)In logic, especially mathematical logic, a signature lists and describes the non-logical symbols of a formal language. In universal algebra, a signature lists the operations that characterize an algebraic structure. In model theory, signatures are used for both purposes.Signatures play the same...
External links
- Jipsen's algebra structures. Includes many structures not mentioned here.
- Mathworld page on abstract algebra.
- Stanford Encyclopedia of PhilosophyStanford Encyclopedia of PhilosophyThe Stanford Encyclopedia of Philosophy is a freely-accessible online encyclopedia of philosophy maintained by Stanford University. Each entry is written and maintained by an expert in the field, including professors from over 65 academic institutions worldwide...
: Algebra by Vaughan Pratt.