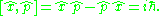Momentum operator
Encyclopedia
In quantum mechanics
, momentum is defined as an operator
on the wave function. The Heisenberg
uncertainty principle
defines limits on how accurately the momentum and position of a single observable system can be known at once. In quantum mechanics, position
and momentum are conjugate variables.
For a single particle with no electric charge
and no spin
, the momentum operator can be written in the position basis as

where:
In one space dimension this becomes:
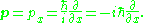
This is a commonly encountered form of the momentum operator, though not the most general one.
The momentum operator is always a Hermitian operator when it acts on physical (in particular, normalizable) quantum states.
of the momentum in quantum mechanics
is the position operator. The Fourier transform turns the momentum-basis into the position-basis.
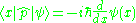
The same applies for the Position operator
in the momentum basis:
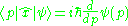
and other useful relations:

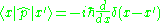
where stands for Dirac's delta function.
stands for Dirac's delta function.
 , where
, where  represents the length of the infinitesimal translation, then
represents the length of the infinitesimal translation, then
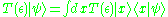
that becomes
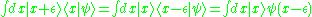
We assume the function to be analytic
to be analytic
(or simply differentiable, for simplicity), so we may write: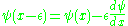
so we have for infinitesimal
values of epsilon:
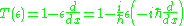
we know from classical mechanics
that momentum
is the generator of translation
, so we know that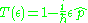
thus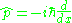
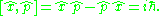
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, momentum is defined as an operator
Operator (physics)
In physics, an operator is a function acting on the space of physical states. As a resultof its application on a physical state, another physical state is obtained, very often along withsome extra relevant information....
on the wave function. The Heisenberg
Werner Heisenberg
Werner Karl Heisenberg was a German theoretical physicist who made foundational contributions to quantum mechanics and is best known for asserting the uncertainty principle of quantum theory...
uncertainty principle
Uncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
defines limits on how accurately the momentum and position of a single observable system can be known at once. In quantum mechanics, position
Position operator
In quantum mechanics, the position operator is the operator that corresponds to the position observable of a particle. Consider, for example, the case of a spinless particle moving on a line. The state space for such a particle is L2, the Hilbert space of complex-valued and square-integrable ...
and momentum are conjugate variables.
For a single particle with no electric charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
and no spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
, the momentum operator can be written in the position basis as

where:
-
 is the gradientGradientIn vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
is the gradientGradientIn vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
operator; -
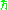 is the reduced Planck constant;
is the reduced Planck constant; -
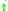 is the imaginary unitImaginary unitIn mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
is the imaginary unitImaginary unitIn mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
.
In one space dimension this becomes:
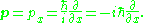
This is a commonly encountered form of the momentum operator, though not the most general one.
The momentum operator is always a Hermitian operator when it acts on physical (in particular, normalizable) quantum states.
Fourier transform
One can show that the Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of the momentum in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
is the position operator. The Fourier transform turns the momentum-basis into the position-basis.
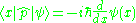
The same applies for the Position operator
Position operator
In quantum mechanics, the position operator is the operator that corresponds to the position observable of a particle. Consider, for example, the case of a spinless particle moving on a line. The state space for such a particle is L2, the Hilbert space of complex-valued and square-integrable ...
in the momentum basis:
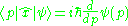
and other useful relations:

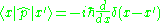
where
 stands for Dirac's delta function.
stands for Dirac's delta function.Derivation
Suppose we have an infinitesimal translation operatorTranslation operator
The translation operator can refer to these things:* A shift operator, which effects a geometric translation. See also Translation .* An alternative name for the displacement operator in quantum optics....
 , where
, where  represents the length of the infinitesimal translation, then
represents the length of the infinitesimal translation, then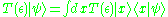
that becomes
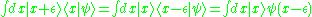
We assume the function
 to be analytic
to be analyticAnalytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
(or simply differentiable, for simplicity), so we may write:
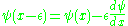
so we have for infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
values of epsilon:
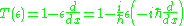
we know from classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
that momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
is the generator of translation
Translation (physics)
In physics, translation is movement that changes the position of an object, as opposed to rotation. For example, according to Whittaker:...
, so we know that
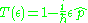
thus
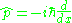
Canonical commutation relation
One can easily show that by appropriately using the momentum basis and the position basis: