Representation theory of the Galilean group
Encyclopedia
In nonrelativistic quantum mechanics
, an account can be given of the existence of mass
and spin
as follows:
The spacetime symmetry group
of nonrelativistic quantum mechanics is the Galilean group. In 3+1 dimensions, this is the subgroup of the affine group
on (t,x,y,z) whose linear part leaves invariant both the metric
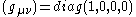and the (independent) dual metric
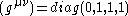. A similar definition applies for n+1 dimensions.
We are interested in projective representation
s of this group, which are equivalent to unitary representation
s of the nontrivial central extension of the universal covering group
of the Galilean group by the one dimensional Lie group R, refer to the article Galilean group for the central extension of its Lie algebra
. We will focus upon the Lie algebra here because it is simpler to analyze and we can always extend the results to the full Lie group thanks to the Frobenius theorem
.
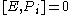
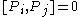
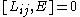
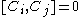
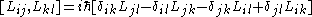
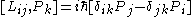
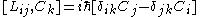
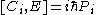
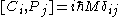
If you think about how spatial and time translations, rotations and boosts work, these relations are intuitive (except for the central extension).
The central charge
M is of course a Casimir invariant
. The mass shell invariant
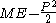
is a second Casimir invariant
. In 3+1 dimensions, a third Casimir invariant
is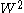
where
.
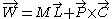More generally, in n+1 dimensions, invariants will be a function of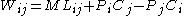
and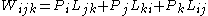 
, as well as of the mass shell invariant and central charge.
Using Schur's lemma
, in an irreducible unitary representation, each of these Casimir invariants are multiples of the identity. Let's call these coefficients m and mE0 and (in the case of 3+1 dimensions) w respectively. Remember we are talking about unitary representations here, which means these values have to be real
. So, m > 0, m = 0 and m < 0. The last case is similar to the first.
In 3+1 dimensions, when m>0, for the third invariant, we can write,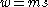
, where 
represents the spin, or intrinsic angular momentum. More generally, in n+1 dimensions, the generators L and C will be related, respectively, to the total angular momentum and center of mass moment by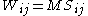
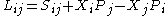
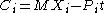
where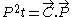
.
From a purely representation theoretic point of view, we'd have to study all of the representations, but we are interested in applications to quantum mechanics here. There, E represents the energy
, which has to be bounded from below if we require thermodynamic stability. Consider first the case where m is nonzero. If we look at the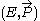
space with the constraint
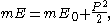
we find the boosts act transitively on this hypersurface. In fact, treating the energy E as the Hamiltonian, differentiating with respect to P, and applying Hamilton's equations, we obtain the mass-velocity relation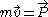
. The hypersurface is parametrized by the velocity 
.
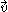Look at the stabilizer of a point on the orbit, (E0, 0), corresponding to where the velocity is 0. Because of transitivity, we know the unitary irrep contains a nontrivial subspace
with these energy-momentum eigenvalues. (This subspace only exists in a rigged Hilbert space
because the momentum spectrum is continuous.) It is spanned by E,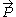
, M and Lij. We already know how the subspace of the irrep transforms under all but the angular momentum
. Note that the rotation subgroup is Spin(3). We have to look at its double cover because we're considering projective representations. This is called the little group, a name given by Eugene Wigner. The method of induced representations tells us the irrep is given by the direct sum of all the fibers in a vector bundle
over the mE = mE0 + P2/2 hypersurface whose fibers are a unitary irrep of Spin(3). Spin(3) is none other than SU(2). See representation theory of SU(2)
. There, it is shown the unitary irreps of SU(2) are labeled by s, a nonnegative integer multiple of one half. This is called the spin
, due to historical reasons. So, we have shown for m not equal to zero, the unitary irreps are classified by m, E0 and a spin s. Looking at the spectrum of E, we find that if m, the mass, is negative, the spectrum of E is not bounded from below. So, only the case with a positive mass is physical.
Now, let's look at the case where m = 0. Because of unitarity,
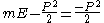
is nonpositive. Suppose it is zero. Here, the boosts and the rotations form the little group. So, any unitary irrep of this little group also gives rise to a projective irrep of the Galilean group. As far as we can tell, only the case which transforms trivially under the little group has any physical interpretation and it corresponds to the no particle state (vacuum
).
The case where the invariant is negative requires additional comment. This corresponds to the representation class for m = 0 and non-zero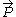
. Extending the bradyon
, luxon
, tachyon
classification from the representation theory of the Poincaré' group to an analogous classification, here, one may term these states as synchrons. They represent an instantaneous transfer of non-zero momentum across a (possibly large) distance. Associated with them is a 'time' operator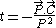
which may be identified the time of transfer. These states are naturally interpreted as the carriers of instantaneous action-at-a-distance forces.
In the 3+1-dimensional Galilei group, the boost generator may be decomposed into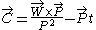
with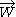
playing a role analogous to helicity
.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, an account can be given of the existence of mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
and spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
as follows:
The spacetime symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of nonrelativistic quantum mechanics is the Galilean group. In 3+1 dimensions, this is the subgroup of the affine group
Affine group
In mathematics, the affine group or general affine group of any affine space over a field K is the group of all invertible affine transformations from the space into itself.It is a Lie group if K is the real or complex field or quaternions....
on (t,x,y,z) whose linear part leaves invariant both the metric
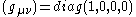and the (independent) dual metric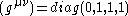. A similar definition applies for n+1 dimensions.We are interested in projective representation
Projective representation
In the mathematical field of representation theory, a projective representation of a group G on a vector space V over a field F is a group homomorphism from G to the projective linear groupwhere GL is the general linear group of invertible linear transformations of V over F and F* here is the...
s of this group, which are equivalent to unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
s of the nontrivial central extension of the universal covering group
Universal covering group
In mathematics, a covering group of a topological group H is a covering space G of H such that G is a topological group and the covering map p : G → H is a continuous group homomorphism. The map p is called the covering homomorphism...
of the Galilean group by the one dimensional Lie group R, refer to the article Galilean group for the central extension of its Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
. We will focus upon the Lie algebra here because it is simpler to analyze and we can always extend the results to the full Lie group thanks to the Frobenius theorem
Frobenius theorem (differential topology)
In mathematics, Frobenius' theorem gives necessary and sufficient conditions for finding a maximal set of independent solutions of an overdetermined system of first-order homogeneous linear partial differential equations...
.
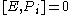
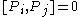
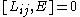
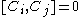
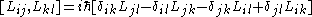
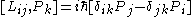
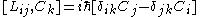
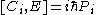
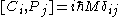
If you think about how spatial and time translations, rotations and boosts work, these relations are intuitive (except for the central extension).
The central charge
Central charge
In theoretical physics, a central charge is an operator Z that commutes with all the other symmetry operators. The adjective "central" refers to the center of the symmetry group -- the subgroup of elements that commute with all other elements of the original group—or to the center of a Lie algebra...
M is of course a Casimir invariant
Casimir invariant
In mathematics, a Casimir invariant or Casimir operator is a distinguished element of the centre of the universal enveloping algebra of a Lie algebra...
. The mass shell invariant
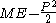
is a second Casimir invariant
Casimir invariant
In mathematics, a Casimir invariant or Casimir operator is a distinguished element of the centre of the universal enveloping algebra of a Lie algebra...
. In 3+1 dimensions, a third Casimir invariant
Casimir invariant
In mathematics, a Casimir invariant or Casimir operator is a distinguished element of the centre of the universal enveloping algebra of a Lie algebra...
is
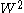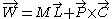where.More generally, in n+1 dimensions, invariants will be a function of
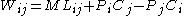and 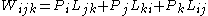, as well as of the mass shell invariant and central charge.Using Schur's lemma
Schur's lemma
In mathematics, Schur's lemma is an elementary but extremely useful statement in representation theory of groups and algebras. In the group case it says that if M and N are two finite-dimensional irreducible representations...
, in an irreducible unitary representation, each of these Casimir invariants are multiples of the identity. Let's call these coefficients m and mE0 and (in the case of 3+1 dimensions) w respectively. Remember we are talking about unitary representations here, which means these values have to be real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
. So, m > 0, m = 0 and m < 0. The last case is similar to the first.
In 3+1 dimensions, when m>0, for the third invariant, we can write,
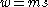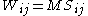
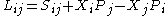
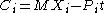
, where represents the spin, or intrinsic angular momentum. More generally, in n+1 dimensions, the generators L and C will be related, respectively, to the total angular momentum and center of mass moment bywhere
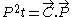.From a purely representation theoretic point of view, we'd have to study all of the representations, but we are interested in applications to quantum mechanics here. There, E represents the energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
, which has to be bounded from below if we require thermodynamic stability. Consider first the case where m is nonzero. If we look at the
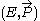space with the constraint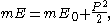we find the boosts act transitively on this hypersurface. In fact, treating the energy E as the Hamiltonian, differentiating with respect to P, and applying Hamilton's equations, we obtain the mass-velocity relation
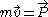. The hypersurface is parametrized by the velocity 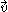.Look at the stabilizer of a point on the orbit, (E0, 0), corresponding to where the velocity is 0. Because of transitivity, we know the unitary irrep contains a nontrivial subspace
Subspace
-In mathematics:* Euclidean subspace, in linear algebra, a set of vectors in n-dimensional Euclidean space that is closed under addition and scalar multiplication...
with these energy-momentum eigenvalues. (This subspace only exists in a rigged Hilbert space
Rigged Hilbert space
In mathematics, a rigged Hilbert space is a construction designed to link the distribution and square-integrable aspects of functional analysis. Such spaces were introduced to study spectral theory in the broad sense...
because the momentum spectrum is continuous.) It is spanned by E,
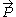, M and Lij. We already know how the subspace of the irrep transforms under all but the angular momentumAngular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
. Note that the rotation subgroup is Spin(3). We have to look at its double cover because we're considering projective representations. This is called the little group, a name given by Eugene Wigner. The method of induced representations tells us the irrep is given by the direct sum of all the fibers in a vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
over the mE = mE0 + P2/2 hypersurface whose fibers are a unitary irrep of Spin(3). Spin(3) is none other than SU(2). See representation theory of SU(2)
Representation theory of SU(2)
In the study of the representation theory of Lie groups, the study of representations of SU is fundamental to the study of representations of semisimple Lie groups. It is the first case of a Lie group that is both a compact group and a non-abelian group...
. There, it is shown the unitary irreps of SU(2) are labeled by s, a nonnegative integer multiple of one half. This is called the spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
, due to historical reasons. So, we have shown for m not equal to zero, the unitary irreps are classified by m, E0 and a spin s. Looking at the spectrum of E, we find that if m, the mass, is negative, the spectrum of E is not bounded from below. So, only the case with a positive mass is physical.
Now, let's look at the case where m = 0. Because of unitarity,
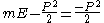
is nonpositive. Suppose it is zero. Here, the boosts and the rotations form the little group. So, any unitary irrep of this little group also gives rise to a projective irrep of the Galilean group. As far as we can tell, only the case which transforms trivially under the little group has any physical interpretation and it corresponds to the no particle state (vacuum
Vacuum state
In quantum field theory, the vacuum state is the quantum state with the lowest possible energy. Generally, it contains no physical particles...
).
The case where the invariant is negative requires additional comment. This corresponds to the representation class for m = 0 and non-zero
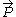. Extending the bradyonBradyon
A bradyon, also known as a tardyon or ittyon, is a particle that travels slower than light. All known particles that have mass are bradyons...
, luxon
Luxon
In particle physics, a massless particle is a particle whose invariant mass is zero. Currently, the only known massless particles are gauge bosons: the photon and the gluon...
, tachyon
Tachyon
A tachyon is a hypothetical subatomic particle that always moves faster than light. In the language of special relativity, a tachyon would be a particle with space-like four-momentum and imaginary proper time. A tachyon would be constrained to the space-like portion of the energy-momentum graph...
classification from the representation theory of the Poincaré' group to an analogous classification, here, one may term these states as synchrons. They represent an instantaneous transfer of non-zero momentum across a (possibly large) distance. Associated with them is a 'time' operator
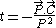
which may be identified the time of transfer. These states are naturally interpreted as the carriers of instantaneous action-at-a-distance forces.
In the 3+1-dimensional Galilei group, the boost generator may be decomposed into
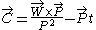
with
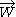playing a role analogous to helicityHelicity
The term helicity has several meanings. In physics, all referring to a phenomenon that resembles a helix. See:*helicity , the extent to which corkscrew-like motion occurs...
.
See also
- Representation theory of the Poincaré groupRepresentation theory of the Poincaré groupIn mathematics, the representation theory of the Poincaré group is an example of the representation theory of a Lie group that is neither a compact group nor a semisimple group. It is fundamental in theoretical physics....
- Wigner's classificationWigner's classificationIn mathematics and theoretical physics, Wigner's classificationis a classification of the nonnegative energy irreducible unitary representations of the Poincaré group, which have sharp mass eigenvalues...
- Representation theory of the diffeomorphism group
- Rotation operator