
Degeneracy (mathematics)
Encyclopedia
In mathematics
, a degenerate case is a limiting case in which a class of object changes its nature so as to belong to another, usually simpler, class.
A degenerate case thus has special features, which depart from the properties that are generic
in the wider class, and which would be lost under an appropriate small perturbation
.
Similarly, roots of a polynomial
are said to be degenerate if they coincide, since generically the n roots of an nth degree polynomial are all distinct. This usage carries over to eigenproblems: a degenerate eigenvalue (i.e. a multiply coinciding root of the characteristic polynomial
) is one that has more than one linearly independent eigenvector.
In quantum mechanics
any such multiplicity
in the eigenvalues of the Hamiltonian operator gives rise to degenerate energy level
s. Usually any such degeneracy indicates some underlying symmetry
in the system.
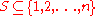 , there is a bounded, axis-aligned degenerate rectangle
, there is a bounded, axis-aligned degenerate rectangle
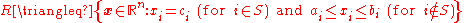
where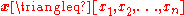 and
and 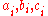 are constant (with
are constant (with 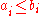 for all
for all 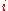 ). The number of degenerate sides of
). The number of degenerate sides of  is the number of elements of the subset
is the number of elements of the subset 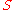 . Thus, there may be as few as one degenerate "side" or as many as
. Thus, there may be as few as one degenerate "side" or as many as  (in which case
(in which case  reduces to a singleton point).
reduces to a singleton point).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a degenerate case is a limiting case in which a class of object changes its nature so as to belong to another, usually simpler, class.
A degenerate case thus has special features, which depart from the properties that are generic
Generic property
In mathematics, properties that hold for "typical" examples are called generic properties. For instance, a generic property of a class of functions is one that is true of "almost all" of those functions, as in the statements, "A generic polynomial does not have a root at zero," or "A generic...
in the wider class, and which would be lost under an appropriate small perturbation
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
.
- A pointPoint (geometry)In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
is a degenerate circleCircleA circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
, namely one with radius 0. - A circle is a degenerate form of an ellipseEllipseIn geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
, namely one with eccentricityEccentricity (mathematics)In mathematics, the eccentricity, denoted e or \varepsilon, is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.In particular,...
0. - The lineLine (mathematics)The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
is a degenerate form of a parabolaParabolaIn mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
if the parabola resides on a tangent plane. - A segmentLine segmentIn geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
is a degenerate form of a rectangleRectangleIn Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
, if this has a side of length 0. - A hyperbolaHyperbolaIn mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
can degenerate into two lines crossing at a point, through a family of hyperbolas having those lines as common asymptoteAsymptoteIn analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors...
s. - A set containing a single point is a degenerate continuumLinear continuumIn the mathematical field of order theory, a continuum or linear continuum is a generalization of the real line.Formally, a linear continuum is a linearly ordered set S of more than one element that is densely ordered, i.e., between any two members there is another, and which "lacks gaps" in the...
. - A random variable which can only take one value has a degenerate distribution.
- A sphereSphereA sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
is a degenerate standard torus where the axis of revolution passes through the center of the generating circle, rather than outside it. - A degenerate triangleTriangleA triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
has collinear vertices. - See "general positionGeneral positionIn algebraic geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the general case situation, as opposed to some more special or coincidental cases that are possible...
" for other examples.
Similarly, roots of a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
are said to be degenerate if they coincide, since generically the n roots of an nth degree polynomial are all distinct. This usage carries over to eigenproblems: a degenerate eigenvalue (i.e. a multiply coinciding root of the characteristic polynomial
Characteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
) is one that has more than one linearly independent eigenvector.
In quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
any such multiplicity
Multiplicity (mathematics)
In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point....
in the eigenvalues of the Hamiltonian operator gives rise to degenerate energy level
Degenerate energy level
In physics, two or more different quantum states are said to be degenerate if they are all at the same energy level. Statistically this means that they are all equally probable of being filled, and in Quantum Mechanics it is represented mathematically by the Hamiltonian for the system having more...
s. Usually any such degeneracy indicates some underlying symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
in the system.
Degenerate rectangle
For any non-empty subset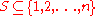 , there is a bounded, axis-aligned degenerate rectangle
, there is a bounded, axis-aligned degenerate rectangle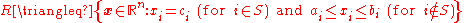
where
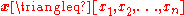 and
and 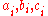 are constant (with
are constant (with 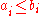 for all
for all 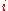 ). The number of degenerate sides of
). The number of degenerate sides of  is the number of elements of the subset
is the number of elements of the subset 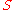 . Thus, there may be as few as one degenerate "side" or as many as
. Thus, there may be as few as one degenerate "side" or as many as  (in which case
(in which case  reduces to a singleton point).
reduces to a singleton point).See also
- Vacuous truthVacuous truthA vacuous truth is a truth that is devoid of content because it asserts something about all members of a class that is empty or because it says "If A then B" when in fact A is inherently false. For example, the statement "all cell phones in the room are turned off" may be true...
- Trivial (mathematics)Trivial (mathematics)In mathematics, the adjective trivial is frequently used for objects that have a very simple structure...
- Pathological (mathematics)Pathological (mathematics)In mathematics, a pathological phenomenon is one whose properties are considered atypically bad or counterintuitive; the opposite is well-behaved....
- Degenerate formDegenerate formIn mathematics, specifically linear algebra, a degenerate bilinear form ƒ on a vector space V is one such that the map from V to V^* given by v \mapsto is not an isomorphism...

