Krull dimension
Encyclopedia
In commutative algebra
, the Krull dimension of a ring
R, named after Wolfgang Krull
(1899–1971), is the supremum of the number of strict inclusions in a chain of prime ideals. The Krull dimension need not be finite even for a Noetherian ring
.
A field k has Krull dimension 0; more generally,
has Krull dimension n. A principal ideal domain
that is not a field has Krull dimension 1.
is of length n. That is, it is counting the number of strict inclusions, not the number of primes, although these only differ by 1. Given a prime
, we define the height of 
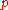, written 
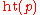to be the supremum of the set
We define the Krull dimension of
to be the supremum of the heights of all of its primes.
Nagata gave an example of a ring that has infinite Krull dimension even though every prime ideal has finite height. Nagata also gave an example of a Noetherian ring where not every chain can be extended to a maximal chain. Rings in which every chain of prime ideals can be extended to a maximal chain are known as catenary ring
s.
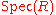, the space of prime ideals of 
equipped with the Zariski topology, that the Krull dimension of 
is precisely equal to the irreducible dimension of its spectrum. This follows immediately from the Galois connection
between ideals of
and closed subsets of 
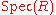and the elementary observation that the prime ideals of 
correspond by the definition of the spectrum to the generic points of the closed subsets they to which they correspond under the Galois connection.
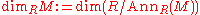
where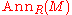
, the annihilator
, is the kernel of the natural map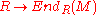
of R into the ring of 
-linear endomorphisms on 
.
In the language of schemes, finite type modules are interpreted as coherent sheaves, or generalized finite rank vector bundles.
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, the Krull dimension of a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R, named after Wolfgang Krull
Wolfgang Krull
Wolfgang Krull was a German mathematician working in the field of commutative algebra.He was born in Baden-Baden, Imperial Germany and died in Bonn, West Germany.- See also :* Krull dimension* Krull topology...
(1899–1971), is the supremum of the number of strict inclusions in a chain of prime ideals. The Krull dimension need not be finite even for a Noetherian ring
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
.
A field k has Krull dimension 0; more generally,
has Krull dimension n. A principal ideal domainPrincipal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
that is not a field has Krull dimension 1.
Explanation
We say that a strict chain of inclusions of prime ideals of the form:is of length n. That is, it is counting the number of strict inclusions, not the number of primes, although these only differ by 1. Given a prime
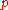, we define the height of , written 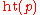to be the supremum of the setWe define the Krull dimension of
to be the supremum of the heights of all of its primes.Nagata gave an example of a ring that has infinite Krull dimension even though every prime ideal has finite height. Nagata also gave an example of a Noetherian ring where not every chain can be extended to a maximal chain. Rings in which every chain of prime ideals can be extended to a maximal chain are known as catenary ring
Catenary ring
In mathematics, a commutative ring R is catenary if for any pair of prime idealsany two strictly increasing chainsare contained in maximal strictly increasing chains from p to q of the same length. In other words, there is a well-defined function from pairs of prime ideals to natural numbers,...
s.
Krull dimension and schemes
It follows readily from the definition of the spectrum of a ringSpectrum of a ring
In abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
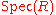, the space of prime ideals of equipped with the Zariski topology, that the Krull dimension of is precisely equal to the irreducible dimension of its spectrum. This follows immediately from the Galois connectionGalois connection
In mathematics, especially in order theory, a Galois connection is a particular correspondence between two partially ordered sets . The same notion can also be defined on preordered sets or classes; this article presents the common case of posets. Galois connections generalize the correspondence...
between ideals of
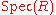and closed subsets of and the elementary observation that the prime ideals of correspond by the definition of the spectrum to the generic points of the closed subsets they to which they correspond under the Galois connection.Examples
- The dimension of a polynomial ringPolynomial ringIn mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
over a field
is the number of indeterminates. These rings correspond to affine spaces in the language of schemes, so this result can be thought of as foundational. In general, if R is a NoetherianNoetherian ringIn mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
ring, then the dimension of R[x] is d + 1. If the Noetherianity hypothesis is dropped, then R[x] can have dimension anywhere between d + 1 and 2d + 1.
- The ring of integers
has dimension 1.
- An integral domain is a field if and only if its Krull dimension is zero. Dedekind domainDedekind domainIn abstract algebra, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily unique up to the order of the factors...
s that are not fields (for example, discrete valuation ringDiscrete valuation ringIn abstract algebra, a discrete valuation ring is a principal ideal domain with exactly one non-zero maximal ideal.This means a DVR is an integral domain R which satisfies any one of the following equivalent conditions:...
s) have dimension one. In general, a NoetherianNoetherian ringIn mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
ring is ArtinianArtinian ringIn abstract algebra, an Artinian ring is a ring that satisfies the descending chain condition on ideals. They are also called Artin rings and are named after Emil Artin, who first discovered that the descending chain condition for ideals simultaneously generalizes finite rings and rings that are...
if and only if its Krull dimension is 0.
Krull Dimension of a Module
If R is a commutative ring, and M is an R-module, we define the Krull dimension of M to be the Krull dimension of the quotient of R making M a faithful module. That is, we define it by the formula: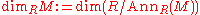where
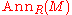, the annihilatorAnnihilator
Annihilator may refer to:* Annihilator , a mathematical concept* The annihilator of a vector subspace* Annihilator method, a type of differential operator, used in a particular method for solving differential equations...
, is the kernel of the natural map
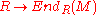of R into the ring of -linear endomorphisms on .In the language of schemes, finite type modules are interpreted as coherent sheaves, or generalized finite rank vector bundles.