E. T. Whittaker
Encyclopedia
Edmund Taylor Whittaker FRS FRSE (24 October 1873–24 March 1956) was an English
mathematician
who contributed widely to applied mathematics
, mathematical physics
and the theory of special functions
. He had a particular interest in numerical analysis
, but also worked on celestial mechanics
and the history of physics
. Near the end of his career he received the Copley Medal
, the most prestigious honorary award in British science. The School of Mathematics of the University of Edinburgh holds The Whittaker Colloquium, a yearly lecture in his honoour.
, in Lancashire
. He was educated at Manchester Grammar School
and Trinity College, Cambridge
from 1892. He graduated as Second Wrangler in the examination in 1895 and also received the Tyson Medal for Mathematics and Astronomy. In 1896, Whittaker was elected as a fellow of Trinity College, Cambridge, and remained at Cambridge as a teacher until 1906. Between 1906 and 1911 he was the Royal Astronomer of Ireland and professor of astronomy at Trinity College Dublin where he taught mathematical physics. In 1911 Whittaker became professor at Edinburgh University and remained there for the rest of his career.
Whittaker was a Christian
and became a convert to the Roman Catholic Church
(1930). In relation to that he was a member of the Pontifical Academy of Sciences
from 1936 onward and was president of a Newman Society. Earlier at Cambridge in 1901 he married the daughter of a learned Presbyterian minister. They had five children, including the mathematician John Macnaughten Whittaker, (1905-1984) and his elder daughter, Beatrice, married the man later to become Professor of Maths at St. Andrew's University, ET Copson.
Whittaker wrote the biography of a famous Italian mathematician, Vito Volterra
for Royal Society in 1941.
Whittaker was, in 1954, selected by the Fellows of the Royal Society to receive the Copley Medal
, the highest award granted by the scientific Royal Society of London, "for his distinguished contributions to both pure and applied mathematics and to theoretical physics". Back in 1931 Whittaker had received the Royal Society's Sylvester Medal
"for his original contributions to both pure and applied mathematics". Whittaker died in Edinburgh, Scotland.
, one of the handful of mathematics texts of its era to become indispensable. This work has remained in print continuously for over a century.
of the Whittaker function
or Whittaker integral, in the theory of confluent hypergeometric function
s. This makes him also the eponym of the Whittaker model
in the local theory of automorphic representations. He published also on algebraic function
s and automorphic function
s. He gave expression
s for the Bessel function
s as integral
s involving Legendre function
s.
s, Whittaker developed a general solution of the Laplace equation in three dimension
s and the solution of the wave equation
. He developed the electrical potential field
as a bi-directional flow of energy
(sometimes referred to as alternating current
s). Whittaker's pair of papers in 1903 and 1904 indicated that any potential
can be analysed by a Fourier
-like series of waves, such as a planet
's gravitational field
point-charge
. The superpositions of inward and outward wave pairs produce the "static" fields (or scalar potential
). These were harmonic
ally-related. By this conception, the structure of electric potential
is created from two opposite, though balanced, parts. Whittaker suggested that gravity possessed a wavelike "undulatory
" character.
and Electricity
", which gave a very detailed account of the aether theories
from René Descartes
to Hendrik Lorentz
, and which made Whittaker a respected historian of science. Though the book was a "History", apparently Whittaker innovated the use of the rapidity
parameter in his exposition of relativity.
Furthermore, he provided a rather succinct summary of relativity theory:
In 1951 (Vol. 1) and 1953 (Vol. 2), he published an extended and revised edition of his book in two volumes. The second volume contains some interesting historical remarks. For example, it contains a chapter named "The Relativity Theory of Poincaré and Lorentz", where Whittaker credited Henri Poincaré
and Lorentz for developing special relativity
, and he attributed to Albert Einstein
's relativity paper only little importance. He also attributed the formula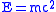
to Poincaré. In 1984 Clifford Truesdell
wrote that Whittaker "aroused colossal antagonism by trying to set the record straight on the basis of print and record rather than recollection and folklore and professional propaganda,..."
's Fundamental Theory (1946), and wrote
From Euclid to Eddington, A Study of Conceptions of the External World (1949), including a first scholarly account of some of the research between 1900 to 1925.
English people
The English are a nation and ethnic group native to England, who speak English. The English identity is of early mediaeval origin, when they were known in Old English as the Anglecynn. England is now a country of the United Kingdom, and the majority of English people in England are British Citizens...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
who contributed widely to applied mathematics
Applied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
, mathematical physics
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
and the theory of special functions
Special functions
Special functions are particular mathematical functions which have more or less established names and notations due to their importance in mathematical analysis, functional analysis, physics, or other applications....
. He had a particular interest in numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, but also worked on celestial mechanics
Celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of celestial objects. The field applies principles of physics, historically classical mechanics, to astronomical objects such as stars and planets to produce ephemeris data. Orbital mechanics is a subfield which focuses on...
and the history of physics
History of physics
As forms of science historically developed out of philosophy, physics was originally referred to as natural philosophy, a term describing a field of study concerned with "the workings of nature".-Early history:...
. Near the end of his career he received the Copley Medal
Copley Medal
The Copley Medal is an award given by the Royal Society of London for "outstanding achievements in research in any branch of science, and alternates between the physical sciences and the biological sciences"...
, the most prestigious honorary award in British science. The School of Mathematics of the University of Edinburgh holds The Whittaker Colloquium, a yearly lecture in his honoour.
Biography
Whittaker was born in SouthportSouthport
Southport is a seaside town in the Metropolitan Borough of Sefton in Merseyside, England. During the 2001 census Southport was recorded as having a population of 90,336, making it the eleventh most populous settlement in North West England...
, in Lancashire
Lancashire
Lancashire is a non-metropolitan county of historic origin in the North West of England. It takes its name from the city of Lancaster, and is sometimes known as the County of Lancaster. Although Lancaster is still considered to be the county town, Lancashire County Council is based in Preston...
. He was educated at Manchester Grammar School
Manchester Grammar School
The Manchester Grammar School is the largest independent day school for boys in the UK . It is based in Manchester, England...
and Trinity College, Cambridge
Trinity College, Cambridge
Trinity College is a constituent college of the University of Cambridge. Trinity has more members than any other college in Cambridge or Oxford, with around 700 undergraduates, 430 graduates, and over 170 Fellows...
from 1892. He graduated as Second Wrangler in the examination in 1895 and also received the Tyson Medal for Mathematics and Astronomy. In 1896, Whittaker was elected as a fellow of Trinity College, Cambridge, and remained at Cambridge as a teacher until 1906. Between 1906 and 1911 he was the Royal Astronomer of Ireland and professor of astronomy at Trinity College Dublin where he taught mathematical physics. In 1911 Whittaker became professor at Edinburgh University and remained there for the rest of his career.
Whittaker was a Christian
Christian
A Christian is a person who adheres to Christianity, an Abrahamic, monotheistic religion based on the life and teachings of Jesus of Nazareth as recorded in the Canonical gospels and the letters of the New Testament...
and became a convert to the Roman Catholic Church
Roman Catholic Church
The Catholic Church, also known as the Roman Catholic Church, is the world's largest Christian church, with over a billion members. Led by the Pope, it defines its mission as spreading the gospel of Jesus Christ, administering the sacraments and exercising charity...
(1930). In relation to that he was a member of the Pontifical Academy of Sciences
Pontifical Academy of Sciences
The Pontifical Academy of Sciences is a scientific academy of the Vatican, founded in 1936 by Pope Pius XI. It is placed under the protection of the reigning Supreme Pontiff. Its aim is to promote the progress of the mathematical, physical and natural sciences and the study of related...
from 1936 onward and was president of a Newman Society. Earlier at Cambridge in 1901 he married the daughter of a learned Presbyterian minister. They had five children, including the mathematician John Macnaughten Whittaker, (1905-1984) and his elder daughter, Beatrice, married the man later to become Professor of Maths at St. Andrew's University, ET Copson.
Whittaker wrote the biography of a famous Italian mathematician, Vito Volterra
Vito Volterra
Vito Volterra was an Italian mathematician and physicist, known for his contributions to mathematical biology and integral equations....
for Royal Society in 1941.
Whittaker was, in 1954, selected by the Fellows of the Royal Society to receive the Copley Medal
Copley Medal
The Copley Medal is an award given by the Royal Society of London for "outstanding achievements in research in any branch of science, and alternates between the physical sciences and the biological sciences"...
, the highest award granted by the scientific Royal Society of London, "for his distinguished contributions to both pure and applied mathematics and to theoretical physics". Back in 1931 Whittaker had received the Royal Society's Sylvester Medal
Sylvester Medal
The Sylvester Medal is a bronze medal awarded by the Royal Society for the encouragement of mathematical research, and accompanied by a £1,000 prize...
"for his original contributions to both pure and applied mathematics". Whittaker died in Edinburgh, Scotland.
Whittaker & Watson
Whittaker is remembered as the author of A Course of Modern Analysis (1902), which in its 1915 second edition in collaboration with George Neville Watson became Whittaker and WatsonWhittaker and Watson
Whittaker and Watson is the informal name of a book formally titled A Course of Modern Analysis, written by E. T. Whittaker and G. N. Watson, first published by Cambridge University Press in 1902...
, one of the handful of mathematics texts of its era to become indispensable. This work has remained in print continuously for over a century.
Special functions
Whittaker is the eponymEponym
An eponym is the name of a person or thing, whether real or fictitious, after which a particular place, tribe, era, discovery, or other item is named or thought to be named...
of the Whittaker function
Whittaker function
In mathematics, a Whittaker function is a special solution of Whittaker's equation, a modified form of the confluent hypergeometric equation introduced by to make the formulas involving the solutions more symmetric...
or Whittaker integral, in the theory of confluent hypergeometric function
Confluent hypergeometric function
In mathematics, a confluent hypergeometric function is a solution of a confluent hypergeometric equation, which is a degenerate form of a hypergeometric differential equation where two of the three regular singularities merge into an irregular singularity...
s. This makes him also the eponym of the Whittaker model
Whittaker model
In representation theory, a branch of mathematics, the Whittaker model is a realization of a representation of a reductive algebraic group such as GL2 over a finite or local or global field on a space of functions on the group. It is named after E. T...
in the local theory of automorphic representations. He published also on algebraic function
Algebraic function
In mathematics, an algebraic function is informally a function that satisfies a polynomial equation whose coefficients are themselves polynomials with rational coefficients. For example, an algebraic function in one variable x is a solution y for an equationwhere the coefficients ai are polynomial...
s and automorphic function
Automorphic function
In mathematics, an automorphic function is a function on a space that is invariant under the action of some group, in other words a function on the quotient space. Often the space is a complex manifold and the group is a discrete group....
s. He gave expression
Expression (mathematics)
In mathematics, an expression is a finite combination of symbols that is well-formed according to rules that depend on the context. Symbols can designate numbers , variables, operations, functions, and other mathematical symbols, as well as punctuation, symbols of grouping, and other syntactic...
s for the Bessel function
Bessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
s as integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
s involving Legendre function
Legendre function
In mathematics, the Legendre functions Pλ, Qλ and associated Legendre functions P, Q are generalizations of Legendre polynomials to non-integer degree.-Differential equation:...
s.
Partial differential equations
In the theory of partial differential equationPartial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s, Whittaker developed a general solution of the Laplace equation in three dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s and the solution of the wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
. He developed the electrical potential field
Potential
*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
as a bi-directional flow of energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
(sometimes referred to as alternating current
Alternating current
In alternating current the movement of electric charge periodically reverses direction. In direct current , the flow of electric charge is only in one direction....
s). Whittaker's pair of papers in 1903 and 1904 indicated that any potential
Potential
*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
can be analysed by a Fourier
Fourier
Fourier most commonly refers to Joseph Fourier , French mathematician and physicist, or the mathematics, physics, and engineering terms named in his honor for his work on the concepts underlying them:In mathematics:...
-like series of waves, such as a planet
Planet
A planet is a celestial body orbiting a star or stellar remnant that is massive enough to be rounded by its own gravity, is not massive enough to cause thermonuclear fusion, and has cleared its neighbouring region of planetesimals.The term planet is ancient, with ties to history, science,...
's gravitational field
Gravitational field
The gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses...
point-charge
Telluric current
A telluric current , or Earth current, is an electric current which moves underground or through the sea. Telluric currents result from both natural causes and human activity, and the discrete currents interact in a complex pattern...
. The superpositions of inward and outward wave pairs produce the "static" fields (or scalar potential
Scalar potential
A scalar potential is a fundamental concept in vector analysis and physics . The scalar potential is an example of a scalar field...
). These were harmonic
Harmonic
A harmonic of a wave is a component frequency of the signal that is an integer multiple of the fundamental frequency, i.e. if the fundamental frequency is f, the harmonics have frequencies 2f, 3f, 4f, . . . etc. The harmonics have the property that they are all periodic at the fundamental...
ally-related. By this conception, the structure of electric potential
Electric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
is created from two opposite, though balanced, parts. Whittaker suggested that gravity possessed a wavelike "undulatory
Oscillation
Oscillation is the repetitive variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples include a swinging pendulum and AC power. The term vibration is sometimes used more narrowly to mean a mechanical oscillation but sometimes...
" character.
History of science
In 1910, Whittaker wrote "A History of the Theories of AetherLuminiferous aether
In the late 19th century, luminiferous aether or ether, meaning light-bearing aether, was the term used to describe a medium for the propagation of light....
and Electricity
Electricity
Electricity is a general term encompassing a variety of phenomena resulting from the presence and flow of electric charge. These include many easily recognizable phenomena, such as lightning, static electricity, and the flow of electrical current in an electrical wire...
", which gave a very detailed account of the aether theories
Aether theories
Aether theories in early modern physics proposed the existence of a medium, the aether , a space-filling substance or field, thought to be necessary as a transmission medium for the propagation of electromagnetic waves...
from René Descartes
René Descartes
René Descartes ; was a French philosopher and writer who spent most of his adult life in the Dutch Republic. He has been dubbed the 'Father of Modern Philosophy', and much subsequent Western philosophy is a response to his writings, which are studied closely to this day...
to Hendrik Lorentz
Hendrik Lorentz
Hendrik Antoon Lorentz was a Dutch physicist who shared the 1902 Nobel Prize in Physics with Pieter Zeeman for the discovery and theoretical explanation of the Zeeman effect...
, and which made Whittaker a respected historian of science. Though the book was a "History", apparently Whittaker innovated the use of the rapidity
Rapidity
In relativity, rapidity is an alternative to speed as a framework for measuring motion. On parallel velocities rapidities are simply additive, unlike speeds at relativistic velocities. For low speeds, rapidity and speed are proportional, but for high speeds, rapidity takes a larger value. The...
parameter in his exposition of relativity.
Furthermore, he provided a rather succinct summary of relativity theory:
- ...the equation of the rectangular hyperbolaUnit hyperbolaIn geometry, the unit hyperbola is the set of points in the Cartesian plane that satisfies x^2 - y^2 = 1 . In the study of indefinite orthogonal groups, the unit hyperbola forms the basis for an alternative radial lengthWhereas the unit circle surrounds its center, the unit hyperbola requires the...
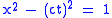in the plane of the variables (x, ct) is unaltered when any pair of conjugate diametersConjugate diametersIn geometry, two diameters of a conic section are said to be conjugate if each chord parallel to one diameter is bisected by the other diameter...
are taken as the new axis, and a new unit of length is taken proportional to the length of either of these diameters.
In 1951 (Vol. 1) and 1953 (Vol. 2), he published an extended and revised edition of his book in two volumes. The second volume contains some interesting historical remarks. For example, it contains a chapter named "The Relativity Theory of Poincaré and Lorentz", where Whittaker credited Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
and Lorentz for developing special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
, and he attributed to Albert Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
's relativity paper only little importance. He also attributed the formula
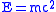to Poincaré. In 1984 Clifford TruesdellClifford Truesdell
Clifford Ambrose Truesdell III was an American mathematician, natural philosopher, historian of science, and polemicist.-Life:...
wrote that Whittaker "aroused colossal antagonism by trying to set the record straight on the basis of print and record rather than recollection and folklore and professional propaganda,..."
Applied mathematics and mathematical physics
Whittaker wrote The Calculus of Observations: a treatise on numerical mathematics (1924) and Treatise on the Analytical Dynamics of Particles and Rigid Bodies: With an Introduction to the Problem of Three Bodies (1937). He was the editor of EddingtonArthur Stanley Eddington
Sir Arthur Stanley Eddington, OM, FRS was a British astrophysicist of the early 20th century. He was also a philosopher of science and a popularizer of science...
's Fundamental Theory (1946), and wrote
From Euclid to Eddington, A Study of Conceptions of the External World (1949), including a first scholarly account of some of the research between 1900 to 1925.
Further reading
- A Course of Modern Analysis. 1902.
- "On the partial differential equations of mathematical physics". Math. Ann., Vol. 57, 1903, p.333–355.
- "On an expression of the electromagnetic field due to electrons by means of two scalar potential functions". Proc. Lond. Math. Soc. Series 2, Vol. 1, 1904, pp. 367–372.
- A Treatise on the Analytical Dynamics of Particles and Rigid Bodies. First Edition, Cambridge 1904.
- The Theory of Optical Instruments (Cambridge Tracts in Mathematics and Mathematical Physics No. 7), Cambridge 1907.
- Recent Researches on Space, Time, and Force, MNRAS, Vol. 70, pp. 363–366.
- A History of the theories of aether and electricity (1. edition), Dublin: Longman, Green and Co.
- "On the functions which are represented by the expansions of the interpolation theory," Proc. Royal Soc. Edinburgh, Sec. A, vol.35, pp.181–194, 1915.
- A Treatise on the Analytical Dynamics of Particles and Rigid Bodies. Second Edition, Cambridge 1917.
- "On the quantum mechanism in the atom". Proc. R. Soc. Edinb., Vol. 42, 1922, pp. 129–146
- A Short Course in Interpolation. London 1923.
- The Calculus of Observations: a treatise on numerical mathematics. 1924.
- Space and Spirit. Theories of the Universe and the Arguments for the Existence of God. 1946.
- The beginning and End of the World. Oxford 1942.
- Eddington’s Principle in the philosophy of Science. Cambridge 1951.
- A History of the theories of aether and electricity (2. edition), vol. 1: The classical theories / vol. 2: The modern theories 1900–1926, London: Nelson, ISBN 0-486-26126-3
- From Euclid to Eddington: A Study of Conceptions of the External World. Dover 1958.
- "Whittaker Memorial Volume". Proceedings of the Edinburgh Mathematical Society, 1958.
- Bearden, T. E., "Gravitobiology : Conception of Edmund Whittaker (papers of 1903-1904)". Tesla Book Co., Chula Vista, CA, USA.
External links
- Whittaker and the Aether at MathPages