Divisor function - AbsoluteAstronomy.com

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, and specifically in number theory

Number theory

Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...

, a divisor function is an arithmetical function related to the divisor

Divisor

In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...

s of an integer

Integer

The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships on the Riemann zeta function and the Eisenstein series

Eisenstein series

Eisenstein series, named after German mathematician Gotthold Eisenstein, are particular modular forms with infinite series expansions that may be written down directly...

of modular form

Modular form

In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...

s. Divisor functions were studied by Ramanujan, who gave a number of important congruences

Modular arithmetic

In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....

and identities

Identity (mathematics)

In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...

.

A related function is the divisor summatory function, which, as the name implies, is a sum over the divisor function.

Definition

The sum of positive divisors function σ_x(n), for a real or complex number x, is defined as the sum

SUM

SUM can refer to:* The State University of Management* Soccer United Marketing* Society for the Establishment of Useful Manufactures* StartUp-Manager* Software User’s Manual,as from DOD-STD-2 167A, and MIL-STD-498...

of the xth powers

Exponentiation

Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...

of the positive divisor

Divisor

In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...

s of n, or

The notations d(n), ν(n) and τ(n) (for the German Teiler = divisors) are also used to denote σ₀(n), or the number-of-divisors function . When x is 1, the function is called the sigma function or sum-of-divisors function, and the subscript is often omitted, so σ(n) is equivalent to σ₁(n) .
The aliquot sum s(n) of n is the sum of the proper divisors (that is, the divisors excluding n itself), and equals σ₁(n) − n; the aliquot sequence

Aliquot sequence

In mathematics, an aliquot sequence is a recursive sequence in which each term is the sum of the proper divisors of the previous term. The aliquot sequence starting with a positive integer k can be defined formally in terms of the sum-of-divisors function σ1 in the following way:For example, the...

of n is formed by repeatedly applying the aliquot sum function.

Example

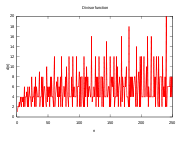
For example, σ₀(12) is the number of the divisors of 12:

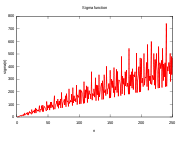
while σ₁(12) is the sum of all the divisors:

and the aliquot sum s(12) of proper divisors is:

Table of values

n	Divisors	σ₀(n)	σ₁(n)	s(n) = σ₁(n) − n	Comment
1	1	1	1	0	square number: σ₀(n) is odd; power of 2: s(n) = n − 1 (almost-perfect)
2	1,2	2	3	1
3	1,3	2	4	1
4	1,2,4	3	7	3	square number: σ₀(n) is odd; power of 2: s(n) = n − 1 (almost-perfect)
5	1,5	2	6	1
6	1,2,3,6	4	12	6	first perfect number Perfect number In number theory, a perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself . Equivalently, a perfect number is a number that is half the sum of all of its positive divisors i.e... : s(n) = n
7	1,7	2	8	1
8	1,2,4,8	4	15	7	power of 2: s(n) = n − 1 (almost-perfect)
9	1,3,9	3	13	4	square number: σ₀(n) is odd
10	1,2,5,10	4	18	8
11	1,11	2	12	1
12	1,2,3,4,6,12	6	28	16	first abundant number: s(n) > n
13	1,13	2	14	1
14	1,2,7,14	4	24	10
15	1,3,5,15	4	24	9
16	1,2,4,8,16	5	31	15	square number: σ₀(n) is odd; power of 2: s(n) = n − 1 (almost-perfect)

The cases , and so on are tabulated
in , , ,
, , ...

Properties

For a non-square integer every divisor d of n is paired with divisor n/d of n and

is then even; for a square integer one divisor (namely

) is not paired with a distinct divisor and

is then odd.

For a prime number

Prime number

A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...

because by definition, the factors of a prime number are 1 and itself. Also,where p_n# denotes the primorial

Primorial

In mathematics, and more particularly in number theory, primorial is a function from natural numbers to natural numbers similar to the factorial function, but rather than multiplying successive positive integers, only successive prime numbers are multiplied...

since n prime factors allow a sequence of binary selection (

or 1) from n terms for each proper divisor formed.

Clearly, 1 < d(n) < n and σ(n) > n for all n > 2.

The divisor function is multiplicative

Multiplicative function

In number theory, a multiplicative function is an arithmetic function f of the positive integer n with the property that f = 1 and whenevera and b are coprime, then...

, but not completely multiplicative

Completely multiplicative function

In number theory, functions of positive integers which respect products are important and are called completely multiplicative functions or totally multiplicative functions. Especially in number theory, a weaker condition is also important, respecting only products of coprime numbers, and such...

. The consequence of this is that, if we write

where r = ω(n) is the number of distinct prime factor

Prime factor

In number theory, the prime factors of a positive integer are the prime numbers that divide that integer exactly, without leaving a remainder. The process of finding these numbers is called integer factorization, or prime factorization. A prime factor can be visualized by understanding Euclid's...

s of n, p_i is the ith prime factor, and a_i is the maximum power of p_i by which n is divisible, then we have

which is equivalent to the useful formula:

It follows (by setting x = 0) that d(n) is:

For example, if n is 24, there are two prime factors (p₁ is 2; p₂ is 3); noting that 24 is the product of 2³×3¹, a₁ is 3 and a₂ is 1. Thus we can calculate d(24) as so:

The eight divisors counted by this formula are 1, 2, 4, 8, 3, 6, 12, and 24.

We also note s(n) = σ(n) − n. Here s(n) denotes the sum of the proper divisors of n, i.e. the divisors of n excluding n itself.
This function is the one used to recognize perfect number

Perfect number

In number theory, a perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself . Equivalently, a perfect number is a number that is half the sum of all of its positive divisors i.e...

s which are the n for which s(n) = n. If s(n) > n then n is an abundant number and if s(n) < n then n is a deficient number

Deficient number

In number theory, a deficient number or defective number is a number n for which the sum of divisors σIn number theory, a deficient number or defective number is a number n for which the sum of divisors σIn number theory, a deficient number or defective number is a number n for which...

.

If n is a power of 2, e.g.

, then

and s(n) = n - 1, which makes n almost-perfect

Almost perfect number

In mathematics, an almost perfect number is a natural number n such that the sum of all divisors of n is equal to 2n - 1, the sum of all proper divisors of n, s = σ - n, then being equal to n - 1...

.

As an example, for two distinct primes p and q with p < q, let

Then

and

where φ(n) is Euler's totient function.

Then, the roots of:

allows us to express p and q in terms of σ(n) and φ(n) only, without even knowing n or p+q, as:

Also, knowing n and either σ(n) or φ(n) (or knowing p+q and either σ(n) or φ(n)) allows us to easily find p and q.

In 1984, Roger Heath-Brown

Roger Heath-Brown

David Rodney "Roger" Heath-Brown F.R.S. , is a British mathematician working in the field of analytic number theory. He was an undergraduate and graduate student of Trinity College, Cambridge; his research supervisor was Alan Baker...

proved that

d(n) = d(n + 1)

will occur infinitely often.

Series relations

Two Dirichlet series involving the divisor function are:

which for d(n) = σ₀(n) gives

and

A Lambert series involving the divisor function is:

for arbitrary complex

Complex number

A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

|q| ≤ 1 and a. This summation also appears as the Fourier series of the Eisenstein series

Eisenstein series

Eisenstein series, named after German mathematician Gotthold Eisenstein, are particular modular forms with infinite series expansions that may be written down directly...

and the invariants of the Weierstrass elliptic functions.

Approximate growth rate

In little-o notation, the divisor function satisfies the inequality (see page 296 of Apostol’s book)

More precisely, Severin Wigert showed that

On the other hand, since there are infinitely many prime numbers,

In Big-O notation, Dirichlet showed that the average order

Average order of an arithmetic function

In number theory, the average order of an arithmetic function is some simpler or better-understood function which takes the same values "on average".Let f be an arithmetic function...

of the divisor function satisfies the following inequality (see Theorem 3.3 of Apostol’s book)

where

is Euler's constant

Euler–Mascheroni constant

The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....

. Improving the bound

in this formula is known as Dirichlet's divisor problem
The behaviour of the sigma function is irregular. The asymptotic growth rate of the sigma function can be expressed by:

where lim sup is the limit superior. This result is Grönwall
Thomas Hakon Grönwall
Thomas Hakon Grönwall or Thomas Hakon Gronwall was a Swedish mathematician. He studied at the University College of Stockholm and Uppsala University and completed his Ph.D. at Uppsala in 1898. Grönwall worked for about a year as a civil engineer in Germany before he immigrated to the United...

's theorem, published in 1913 . His proof uses Mertens' 3rd theorem

Mertens' theorems

In number theory, Mertens' theorems are three 1874 results related to the density of prime numbers proved by Franz Mertens...

, which says that

where p denotes a prime.

In 1915, Ramanujan proved that under the assumption of the Riemann hypothesis

Riemann hypothesis

In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...

, the inequality:

(Robin's inequality)
holds for all sufficiently large n. In 1984 Guy Robin proved that the inequality is true for all n ≥ 5,041 if and only if the Riemann hypothesis is true . This is Robin's theorem and the inequality became known after him. The largest known value that violates the inequality is n=5,040. If the Riemann hypothesis is true, there are no greater exceptions. If the hypothesis is false, then Robin showed there are an infinite number of values of n that violate the inequality, and it is known that the smallest such n ≥ 5,041 must be superabundant . It has been shown that the inequality holds for large odd and square-free integers, and that the Riemann hypothesis is equivalent to the inequality just for n divisible by the fifth power of a prime .

A related bound was given by Jeffrey Lagarias

Jeffrey Lagarias

Jeffrey Clark Lagarias is a mathematics professor at the University of Michigan.- Education :While in high school in 1966, Lagarias studied astronomy at the Summer Science Program....

in 2002, who proved that the Riemann hypothesis is equivalent to the statement that

for every natural number

Natural number

In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...

n, where

is the nth harmonic number, .

Robin also proved, unconditionally, that the inequality