Lambert series
Encyclopedia
In mathematics
, a Lambert series, named for Johann Heinrich Lambert
, is a series
taking the form
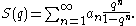
It can be resummed formally by expanding the denominator:
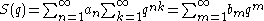
where the coefficients of the new series are given by the Dirichlet convolution
of an with the constant function 1(n) = 1:
This series may be inverted by means of the Möbius inversion formula
, and is an example of a Möbius transform.
will be exactly summable when used in a Lambert series. Thus, for example, one has
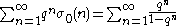
where
is the number of positive divisors
of the number n.
For the higher order sigma functions
, one has
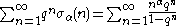
where
is any complex number
and
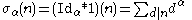
is the divisor function.
Lambert series in which the an are trigonometric function
s, for example, an = sin(2n x), can be evaluated by various combinations of the logarithmic derivative
s of Jacobi theta functions.
Other Lambert series include those for the Möbius function
:
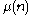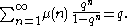
For Euler's totient function
:
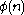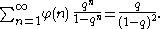
For Liouville's function
:
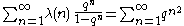
with the sum on the left similar to the Ramanujan theta function
.
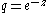one obtains another common form for the series, as
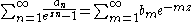
where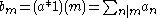
as before. Examples of Lambert series in this form, with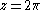
, occur in expressions for the Riemann zeta function for odd integer values; see Zeta constants for details.
is a polylogarithm function, we may refer to any sum of the form
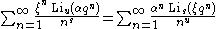
as a Lambert series, assuming that the parameters are suitably restricted. Thus
which holds for all complex q not on the unit circle, would be considered a Lambert series identity. This identity follows in a straightforward fashion from some identities published by the Indian mathematician S. Ramanujan. A very thorough exploration of Ramanujan's works can be found in the works by Bruce Berndt.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Lambert series, named for Johann Heinrich Lambert
Johann Heinrich Lambert
Johann Heinrich Lambert was a Swiss mathematician, physicist, philosopher and astronomer.Asteroid 187 Lamberta was named in his honour.-Biography:...
, is a series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
taking the form
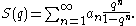
It can be resummed formally by expanding the denominator:
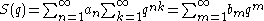
where the coefficients of the new series are given by the Dirichlet convolution
Dirichlet convolution
In mathematics, the Dirichlet convolution is a binary operation defined for arithmetic functions; it is important in number theory. It was developed by Johann Peter Gustav Lejeune Dirichlet, a German mathematician.-Definition:...
of an with the constant function 1(n) = 1:
This series may be inverted by means of the Möbius inversion formula
Möbius inversion formula
In mathematics, the classic Möbius inversion formula was introduced into number theory during the 19th century by August Ferdinand Möbius. Other Möbius inversion formulas are obtained when different local finite partially ordered sets replace the classic case of the natural numbers ordered by...
, and is an example of a Möbius transform.
Examples
Since this last sum is a typical number-theoretic sum, almost any natural multiplicative functionMultiplicative function
In number theory, a multiplicative function is an arithmetic function f of the positive integer n with the property that f = 1 and whenevera and b are coprime, then...
will be exactly summable when used in a Lambert series. Thus, for example, one has
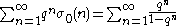
where
is the number of positive divisorsDivisor function
In mathematics, and specifically in number theory, a divisor function is an arithmetical function related to the divisors of an integer. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships...
of the number n.
For the higher order sigma functions
Divisor function
In mathematics, and specifically in number theory, a divisor function is an arithmetical function related to the divisors of an integer. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships...
, one has
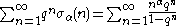
where
is any complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
and
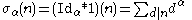
is the divisor function.
Lambert series in which the an are trigonometric function
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s, for example, an = sin(2n x), can be evaluated by various combinations of the logarithmic derivative
Logarithmic derivative
In mathematics, specifically in calculus and complex analysis, the logarithmic derivative of a function f is defined by the formulawhere f ′ is the derivative of f....
s of Jacobi theta functions.
Other Lambert series include those for the Möbius function
Möbius function
The classical Möbius function μ is an important multiplicative function in number theory and combinatorics. The German mathematician August Ferdinand Möbius introduced it in 1832...
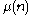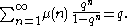
:For Euler's totient function
Euler's totient function
In number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
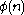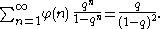
:For Liouville's function
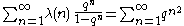
:with the sum on the left similar to the Ramanujan theta function
Ramanujan theta function
In mathematics, particularly q-analog theory, the Ramanujan theta function generalizes the form of the Jacobi theta functions, while capturing their general properties. In particular, the Jacobi triple product takes on a particularly elegant form when written in terms of the Ramanujan theta...
.
Alternate form
Substituting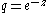 one obtains another common form for the series, as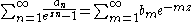where
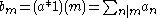
as before. Examples of Lambert series in this form, with
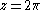, occur in expressions for the Riemann zeta function for odd integer values; see Zeta constants for details.Current usage
In the literature we find Lambert series applied to a wide variety of sums. For example, since is a polylogarithm function, we may refer to any sum of the form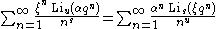as a Lambert series, assuming that the parameters are suitably restricted. Thus
which holds for all complex q not on the unit circle, would be considered a Lambert series identity. This identity follows in a straightforward fashion from some identities published by the Indian mathematician S. Ramanujan. A very thorough exploration of Ramanujan's works can be found in the works by Bruce Berndt.