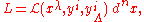Lagrangian system
Encyclopedia
In mathematics, a Lagrangian system is a pair  of a smooth
of a smooth
fiber bundle
 and a Lagrangian density
and a Lagrangian density  which yields the Euler-Lagrange differential operator
which yields the Euler-Lagrange differential operator
acting on sections of .
.
In classical mechanics
, many dynamical system
s are
Lagrangian systems. The configuration space of such a Lagrangian
system is a fiber bundle over the time
over the time
axis (in particular,
(in particular,  if a reference frame is fixed). In classical field theory
if a reference frame is fixed). In classical field theory
, all field systems are the Lagrangian ones.
A Lagrangian density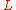 (or, simply, a Lagrangian
(or, simply, a Lagrangian
)
of order is defined as an
is defined as an  -form,
-form,  dim
dim , on the
, on the
 -order jet manifold
-order jet manifold
 of
of  . A Lagrangian
. A Lagrangian 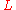 can be introduced
can be introduced
as an element of the variational bicomplex
of the
differential graded algebra
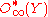 of
of
exterior forms
on jet manifolds
of . The coboundary operator
. The coboundary operator
of this bicomplex
contains the variational operator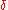 which,
which,
acting on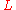 , defines the associated Euler-Lagrange
, defines the associated Euler-Lagrange
operator . Given bundle coordinates
. Given bundle coordinates
 on a fiber bundle
on a fiber bundle  and
and
the adapted coordinates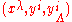
(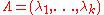 ,
, 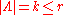 ) on jet manifolds
) on jet manifolds  , a Lagrangian
, a Lagrangian
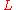 and its Euler-Lagrange operator read
and its Euler-Lagrange operator read
 of a smooth
of a smoothfiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
 and a Lagrangian density
and a Lagrangian density  which yields the Euler-Lagrange differential operator
which yields the Euler-Lagrange differential operatorDifferential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
acting on sections of
 .
.In classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, many dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
s are
Lagrangian systems. The configuration space of such a Lagrangian
system is a fiber bundle
 over the time
over the timeaxis
 (in particular,
(in particular,  if a reference frame is fixed). In classical field theory
if a reference frame is fixed). In classical field theoryClassical field theory
A classical field theory is a physical theory that describes the study of how one or more physical fields interact with matter. The word 'classical' is used in contrast to those field theories that incorporate quantum mechanics ....
, all field systems are the Lagrangian ones.
A Lagrangian density
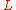 (or, simply, a Lagrangian
(or, simply, a LagrangianLagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
)
of order
 is defined as an
is defined as an  -form,
-form,  dim
dim , on the
, on the -order jet manifold
-order jet manifoldJet bundle
In differential geometry, the jet bundle is a certain construction which makes a new smooth fiber bundle out of a given smooth fiber bundle. It makes it possible to write differential equations on sections of a fiber bundle in an invariant form...
 of
of  . A Lagrangian
. A Lagrangian 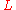 can be introduced
can be introducedas an element of the variational bicomplex
Variational bicomplex
In mathematics, the Lagrangian theory on fiber bundles is globally formulated in algebraic terms of the variational bicomplex, without appealing to the calculus of variations...
of the
differential graded algebra
Differential graded algebra
In mathematics, in particular abstract algebra and topology, a differential graded algebra is a graded algebra with an added chain complex structure that respects the algebra structure.- Definition :...
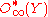 of
ofexterior forms
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
on jet manifolds
Jet bundle
In differential geometry, the jet bundle is a certain construction which makes a new smooth fiber bundle out of a given smooth fiber bundle. It makes it possible to write differential equations on sections of a fiber bundle in an invariant form...
of
 . The coboundary operator
. The coboundary operatorCohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
of this bicomplex
contains the variational operator
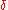 which,
which,acting on
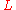 , defines the associated Euler-Lagrange
, defines the associated Euler-Lagrangeoperator
 . Given bundle coordinates
. Given bundle coordinates on a fiber bundle
on a fiber bundle  and
andthe adapted coordinates
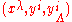
(
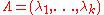 ,
, 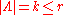 ) on jet manifolds
) on jet manifolds  , a Lagrangian
, a Lagrangian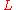 and its Euler-Lagrange operator read
and its Euler-Lagrange operator read-
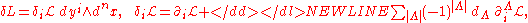
where
-
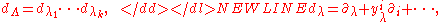
denote the total derivatives. For instance, a first order
Lagrangian and its second-order Euler-Lagrange operator take the
form
-
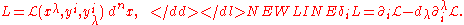
The kernel of an Euler-Lagrange operator provides the
Euler-Lagrange equationEuler-Lagrange equationIn calculus of variations, the Euler–Lagrange equation, Euler's equation, or Lagrange's equation, is a differential equation whose solutions are the functions for which a given functional is stationary...
s .
.
CohomologyCohomologyIn mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
of the variational bicomplex leads to the so called
variational formula
where
-

is the total differential and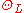 is a Lepage
is a Lepage
equivalent of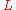 . Noether's first theorem and
. Noether's first theorem and
Noether's second theoremNoether's second theoremIn mathematics, Noether's second theorem relates symmetries of an action functional with a system of differential equations. The action S of a physical system is an integral of a so-called Lagrangian function L, from which the system's behavior can be determined by the principle of least...
are corollaries of this variational
formula.
In a different way, Lagrangians, Euler-Lagrange operators and
Euler-Lagrange equations are introduced in the framework of the
calculus of variationsCalculus of variationsCalculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
.
See also
- LagrangianLagrangianThe Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
- Calculus of variationsCalculus of variationsCalculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
- Noether's theoremNoether's theoremNoether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...
- Noether identitiesNoether identitiesIn mathematics, Noether identities characterize the degeneracy of a Lagrangian system. Given a Lagrangian system and its Lagrangian L, Noether identities can be defined as a differential operator whose kernel contains a range of the Euler–Lagrange operator of L...
- Lagrangian
-
-
-